贵州省铜仁市第一中学2020届高三下学期防疫期间网上测试（二）数学（文）试题 17页

贵州省铜仁一中高三年级防疫期间 ‎“停课不停学”网上测试（二）‎ 文科数学 ‎（‎2020年2月22日 15:00—17:00）‎ 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．设集合，，则（ ）‎ A． B． C． D．‎ ‎2．2．设z＝，则|z|＝(　　)‎ A.2　　　　 　B. C. D.1‎ ‎3．已知向量，，若，则（ ）‎ A． B．‎1 C．2 D．‎ ‎4．函数的大致图象为（ ）‎ A. B． C． D．‎ ‎5.已知等差数列的前项和为，若，，则等差数列的公差（ ）‎ A．2 B． C．3 D．4‎ ‎6．已知定义在区间[－3，3]上的函数f(x)＝2x＋m满足f(2)＝6，在[－3，3]上任取一个实数x，则使得f(x)的值不小于4的概率为(　　)‎ A. B. C. D. ‎7．根据某校10位高一同学的身高(单位：cm)画出的茎叶图（图1），其中左边的数字从左到右分别表示学生身高的百位数字和十位数字，右边的数字表示学生身高的个位数字，设计一个程序框图（图2）， 用表示第个同学的身高，计算这些同学身高的方差， 则程序框图①中要补充的语句是（ ）‎ A． B． ‎ ‎ C． D．‎ ‎8．将函数图象上所有的点向左平行移动个单位长度，再将所得图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），则所得图象对应的函数解析式为（ ）‎ A． B． C． D．‎ ‎9．已知双曲线的左、右焦点分别为，，过作圆的切线，交双曲线右支于点，若，则双曲线的离心率为（ ）‎ A． B．‎2 C． D．‎ ‎10．已知棱长为1的正方体被两个平行平面截去一部分后，剩余部分的三视图如图所示，则剩余部分的表面积为（ ）‎ A． B． C． D．‎ ‎11．已知抛物线上一点到焦点的距离为6，，分别为抛物线与圆上的动点，则的最小值为（ ）‎ A． B． C． D．‎ ‎12．函数恰有两个整数解，则实数的取值范围为（ ）‎ A． B． C． D．‎ 二、填空题：本大题共4小题，每小题5分．‎ ‎13．已知，且，则的值为 ．‎ ‎14．已知变量，满足约束条件，则的最小值为______．‎ ‎15. 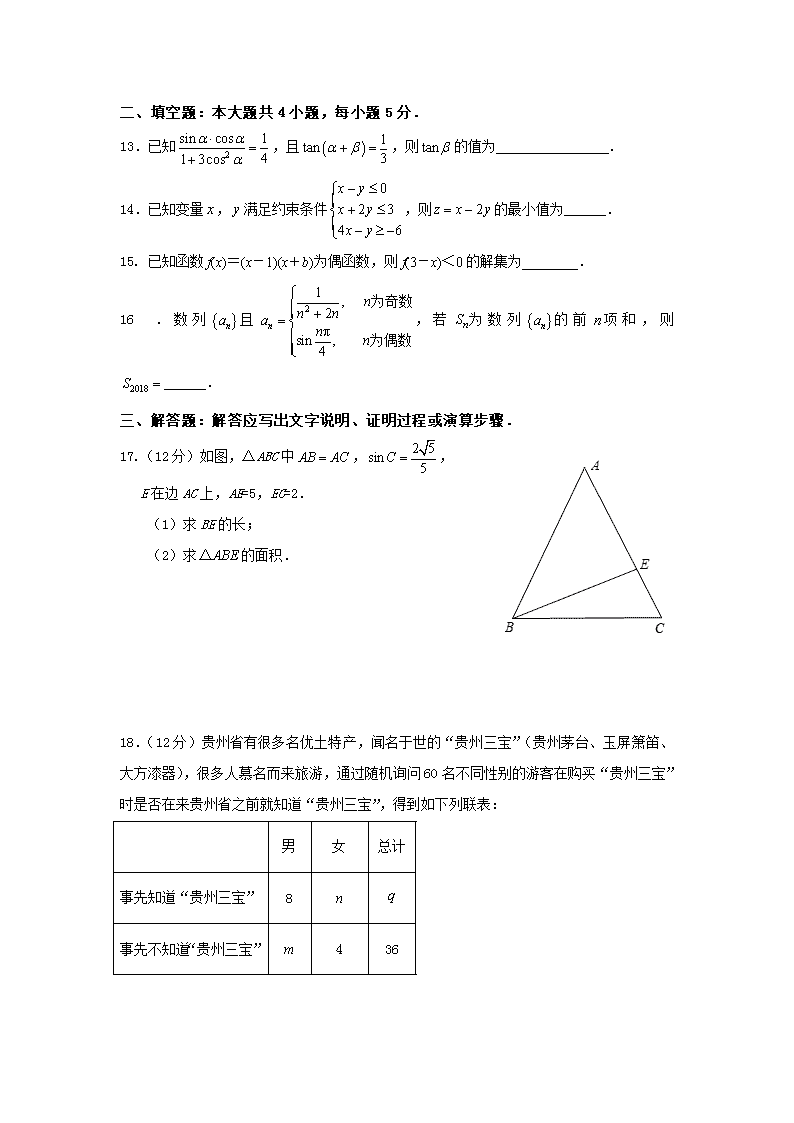已知函数f(x)＝(x－1)(x＋b)为偶函数，则f(3－x)＜0的解集为________．‎ ‎16．数列且，若为数列的前项和，则______．‎ 三、解答题：解答应写出文字说明、证明过程或演算步骤．‎ ‎17.（12分）如图，△ABC中，，‎ E在边AC上，AE=5，EC=2．‎ ‎（1）求BE的长；‎ ‎（2）求的面积．‎ ‎18．（12分）贵州省有很多名优土特产，闻名于世的“贵州三宝”（贵州茅台、玉屏箫笛、大方漆器），很多人慕名而来旅游，通过随机询问60名不同性别的游客在购买“贵州三宝”时是否在来贵州省之前就知道“贵州三宝”，得到如下列联表：‎ 男 女 总计 事先知道“贵州三宝”‎ ‎8‎ 事先不知道“贵州三宝”‎ ‎4‎ ‎36‎ 总计 ‎40‎ 附：，‎ ‎（1）写出列联表中各字母代表的数字；‎ ‎（2）由以上列联表判断，能否在犯错误的概率不超过的前提下认为购买“贵州三宝”和是否“事先知道‘贵州三宝’有关系”？‎ ‎19．（12分）如图所示，在四棱锥PABCD中，∠CAD＝∠ABC＝90°，∠BAC＝∠ADC＝30°，PA⊥平面ABCD，E为PD的中点，AC＝2.‎ ‎(1)求证：AE∥平面PBC；‎ ‎(2)若四面体PABC的体积为，求△PCD的面积.‎ ‎20．（12分）已知椭圆经过点，且右焦点．‎ ‎（1）求椭圆的方程；‎ ‎（2）若直线与椭圆交于，两点，当最大时，求直线的方程．‎ ‎21．（12分）已知函数在处的切线与直线平行．‎ ‎（1）求实数的值，并判断函数的单调性；‎ ‎（2）若函数有两个零点，，且，求证：．‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．‎ ‎22.（10分）在直角坐标系中，曲线的参数方程为，（为参数）．以原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为．‎ ‎（1）求曲线的普通方程和的直角坐标方程；‎ ‎（2）已知曲线的极坐标方程为，点是曲线与的交点，点是曲线与的交点，且，均异于极点，且，求实数的值．‎ ‎23．（10分）【选修4-5：不等式选讲】‎ 若，，且．‎ ‎（1）求的最小值；‎ ‎（2）是否存在，，使得的值为？并说明理由．‎ 贵州省铜仁一中高三年级防疫期间 ‎“停课不停学”网上测试（二）‎ 数学文科答题卡 班级 姓名 得分 ‎ 一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的 ‎1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.‎ 二、填空题：本题共4小题，每小题5分，共20分.‎ ‎1 ________ ． 2_______. 3______． 4______．‎ 三、解答题共70分．解答应写出文字说明，证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．‎ ‎17．‎ ‎18、‎ ‎19. ‎ ‎ 20. ‎ ‎21．‎ 选考题：共10分.请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分.‎ ‎22.‎ ‎23．‎ 贵州省铜仁一中高三年级防疫期间 ‎“停课不停学”网上测试（二）‎ 文科数学参考答案 评分说明：‎ ‎1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制定相应的评分细则.‎ ‎2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分.‎ ‎3．解答右端所注分数，表示考生正确做到这一步应得的累加分数.‎ ‎4．只给整数分数.选择题和填空题不给中间分.‎ 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．A。解不等式，得，即，由，得，即，所以，‎ ‎2．C。　法一：∵ z＝＝＝，∴ |z|＝ ＝.‎ 法二：|z|＝＝＝＝.‎ ‎3.B。由题意，，，，解得．‎ ‎4．D。，排除B，C，当时，，则时，，，排除A。‎ ‎5.C。依题意有，解之得。‎ ‎6．B。　∵f(2)＝6，∴22＋m＝6，解得m＝2.‎ 由f(x)≥4，得2x＋2≥4，即x≥1，而x∈[－3，3]，‎ 故根据几何概型的概率计算公式，得f(x)的值不小于4的概率P＝＝.‎ ‎7．B。由 ‎，‎ 循环退出时，知．∴，‎ 故程序框图①中要补充的语句是 ‎8．A。先将函数图象上所有的点向左平行移动个单位长度，‎ 得，再将所得图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），得。‎ ‎9．A。如图，设切点为，连接，过作，‎ 垂足为，由，且为的中位线，得，，即有，在直角三角形中，‎ 得，即有，双曲线的定义可得，可得，‎ 所以，所以。‎ ‎10.B。由三视图可得，该几何体为如图所示的正方体截去三棱锥和三棱锥后的剩余部分．其表面为六个腰长为1的等腰直角三角形和两个边长为的等边三角形，所以其表面积为 ‎ 11.D 。由抛物线焦点在轴上，准线方程，则点到焦点的距离为，则，所以抛物线方程，设，圆，圆心为，半径为1，‎ 则，当时，取得最小值，最小值为，‎ ‎12． D。函数恰有两个整数解，即恰有两个整数解，令，得，令，易知为减函数．当，，，单调递增；当，，，单调递减．，，．‎ 由题意可得：，∴．‎ 二、填空题：本大题共4小题，每小题5分．‎ ‎13．‎ ‎∵，∴，‎ 又，解得．故答案为．‎ ‎14.‎ 画出，满足的可行域，‎ 由，解得，‎ 当目标函数经过点时，‎ 取得最小值为．‎ ‎15. (2，4)‎ 解析：由函数f(x)＝x2＋(b－1)x－b是偶函数，得b－1＝0，b＝1，f(x)＝x2－1.f(3－x)＜0，即(3－x)2－1＜0，解得2＜x＜4.因此，不等式f(3－x)＜0的解集是(2，4).‎ ‎16．‎ 数列且，当为奇数时，；‎ 当为偶数时，，所以，‎ ‎．‎ 三、解答题：解答应写出文字说明、证明过程或演算步骤．‎ ‎17.‎ ‎18．（1）由列联表能求出，，，，．………………6分 ‎（2）由计算可得，所以在犯错误的概率不超过的前提下，认为购买“贵州三宝”和“事先知道‘贵州三宝’有关系”. …………12分 ‎19．(1)证明：如图，取CD的中点F，连接EF，AF，则EF∥PC，‎ 又易知∠BCD＝∠AFD＝120°，∴AF∥BC，‎ 又EF∩AF＝F，PC∩BC＝C，∴平面AEF∥平面PBC.‎ 又AE⊂平面AEF，∴AE∥平面PBC. ………………6分 ‎(2)由已知得，V四面体PABC＝·AB·BC·PA＝，可得PA＝2.‎ 过A作AQ⊥CD于Q，连接PQ，在△ACD中，AC＝2，∠CAD＝90°，∠ADC＝30°，‎ ‎∴CD＝4，AD＝2，AQ＝＝，则PQ＝ ＝.∵PA⊥平面ABCD，∴PA⊥CD.‎ 又AQ∩PA＝A，∴CD⊥平面PAQ，CD⊥PQ.∴S△PCD＝×4×＝2.………………12分 20． ‎（1）设椭圆的左焦点，则，‎ 又，所以椭圆的方程为．………………6分 ‎（2）由，设，，………8分 由，且，，‎ ‎．‎ 设，则，，‎ 当，即时，有最大值，此时．………………12分 ‎21．（1）函数的定义域：，，解得，………………2分 ‎∴，∴，‎ 令，解得，故在上是单调递减；‎ 令，解得，故在上是单调递增．………………6分 ‎（2）由，为函数的两个零点，得，，两式相减，可得，即，，因此，，‎ 令，由，得．则，构造函数， ‎ 则，∴函数在上单调递增，故，即，可知．‎ 故命题得证．………………12分 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．‎ ‎22.（1），．………………5分 ‎（2），联立极坐标方程，得，，‎ ‎，，，∴或．…10分 ‎23．（1），，，，，当且仅当时取等号，‎ ‎，．，‎ ‎，当且仅当时取等号．………………5分 （2） ‎，，，‎ ‎，‎ 不存在，，使得的值为．………………10分