2019届二轮（理科数学） 小题易丢分 作业（江苏专用） 17页

‎2019届二轮（理科数学） 小题易丢分 作业（江苏专用）‎ 一、填空题 ‎1．已知，又（），若满足的有三个，则的取值范围是__________．‎ ‎【答案】‎ ‎【解析】 由题意得， ，‎ 当时，当时， ‎ 设，则 ‎ 要使得有三个不同的零点，则方程有两个不同的根，‎ 其中一个根在之间，一个根在之前，即 且 设 ，则，‎ 即实数的取值范围是.‎ 考点：函数与方程的应用.‎ 点睛：本题主要考查了函数与方程问题，其中解答中涉及到函数的零点问题的求解，分段函数的性质，一元二次函数的图象与性质点应用问题，着重考查了学生分析问题和解答问题的能力，以及推理与运算能力，本题的解答中根据函数的值域，转化为一元二次方程根的分布是解答问题的关键.‎ ‎2．下列说法正确的是___________． ‎ ‎①任意，都有； ②函数 有三个零点；‎ ‎③的最大值为； ④函数为偶函数；‎ ‎⑤函数的定义域为[1，2 ，则函数y=f（2x）的定义域为[2，4 ．‎ ‎【答案】②③‎ ‎【解析】‎ ‎【分析】‎ ‎①对赋值判断其错误。②作出与的图像，由图可知函数 有三个零点。③由指数函数的单调性可知其正确。④对赋值判断其错误。⑤对赋值可判断其错误。‎ ‎【详解】‎ ‎①当时，不等式不成立。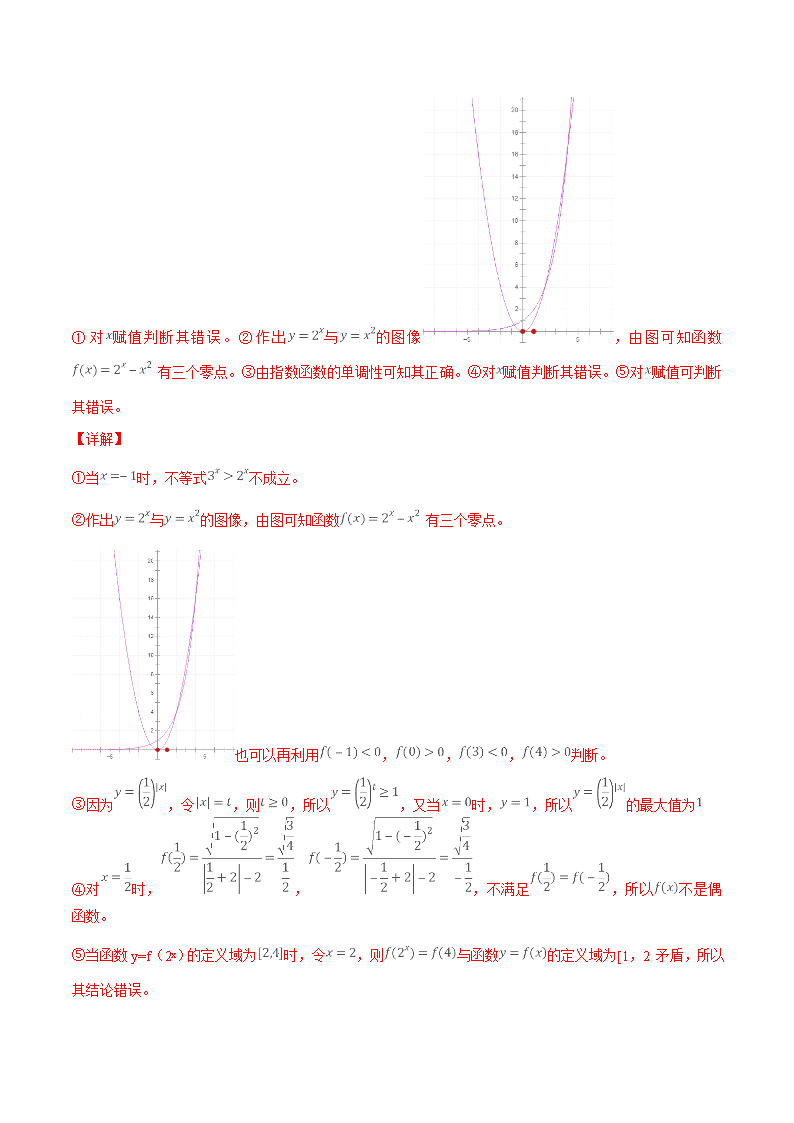‎ ‎②作出与的图像，由图可知函数 有三个零点。‎ 也可以再利用，，，判断。‎ ‎③因为，令，则，所以，又当时，，所以的最大值为 ‎④对时，，，不满足，所以不是偶函数。‎ ‎⑤当函数y=f（2x）的定义域为时，令，则与函数的定义域为[1，2 矛盾，所以其结论错误。‎ ‎【点睛】‎ 对于错误的结论，只需要找到一个不满足要求的反例即可，考查了比较大小关系，函数零点个数问题，最值，奇偶性及抽象函数定义域问题。‎ ‎3．已知是两个不共线的非零向量，且与 起点相同．若，，三向量的终点在同一直线上，则________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 利用向量共线基本定理得出+，化简(λ−)+(t−λt−)=，由是两个不共线的非零向量得出系数分别为0，构造方程组，即可解出t ‎【详解】‎ 设+，‎ 化为(λ−)+(t−λt−)=，‎ ‎∵是两个不共线的非零向量，且与 起点相同，‎ ‎∴λ−, t−λt−解得λ=,t=.‎ ‎∴当t=时,，，三向量的终点在同一直线上。‎ ‎【点睛】‎ 本题主要考察向量共线基本定理，首先根据向量三角形法则表示出在同一条直线上任意两向量，然后运用向量共线条件去解决问题。‎ ‎4．已知函数的定义域为,若对于 、、分别为某个三角形的边长，则称为“三角形函数”。给出下列四个函数：‎ ‎①； ②；‎ ‎③；④.‎ 其中为“三角形函数”的数是_____.‎ ‎【答案】①④‎ ‎【解析】分析：分析题意，先由 、、分别为某个三角形的边长，得到、、‎ 满足三角形的三边关系，之后逐个对函数的值域进行分析求解，从而得到结果.‎ 详解：对于①，，对于 、、 ，所以分别为某个三角形的边长，故①是“三角形函数”；‎ 对于②， ，当时，不满足三角形的三边关系，故②不是“三角形函数”；‎ 对于③，，当时，不满足三角形的三边关系，故③不是“三角形函数”；‎ 对于④， ,‎ 令，此时有 ，所以分别为某个三角形的边长，故④是“三角形函数”；‎ 故答案是①④.‎ 点睛：该题考查的是有关新定义的问题，在解题的过程中，注意对新定义的正确理解，注意三角形三边的关系，结合所给函数的值域，进行分析，得到结果.‎ ‎5．设函数的定义域为，若对于任意，当时，恒有，则称点为函数图象的对称中心.研究函数的某一个对称中心，并利用对称中心的上述定义，可得到 的值为__________．‎ ‎【答案】‎ ‎【解析】当时， ，的对称中心为，， ，故答案为.‎ ‎6．已知, 则的取值范围是________.‎ ‎【答案】‎ ‎7．对a，，设，函数若关于x的方程有两个不同的实数解，则实数 的取值范围是______．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 由最小值的定义，解不等式即可得到f（x）的分段函数形式，作出图象，以及直线y= x﹣1，通过直线绕（0，﹣1）旋转，即可得到所求范围．‎ ‎【详解】‎ 当，即，则；‎ 当时，．‎ 即有，‎ 作出函数的图象，以及直线，‎ 由直线绕着点旋转，可得时，‎ 的图象与直线有两个交点，学 ‎ 故答案为：‎ ‎【点睛】‎ 本题考查函数的零点个数问题，注意运用转化思想和数形结合思想，考查化简运算能力，属于中档题．‎ ‎8．已知函数其中，若函数的图象上恰好有两对关于y轴对称的点，则实数的取值范围为____．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 转化函数的图象上恰好有两对关于轴对称的点，就是时，与，有两个交点，利用函数的零点列出不等式，转化求解即可．‎ ‎【详解】‎ 已知函数其中，若函数的图象上恰好有两对关于y轴对称的点， 即时，与，有两个交点，恒过（1，0），中是函数的零点，所以必须满足， 解得 ． 故答案为：．‎ ‎【点睛】 学 ‎ 本题考查函数的零点个数的判断，考查转化思想的应用，属中档题.．‎ ‎ 9．已知锐角满足，当取得最大值时， _________.‎ ‎【答案】‎ ‎【解析】由题意可知： ，‎ ‎∴ . ‎ ‎∴.‎ ‎.‎ 当α取得最大值时, 取得最大. ，‎ 当时, 有最大值为.‎ ‎∴.学 ‎ 故答案为： .‎ ‎10．已知点， ， 是曲线上一个动点，则的最大值是__________．‎ ‎【答案】‎ ‎ 11．若（， ）对任意实数都有.记，则__________．‎ ‎【答案】‎ ‎【解析】对于任意实数，都有， ‎ 函数的图象关于直线对称，故有 为最大值或最小值，即 ,故有，故答案为.‎ ‎12．已知为的外接圆圆心， ， ，若，且，则__________．‎ ‎【答案】10 . ‎ ‎ 13．化简的值为__________．‎ ‎【答案】‎ ‎【解析】原式 ‎ ‎，故答案为.‎ ‎14．设函数 (其中是常数)．若函数在区间上具有单调性，且，则的对称中心坐标为（_______________），0）（其中）.‎ ‎【答案】‎ ‎ 15．给出下列命题：①存在实数，使；②若是第一象限角，且，则；③函数是奇函数；④函数的周期是；⑤函数的图象与函数（）的图像所有交点的横坐标之和等于6．‎ 其中正确命题的序号是______（把正确命题的序号都填上）‎ ‎【答案】⑤‎ ‎ 16．已知则=__________.‎ ‎【答案】‎ ‎【解析】 . ‎ 而 ，‎ ‎ ， ，故答案为.‎ ‎17．设x∈R，f(x)＝，若不等式f(x)＋f(2x)≤ 对于任意的x∈R恒成立，则实数 的取值范围是________．‎ ‎【答案】 ≥2 ‎ ‎【解析】不等式化为 ≥＋的最大值，因为∈(0，1 ，所以 ≥2.‎ 点睛：对于求不等式成立时的参数范围问题，在可能的情况下把参数分离出来，使不等式一端是含有参数的不等式，另一端是一个区间上具体的函数，这样就把问题转化为一端是函数，另一端是参数的不等式，便于问题的解决.但要注意分离参数法不是万能的，如果分离参数后，得出的函数解析式较为复杂，性质很难研究，就不要使用分离参数法.‎ ‎18．如图，点是正六边形的边上的一个动点，设，则的最大值为______．‎ ‎ . ‎ ‎【答案】2‎ ‎ 19．设是定义在上的奇函数，且，设，若函数有且只有一个零点，则实数t的取值范围是__________．‎ ‎【答案】‎ ‎【解析】‎ ‎ 是定义在 上的奇函数，且 ，即 ，得 ，则 ‎ ， ，则当 时，函数为增函数，且当 时， ，当 时，函数为减函数，且 ,由 得 ，作出函数 和 的图象如图：要使函数 有且只有一个零点，则函数 与只有一个交点，则 ，故答案为 .‎ ‎20．已知为的外心， ， ，如果，其中、满足，则_________.‎ ‎【答案】‎ ‎ 21．若函数能够在某个长度为1的闭区间上至少两次获得最大值1，且在区间上为增函数，则正整数的值为__________．‎ ‎【答案】7‎ ‎【解析】由题意得：，又由在区间上为增函数得，所以正整数的值为 ‎22．已知函数在上为增函数，则的取值范围是__________．‎ ‎【答案】‎ ‎ 23．已知函数和，若存在实数使得，则实数的取值范围为__________．‎ ‎【答案】‎ ‎【解析】‎ 当时, ‎ ‎;当时,,若存在使,则,即,解得,故填.‎ 点睛：本题考查学生的是函数的应用问题,属于中档题目.首先求出分段函数的值域,一段根据对数函数的单调性,另外一段利用对勾函数的性质以及基本不等式和反比例的值域求得,根据题意,即方程有解问题,从而限制的范围,解出不等式即可.‎ ‎24．如图所示，在中，点是的中点，过点的直线分别交直线，于不同的两点，，若，，则的值为__________．‎ ‎【答案】 ‎ ‎【解析】 . ‎ 由题意得 ,所以. ‎ ‎25．当直线y＝ (x－2)＋4和曲线y＝有公共点时，实数 的取值范围是________．‎ ‎【答案】‎ ‎ 26．已知函数，若关于x的方程f（x）﹣ =0有唯一一个实数根，则实数 的取值范围是 ．‎ ‎【答案】[0，1）∪（2，+∞）‎ ‎【解析】‎ 试题分析：关于x的方程f（x）- =0有唯一一个实数根，‎ 等价于函数y=f（x）与y= 的图象有唯一一个交点，‎ 在同一个坐标系中作出它们的图象可得：‎ 由图象可知实数 的取值范围是[0，1）∪（2，+∞）‎ 考点：函数的零点 ‎27．已知θ∈（，），若存在实数x，y同时满足=，+=，则tanθ的值为 ．‎ ‎【答案】‎ 把②代入①，化简得+=③；‎ 又tanθ==，‎ 所以③式化为tan2θ+=，‎ 解得tan2θ=2或tan2θ=；‎ 所以tanθ=±或tanθ=±；‎ 又θ∈（，），‎ 所以tanθ＞1，‎ 所以取tanθ=． . ‎ 故答案为：．‎ ‎28．已知函数是定义域为的偶函数. 当时， ，则f(1)= 若关于的方程（）,有且仅有6个不同实数根，则实数的取值范围是 ‎ ‎【答案】 ； ‎ ‎ . ‎ 关于x的方程，解得，当时，，当时，，由，则有4个实根，于是由图像可得，当时，有两个实根，当时，有两个实根，综上可得，‎ 考点：分段函数的应用及函数奇偶性和根的存在性以及根的分布 ‎29．已知函数f（x）满足f（x﹣1）=﹣f（﹣x+1），且当x≤0时，f（x）=x3，若对任意的x∈[t，t+2 ，不等式f（x+t）≥2f（x）恒成立，则实数t的取值范围是 ．‎ ‎【答案】[，+∞）‎ 则t≥=，‎ 故实数t的取值范围[，+∞），‎ 故答案为：[，+∞）‎ 考点：函数恒成立问题；抽象函数及其应用．‎ ‎30．已知函数f（x）=sinx．若存在x1，x2，…，xm满足0≤x1＜x2＜…＜xm≤6π，且 f（x1）﹣f（x2） + f（x2）﹣f（x3） +…+ f（xm﹣1）﹣f（xm） =12（m≥0，m∈N ），则m的最小值为 ．‎ ‎【答案】8‎