山东省济宁市曲阜市第一中学2019-2020学年高二下学期期中线上考试数学试卷 12页

数学科试题 第Ⅰ卷（共 60 分）‎ 注意事项：考试结束后，及时上传答卷 一、单项选择题：本题共 8 小题，每小题 5 分，共 40 分。在每小题给出的四个选项中，只有一项符合题目要求的。‎ ‎1. 已知集合 A = {x | y = 1- 2x} ， B = {x | y = lg(2x -1)} ，则 等于（ ）‎ ‎}‎ A．{x | 0 £ x < 1‎ ‎2‎ ‎B．{x | 0 < x < 1‎ ‎}‎ ‎2‎ ‎C．{x | 0 £ x £ 1‎ ‎}‎ ‎2‎ ‎D．{x | 0 < x £ 1‎ ‎}‎ ‎2‎ ‎2. 命题“ "x Î R, x3 - x2 + 1 £ 0 ”的否定是（ ）‎ o o o A．存在 x Î R, x 3 - x 2 +1 > 0‎ o o o C. 不存在 x Î R, x 3 - x 2 +1 £ 0‎ ‎B．存在 x Î R, x 3 - x 2 +1 £ 0‎ o o o D. 对任意的"x Î R, x3 - x2 + 1 > 0‎ ‎＝‎ ‎，则方差 3. 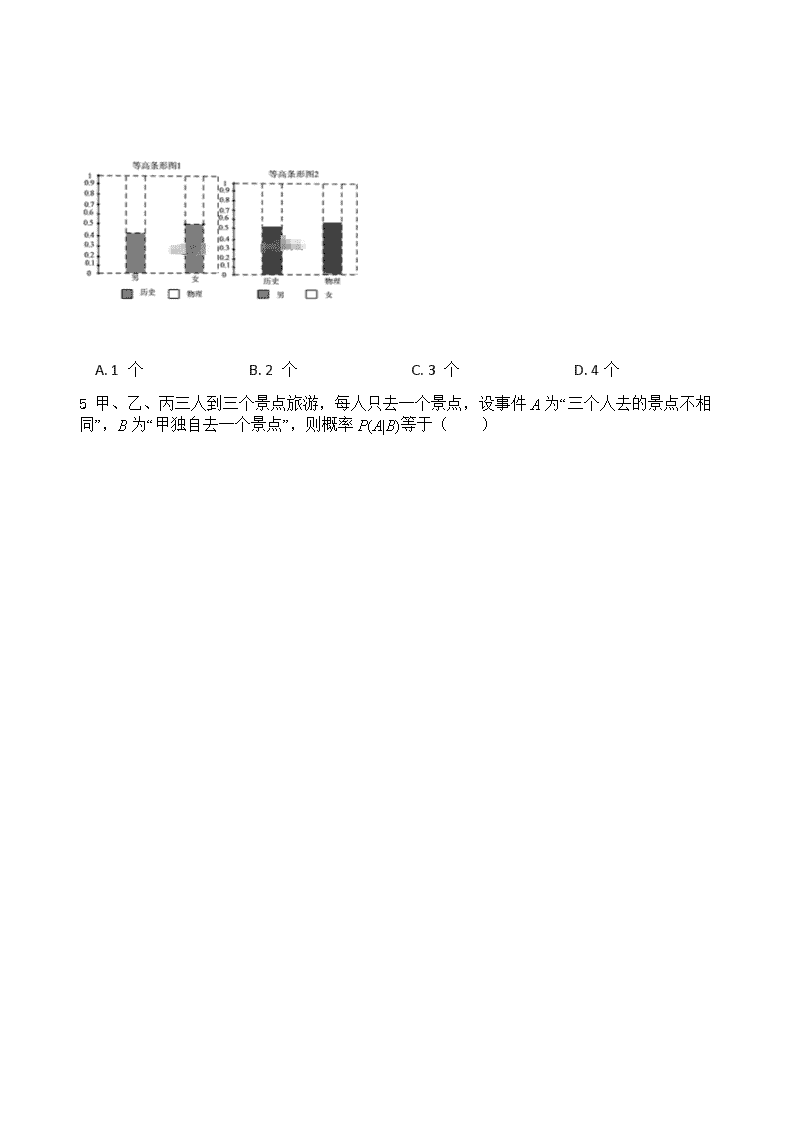设随机变量 X 服从二项分布，且均值 E(X)＝3，p 1‎ ‎D(X)＝（ ）‎ ‎5‎ A 3 4 12‎ ‎． B．‎ ‎5 5‎ ‎C． 5‎ ‎D．2‎ 4. 新高考科目设置采用新模式，普通高中学生从高一升高二时将面临着选择物理还是历史的问题，某校抽取了部分男、女学生调查选科意向，制作出如下图所示的等高条形图，现给出下列结论：‎ ‎①样本中的女生更倾向于选历史；‎ ‎②样本中的男生更倾向于选物理；‎ ‎③样本中的男生和女生数量一样多；‎ ‎④样本中意向物理的学生数量多于意向历史的学生数量.‎ 根据两幅条形图的信息，可以判断上述结论正确的有（ ）‎ A. 1 个 B. 2 个 C. 3 个 D. 4 个 3. 甲、乙、丙三人到三个景点旅游，每人只去一个景点，设事件 A 为“三个人去的景点不相同”，B 为“甲独自去一个景点”，则概率 P(A|B)等于（ ）‎ A 4 B 2 C 1 D 1‎ ‎． ． ． ．‎ ‎9 9 2 3‎ ‎6. 设 x ÎR ，则“| x - 2 |< 1”是“ x2 + 2x - 3 > 0 ”的（ ）‎ A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 7. ‎《红海行动》是一部现代海军题材影片，该片讲述了中国海军“蛟龙突击队”奉命执行撤侨任务的故事．撤侨过程中，海军舰长要求队员们依次完成六项任务，并对任务的顺序提出了如下要求：重点任务 A 必须排在前三位，且任务 E 、F 必须排在一起，则这六项任务的不同安排方案共有（ ）‎ A．240 种 B．188 种 C．156 种 D．120 种 ex - e- x 8. 已知函数 f (x) = ex + e- x ，实数m, n 满足不等式 f (2m - n) + f (2 - n) > 0 ，则下列不等关系 成立的是（ ）‎ A. m + n >1‎ ‎B. m + n <1‎ ‎C. m - n > -1‎ ‎D. m - n < -1‎ 二、多项选择题：本题共 4 小题，每小题 5 分，共 20 分。在每小题给出的选项中，有多项 符合题目要求。全部选对的得 5 分，有选错的得 0 分，部分选对的得 3 分。‎ 9. 研究变量 x, y 得到一组样本数据，进行回归分析，以下说法正确的是（ ）‎ A. 残差平方和越小的模型，拟合的效果越好；‎ B. 用相关指数 R2 来刻画回归效果， R2 越小说明拟合效果越好；‎ C. 在回归直线方程 yˆ = 0.2x + 0.8 中,当解释变量 x 每增加 1 个单位时,预报变量 yˆ 平均增加 0.2 个单位；‎ D. 若变量 y 和 x 之间的相关系数为 r = -0.9462 ，则变量 y 和 x 之间的负相关很弱.‎ ‎10.若 (1+ mx)8 = a + a x + a x2 + L+ a x8 且 a + a ‎+L+ a ‎= 255 ，则实数 m 的值可以为 ‎0 1 2 8‎ ‎（ ）‎ ‎1 2 8‎ A．0 B．-1 C．-3 D．1‎ ‎11．如图是 2018 年第一季度五省 GDP 情况图，则下列陈述中正确的是( )‎ A.2017 年同期 A 省的 GDP 总量也是第三位．‎ B.与去年同期相比，2018 年第一季度五个省的 GDP 总量均实现了增长； C.去年同期的 GDP 的总量前三位是 D 省、B 省、A 省；‎ D.2018 年第一季度 GDP 总量和增速均居同一位的省只有 1 个；‎ ‎12.已知函数 （f x）对"x Î R ，满足 f (x) = - f (6 - x), f (x +1) = f (-x +1) ，若 f (a) = - f (2020), a Î[5,9]且 f（x）在［5，9］上为单调函数，则下列结论正确的是（ ）‎ A. ‎（f ‎3）=0 B．‎ ‎a = 8‎ C． （f x）是周期为 4 的周期函数 D． y＝（f x）的图象关于点(1, 0) 对称 第Ⅱ卷（非选择题 共 90 分）‎ 三、13、填空题：本大题共 4 小题，每小题 5 分，共 20 分。‎ ‎（1）.若随机变量 X 的分布列如下表，且 E(X ) = 2 ，则 D(2 X - 3) 的值为 ．‎ ‎（2）. æ 1 -1ö( +1)5 展开式中 x 的系数为 .‎ x ç ÷ è ø x2＋2x＋3‎ ‎（3）．函数 y＝‎ ‎x－1‎ ‎(x>1)的值域是 ．‎ ìï 2x -1, x < 1,‎ f (x) = í ‎（4）.已知函数 ïî2 - x, x ³ 1,‎ ‎‎ 若0 £ ‎‎ f (x) £ 1, 则 x 的取值范围是 ；若关于 x 的函 数 y = f 2 (x) + 2bf (x) + 2b +1有 6 个不同的零点，则实数b 的取值范围是 ．‎ ‎（本题第一空 2 分，第二空 3 分）‎ 四、解答题：本大题共 6 小题，共 70 分。解答应写出文字说明、证明过程或演算步骤。‎ ‎14.（本小题满分 10 分）‎ 已知函数 f ( x ) = 1 x3 - ax + 1(a Î R)，f ¢(x ) 是 f ( x ) 的导函数，且 f ¢(2) = 0 ．‎ ‎3‎ （1） 求a 的值；‎ （2） 求函数 f ( x ) 在区间[-3, 3] 上的最值．‎ ‎15. （本小题满分 12 分）‎ 在一次元旦晚会上，有 6 个演唱节目，4 个舞蹈节目.‎ ‎①当 4 个舞蹈节目要排在一起时，有多少种不同的节目安排顺序？‎ ‎②当要求每 2 个舞蹈节目之间至少安排 1 个演唱节目时，有多少种不同的节目安排顺序？‎ ‎③若已定好节目单，后来情况有变，需加上诗朗诵和快板 2 个节目，但不能改变原来节目的相对顺序，有多少种不同的节目演出顺序？‎ ‎16.（本小题满分 12 分）‎ ç ‎（Ⅰ）若æ ax2 + è ‎b ö6‎ ÷ x ø ‎‎ 的展开式中 x3 项的系数为 20，求 a2 + b2 的最小值.‎ ‎（Ⅱ）已知 (1 + x) + (1 + x)2 +L+ (1 + x)n = a + a x + a x2 +L+ a xn ，‎ 若 a1 + a2 +L + an-1 = 29 - n，求 n ．‎ ‎0 1 2 n ‎17.（本小题满分 12 分）（12 分）‎ 得分 ‎[30,40)‎ ‎[40,50)‎ ‎[50,60)‎ ‎[60,70)‎ ‎[70, 80)‎ ‎[80,90)‎ ‎[90,100]‎ 男性人 ‎40‎ ‎90‎ ‎120‎ ‎130‎ ‎110‎ ‎60‎ ‎30‎ 女性人 ‎20‎ ‎50‎ ‎80‎ ‎110‎ ‎100‎ ‎40‎ ‎20‎ 推进垃圾分类处理，是落实绿色发展理念的必然选择，也是打赢污染防治攻坚战的重要环节.为了解居民对垃圾分类的了解程度，某社区居委会随机抽取1000 名社区居民参与问卷测试，并将问卷得分绘制频率分布表如下：‎ （1） 从该社区随机抽取一名居民参与问卷测试，试估计其得分不低于60 分的概率；‎ 不太了解 比较了解 男性 女性 （2） 将居民对垃圾分类的了解程度分为“比较了解”‎ ‎（得分不低于 60 分）和“不太了解”（得分低于 60 分）两类，完成2 ´ 2 列联表，并判断是否有95% 的把握认为“居民对垃圾分类的了解程度”与“性别” 有关?‎ （3） 从参与问卷测试且得分不低于80 分的居民中，按照性别进行分层抽样，共抽取10‎ 人，连同n (n Î N*) 名男性调查员一起组成3 个环保宣传队.若从这n + 10 人中随机抽取3 人作为队长，且男性队长人数x的期望不小于 2，求 n 的最小值.‎ 附： K 2‎ ‎= n(ad - bc)2‎ ‎(a + b)(c + d )(a + c)(b + d )‎ ‎, (n = a + b + c + d ) .‎ 临界值表：‎ P(K 2 ³ k )‎ ‎0‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k0‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎18.（本小题满分 12 分）公元 2020 年春，我国湖北武汉出现了新型冠状病毒，人感染后会出现发热、咳嗽、气促和呼吸困难等，严重的可导致肺炎甚至危及生命.为了尽快遏制住病毒的传播，我国科研人员，在研究新型冠状病毒某种疫苗的过程中，利用小白鼠进行科学试验.为了研究小白鼠连续接种该疫苗后出现 Z 症状的情况，决定对小白鼠进行做接种试验.该试验的设计为：‎ ‎①对参加试验的每只小白鼠每天接种一次；②连续接种三天为一个接种周期；‎ ‎③试验共进行 3 个周期.‎ 已知每只小白鼠接种后当天出现 Z 症状的概率均为 1‎ ‎4‎ 与上次接种无关.‎ ‎，假设每次接种后当天是否出现 Z 症状 ‎（Ⅰ）若某只小白鼠出现 Z 症状即对其终止试验，求一只小白鼠至多能参加一个接种周期试验的概率；‎ ‎（Ⅱ）若某只小白鼠在一个接种周期内出现 2 次或 3 次 Z 症状，则在这个接种周期结束后， 对其终止试验.设一只小白鼠参加的接种周期数为 X，求 X 的分布列及数学期望.‎ x ‎2‎ ‎3‎ ‎4‎ ‎6‎ ‎8‎ ‎10‎ ‎13‎ ‎21‎ ‎22‎ ‎23‎ ‎24‎ ‎25‎ y ‎13‎ ‎22‎ ‎31‎ ‎42‎ ‎50‎ ‎56‎ ‎58‎ ‎68.5‎ ‎68‎ ‎67.5‎ ‎66‎ ‎66‎ ‎19. （本小题满分 12 分）某汽车公司拟对“东方红”款高端汽车发动机进行科技改造，根据市场调研与模拟，得到科技改造投入 x （亿元）与科技改造直接收益 y （亿元）的数据统计如下：‎ 当0 < x £ 16 时，建立了 y 与 x 的两个回归模型：模型①： yˆ = 4.1x +11.8 ；模型②：‎ yˆ = 21.3 -14.4 ；当 x > 16 时，确定 y 与 x 满足的线性回归方程为： yˆ = -0.7x + a ．‎ ‎（Ⅰ）根据下列表格中的数据，比较当0 < x £ 16 时模型①、②的相关指数 R2 ，并选择拟合 精度更高、更可靠的模型，预测对“东方红”款汽车发动机科技改造的投入为16 亿元时的直接收益．‎ 回归模型 模型①‎ 模型②‎ 回归方程 yˆ = 4.1x +11.8‎ yˆ = 21.3 x -14.4‎ ‎7‎ å( y - yˆ )2‎ i i i=1‎ ‎182.4‎ ‎79.2‎ n å( y - yˆ )2‎ i i n ‎（附：刻画回归效果的相关指数 R2 = 1- i=1 ．）‎ å( yi - y )‎ ‎2‎ i=1‎ ‎（Ⅱ）为鼓励科技创新，当科技改造的投入不少于20 亿元时，国家给予公司补贴收益10 亿元，以回归方程为预测依据，比较科技改造投入16 亿元与20 亿元时公司实际收益的大小；‎ ‎（附：用最小二乘法求线性回归方程 yˆ = bˆx + aˆ 的系数公式 n n ‎ å xi yi - nx × y å(xi - x)( yi - y) ‎ n n ‎ bˆ = i=1 = i=1 ; aˆ = y - bˆx ）‎ å x 2 - nx 2 å(x - x)2‎ i i i=1 i=1‎ ‎（Ⅲ）科技改造后，“东方红”款汽车发动机的热效率X 大幅提高，X 服从正态分布N (0.52, 0.012 ) ,‎ 公司对科技改造团队的奖励方案如下：若发动机的热效率不超过50% ，不予奖励；若发动机的热效率超过50% 但不超过53% ，每台发动机奖励2 万元；若发动机的热效率超过53% ，每台发动机奖励4 万元．求每台发动机获得奖励的分布列和数学期望．‎ ‎（附：随机变量x服从正态分布 N (m,s2 ) ，则 P(m-s< x< m+s) = 0.6827 ，‎ P(m- 2s< x< m+ 2s) = 0.9545 ．）‎