浙江省金兰教育合作组织2019-2020学年高一上学期期中考试数学试题 16页

www.ks5u.com 浙江金兰教育合作组织2019-2020年度第一学期高一数学期中考试试卷 一、选择题（本大题共10小题）‎ ‎1.已知集合，则 A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ 试题分析：由得，所以，因为，所以，故选D.‎ ‎【考点】 一元二次不等式的解法，集合的运算 ‎【名师点睛】对于集合的交、并、补运算问题，应先把集合化简再计算，常常借助数轴或韦恩图处理.‎ ‎2.幂函数f（x）=k•的图象过点，则k+=（　　）‎ A. B. 1 C. D. 2‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 由函数f（x）=k•xα是幂函数，根据幂函数的定义可知，其系数k=1，再将点的坐标代入可得值，从而得到幂函数的解析式．‎ ‎【详解】∵函数f（x）=k•xα是幂函数，‎ ‎∴k=1，‎ ‎∵幂函数f（x）=xα的图象过点，‎ ‎∴（）α=，得=，‎ 则k+=1+=．‎ 故选：C．‎ ‎【点睛】本题考查幂函数的定义及图象与性质，属于基础题．‎ ‎3.若a=20.3，b=logπ3，c=log40.3，则（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 利用对数与指数函数的单调性即可得出．‎ ‎【详解】a=20.3＞20=1，b=logπ3∈（0，1），c=log40.3＜log41=0，‎ 则a＞b＞c．‎ 故选：B．‎ ‎【点睛】本题考查了对数函数的单调性，考查了推理能力与计算能力，属于基础题．‎ ‎4.函数的零点所在的区间是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎∵函数，‎ ‎∴，‎ ‎∴函数数在定义域(0,+∞)上是单调增函数；‎ 又x=2时,，‎ x=e时,，‎ 因此函数的零点在(2,e)内。‎ 故选：C.‎ 点睛：本题主要考查了函数的零点与方程的关系;分段函数的应用等知识点. 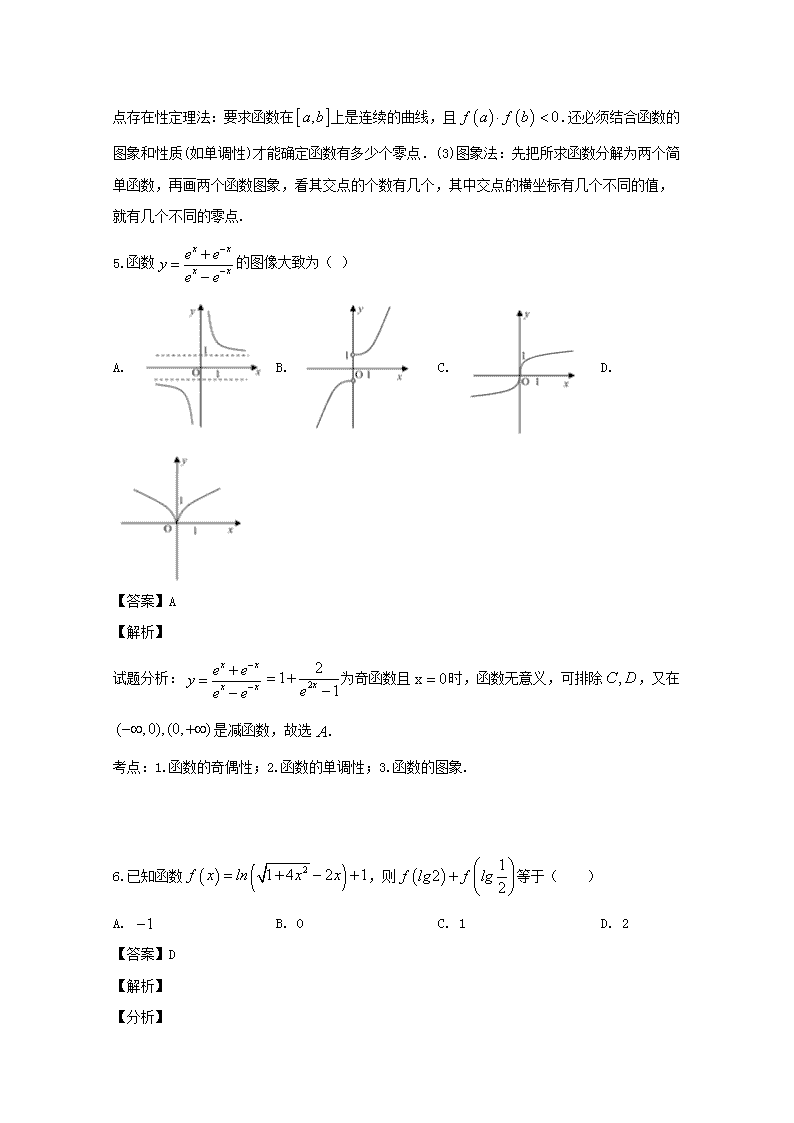函数零点个数的判断方法：(1)直接求零点：令 ‎，如果能求出解，则有几个解就有几个零点．(2)零点存在性定理法：要求函数在上是连续的曲线，且.还必须结合函数的图象和性质(如单调性)才能确定函数有多少个零点．(3)图象法：先把所求函数分解为两个简单函数，再画两个函数图象，看其交点的个数有几个，其中交点的横坐标有几个不同的值，就有几个不同的零点.‎ ‎5.函数的图像大致为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ 试题分析：为奇函数且时，函数无意义，可排除，又在是减函数，故选.‎ 考点：1.函数的奇偶性；2.函数的单调性；3.函数的图象.‎ ‎6.已知函数，则等于（ ）‎ A. B. 0 C. 1 D. 2‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据题意，由函数的解析式求出f（-x），进而可得f（-x）+f（x）=2，据此可得f（lg2）+f（lg）的值，即可得答案．‎ ‎【详解】根据题意，函数，则f（-x）=，‎ 则f（-x）+f（x）=ln1+2=2，‎ 则有f（lg2）+f（lg）=f（lg2）+f（-lg2）=2，‎ 故选：D．‎ ‎【点睛】本题考查函数的奇偶性的性质以及应用，涉及对数的计算，属于基础题．‎ ‎7.已知f(x)是定义在R上的奇函数，当x≥ 0时，f(x)＝x2－3x，则函数g(x)＝f(x)－x＋3的零点的集合为(　　)‎ A. {1,3} B. {－3，－1,1,3}‎ C. {2－，1,3} D. {－2－，1,3}‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 首先根据是定义在上的奇函数，求出函数在上的解析式，再求出 的解析式，根据函数零点就是方程的解，问题得以解决．‎ ‎【详解】∵是定义在上的奇函数，当x时，， 令，则 ， ‎ ‎ ，‎ ‎ 令， 当时，，解得 ‎， 当时，，解得 ‎ ‎∴函数的零点的集合为.‎ 故选：D．‎ ‎【点睛】本题考查函数的奇偶性及其应用，考查函数的零点，函数方程思想．属中档题.‎ ‎8.若函数在区间上是减函数，则实数的取值范围是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】‎ 试题分析：函数在区间上是减函数等价于在区间单调递减且，所以，解得，故选D.‎ 考点：1.对数函数的性质；2.复合函数的单调性.‎ ‎9.已知函数f(x)＝ex－1，g(x)＝－x2＋4x－3，若有f(a)＝g(b)，则b的取值范围为 (　　)．‎ A. [2－，2＋] B. (2－，2＋)‎ C. [1,3] D. (1,3)‎ ‎【答案】B ‎【解析】‎ 试题分析：由题可知f（x）＝ex－1>－1，g（x）＝－x2＋4x－3＝－（x－2）2＋1≤1，若有f（a）＝g（b），则g（b）∈（－1,1]．即－b2＋4b－3>－1，解得2－