新教材数学北师大版（2019）必修第二册课件：1-5-1 正弦函数的图象与性质再认识 课件（79张） 79页

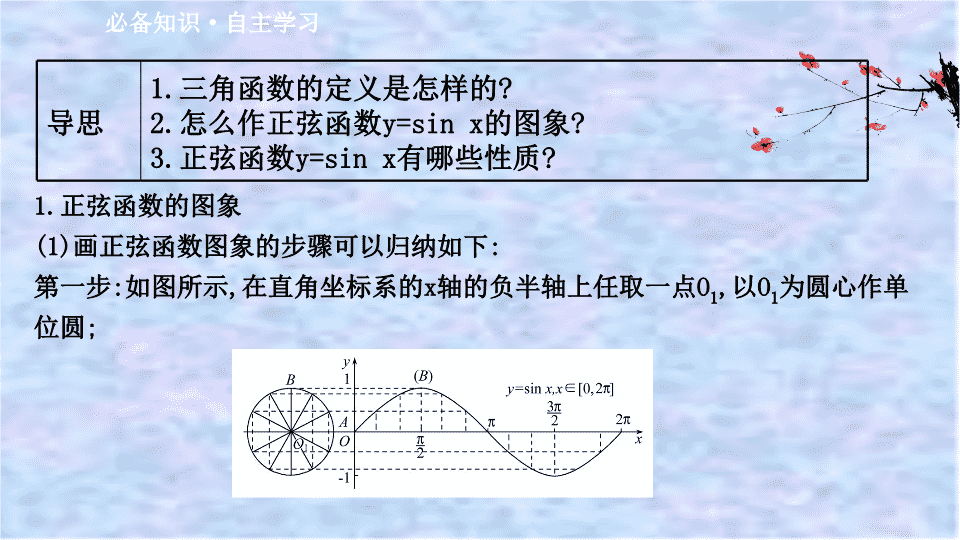
§5　正弦函数、余弦函数的图象与 性质再认识 5.1　正弦函数的图象与性质再认识 必备知识·自主学习 1.正弦函数的图象 (1)画正弦函数图象的步骤可以归纳如下: 第一步:如图所示,在直角坐标系的x轴的负半轴上任取一点O1,以O1为圆心作单 位圆; 导思 1.三角函数的定义是怎样的? 2.怎么作正弦函数y=sin x的图象? 3.正弦函数y=sin x有哪些性质? 第二步:从圆O1与x轴的交点A起把圆弧分成12等份; 第三步:过圆O1上各分点分别作x轴的垂线,得到对应于角0, , , ,…,2π 等分点的正弦值; 第四步:相应地,再把x轴上从0到2π这一段分成12等份; 第五步:再把角x所对应的正弦线向右平移,使它的起点与x轴上表示数x的点重 合; 第六步:最后用光滑曲线把这些正弦线的终点连接起来,就得到了正弦函数 y=sin x,x∈[0,2π]的图象. (2)五点法作正弦函数的图象,五个点为. (0,0), ,(π,0), ,(2π,0). 6  3  2  ( ,1)2  3( , 1)2   2.正弦函数的性质 (1)定义域:R. (2)周期性:最小正周期为2π. (3)单调性:单调增区间: (k∈Z), 单调减区间: (k∈Z). [2k ,2k ]2 2    － 3[2k ,2k ]2 2      (4)值域:[-1,1]. 当且仅当x=2kπ+ (k∈Z)时,正弦函数y=sin x取得最大值1; 当且仅当x=2kπ- (k∈Z)时,正弦函数y=sin x取得最小值-1. (5)奇偶性:正弦函数y=sin x在R上是奇函数. (6)对称性:对称轴x=kπ+ ,k∈Z,对称中心(kπ,0),k∈Z. 2  2  2  【思考】 (1)-2π是正弦函数的周期吗? 提示:是.2kπ(k∈Z,k≠0)都是它的周期. (2)正弦函数的对称轴之间的距离有什么特点?对称中心呢? 提示:对称轴之间的距离差了π的整数倍.对称中心之间也相差了π的整数倍. 【基础小测】 1.辨析记忆(对的打“√”,错的打“×”) (1)正弦函数在区间 上是递增的.(　　) (2)若存在一个常数T,使得对定义域内的每一个x,都有f(x+T)=f(x),则函数f(x) 为周期函数.(　　) (3)函数f(x)=sin x-1的一个对称中心为(π,-1).(　　) 2[ , ]6 3   提示:(1)×.正弦函数在区间 上先递增,再递减. (2)×.应为非零常数T. (3)√.因为正弦函数的一个对称中心为(π,0),函数f(x)=sin x-1即将正弦函 数向下平移一个单位,故一个对称中心为(π,-1). 2[ , ]6 3   2.函数y=sin x是(　　)　　　　　　　　　　　　　　　　　　 A.增函数 B.减函数 C.偶函数 D.周期函数 【解析】选D.由正弦曲线y=sin x的图象,可得函数y=sin x的增区间是 (k∈Z),减区间是 (k∈Z),函数是奇函数,且是 周期为2π的周期函数. [ 2k 2k ]2 2      ， 3[ 2k 2k ]2 2     ， 3.(教材二次开发:例题改编)下列关系式中正确的是(　　) A.sin 11°1;②y<1. (2)若直线y=a与y=1-2sin x有两个交点,求a的取值范围; (3)求函数y=1-2sin x的最大值,最小值及相应的自变量的值. 【思路导引】用五点法作图.再根据函数y=1-2sin x,x∈[-π,π]的简图解题. 【解析】按五个关键点列表 x -π 0 π sin x 0 -1 0 1 0 1-2sin x 1 3 1 -1 1 2  2  描点连线得: (1)由图象可知函数y=1-2sin x在y=1上方 的部分y>1,在y=1下方的部分y<1, 所以当x∈(-π,0)时,y>1,当x∈(0,π)时,y<1. (2)如图,当直线y=a与y=1-2sin x有两个交点时,1sin . 2  18  10  [ ,0]2  ( )18  ( )10  (2)因为cos =sin ,又 , 而正弦函数y=sin x在 上是减函数 所以sin >sin ,即sin >cos . 2.因为y=-2sin x-1, 所以函数y=-2sin x-1的递增区间就是函数y=sin x的递减区间.所以 +2kπ ≤x≤ +2kπ(k∈Z), 所以函数y=-2sin x-1的递增区间为 (k∈Z). 5 3 5( )2 3   7 5 3 2 4 2 3 2   ＜ ＜ ＋ ＜ 3[ , ]2 2   7 4 5( )2 3   7 4 5 3 2  3 2  3[ 2k , 2k ]2 2      【解题策略】 利用正弦函数单调性比较大小的步骤 (1)一定:利用诱导公式把角化到同一单调区间上. (2)二比较:利用函数的单调性比较大小. 【跟踪训练】 1.函数y=9-sin x的单调递增区间是(　　) A. (k∈Z) B. (k∈Z) C. (k∈Z) D. (k∈Z) 【解析】选B.y=9-sin x的单调递增区间与y=sin x的单调递减区间相同. [2k ,2k ]2 2      3[2k ,2k ]2 2      [2k ,2k ]    [2k ,2k ]    2.比较大小: (1)sin 250°与sin 260°;(2)sin 与sin . 【解析】(1)sin 250°=sin(180°+70°)=-sin 70°,sin 260°=sin(180°+ 80°)=-sin 80°, 因为0°<70°<80°<90°,且函数y=sin x,x∈ 是增函数,所以sin 70° -sin 80°,即sin 250°>sin 260°. 23( )5   17( )4   [0, ]2  (2)sin =-sin =-sin =-sin =-sin . sin =-sin =-sin . 因为0< < < ,且函数y=sin x,x∈ 是增函数,所以sin -sin , 即sin 0时,由题意 解得 [0, ]2  a b 1, 3a b 5,        a 2, b 1,     a b 5, 3a b 1,      － － a 2, b 7.    － 2.f(x)=sin(π+x)+sin2x-1=sin2x-sin x-1,令t=sin x,则y=t2-t-1= - ,t∈ . 因为-1≤t≤1,所以- ≤y≤1, 所以ymax=1,此时sin x=-1,x=- +2kπ,k∈Z; 所以ymin=- ,此时sin x= ,x= +2kπ,k∈Z或x= +2kπ,k∈Z. 21(t )2  5 4 [ 1,1] 5 4 2  5 4 1 2 6  5 6  【解题策略】 与正弦函数有关的函数的值域(或最值)的求法 (1)求形如y=asin x+b的函数的最值或值域时,可利用正弦函数的有界性 (-1≤sin x≤1)求解. (2)求形如y=asin2x+bsin x+c,a≠0,x∈R的函数的值域或最值时,可以通过换元, 令t=sin x,将原函数转化为关于t的二次函数,利用配方法求值域或最值.求解 过程中要注意正弦函数的有界性. 【跟踪训练】 1.求使下列函数取得最大值和最小值时的x值,并求出函数的最大值和最小值: (1)y=2sin x-1;(2)y=-sin2x+ sin x+ .2 3 4 【解析】(1)由-1≤sin x≤1知,当x= +2kπ,k∈Z时函数y=2sin x-1取得最大 值,ymax=1; 当x= π+2kπ,k∈Z时函数y=2sin x-1取得最小值,ymin=-3. (2)y=-sin2x+ sin x+ = ,因为-1≤sin x≤1,所以当 sin x= ,即x= +2kπ或x= +2kπ(k∈Z)时,函数取得最大值,ymax= ; 当sin x=-1,即x= +2kπ(k∈Z)时,函数取得最小值,ymin=- - . 3 2 2  2 3 4 22 5 (sinx )2 4－ － ＋ 2 2 4  3 4  5 4 3 2  1 4 2 2.设f(x)=asin x+b的最大值是1,最小值是-3,试确定g(x)=b2sin x+a2的最大值. 【解析】由题意,a≠0, 当a>0时, 所以 此时g(x)=sin x+4的最大值为5. 当a<0时, 所以 此时g(x)=sin x+4的最大值为5. 综上知g(x)的最大值为5. a b 1, a b 3,    ＋ ＝ － ＋ ＝－ a 2 b 1    ＝ ， ＝－ ， a b 3 a b 1    ＋ ＝－ ， － ＋ ＝ ， a 2 b 1,    ＝－ ， ＝－ 备选类型　正弦函数图象与性质的应用(直观想象、数学运算) 【典例】1.函数f(x)= -sin x在区间[0,2π]上的零点个数为(　　)　　　　　 　　　　　 　　　　　 A.1 B.2 C.3 D.4 2.求函数y= 的定义域、值域和零点. 【思路导引】1.转化为函数图象的交点个数判断. 2.按照相关的概念列式,结合不等式、方程求解. x1( )3 3 2sin x－ 【解析】1.选B.令f(x)= -sin x=0,即 =sin x,如图所示. 函数y= 与y=sin x在[0,2π]上有两个交点, 故函数f(x)= -sin x有两个零点. x1( )3 x1( )3 x1( )3 x1( )3 2.令 -2sin x≥0,即sinx≤ , 解得 +2kπ≤x≤ +2kπ,k∈Z, 所以函数的定义域为 ,k∈Z. 因为-1≤sin x≤ ,所以0≤ -2sin x≤ +2, 所以0≤ ≤ , 故函数的值域为 . 令y= =0, 解得x= +2kπ或x= π+2kπ,k∈Z. 3 3 2 2 3  7 3  2 7[ 2k , 2k ]3 3       3 2 3 3 3 2sin x－ 3 2 [0, 3 2] 3 2sin x－ 2 3  7 3 【解题策略】 关于正弦函数性质、图象的应用 (1)周期性的应用:正弦函数是周期函数,可以先研究其在一个周期内的性质,再 推广到定义域内. (2)奇偶性的应用:先确定函数的奇偶性,只研究函数在[0,+∞)上的性质,再利 用奇偶函数的性质推广到(-∞,0]上. (3)数形结合的应用:将问题转化为正弦函数与其他初等函数图象间的关系,利 用图象解决问题. 【跟踪训练】 1.(2020·福州高一检测)函数y= 的定义域为(　　)2sin( 2x) 1   5A.{x|2k x 2k ,k Z}6 6 5B.{x|k x k ,k Z}6 6 2C.{x|2k x 2k ,k Z}3 3 5D.{x|k x k ,k Z}12 12                                 【解析】选D.要使函数有意义,则2sin(π-2x)-1≥0, 即sin2x≥ ,则2kπ+ ≤2x≤2kπ+ ,k∈Z, 则kπ+ ≤x≤kπ+ ,k∈Z, 即函数的定义域为 . 1 2 6  5 6  12  5 12  5{x|k x k ,k Z}12 12         2.函数f(x)=sin x- 的零点个数是(　　) A.4 B.5 C.6 D.7 【解析】选D.令f(x)=sin x- =0,即sin x= , 令y1=sin x,y2= ,在同一坐标系内分别作出y1,y2的图象如图. 由图象可知图象有7个交点,即函数有7个零点. x 10 x 10 x 10 x 10 【补偿训练】 求方程sin x=lg x的解的个数. 【解析】建立平面直角坐标系xOy,先用五点法画出函数y=sin x,x∈[0,2π] 的图象,再向右连续平移2π个单位,得到y=sin x的图象. 描出点(1,0),(10,1),并用光滑曲线连接得到y=lg x的图象,如图所示. 由图象可知方程sin x=lg x的解有3个. 1.(教材二次开发:练习改编)函数y=2-sin x在______上单调递增,在区间 ________上单调递减.当x=______时,y取最大值______,当x=________时,y取最 小值________.  【解析】函数y=2-sin x的单调递增区间是函数y=sin x的单调递减区间即 (k∈Z), 同理可得单调递减区间是 (k∈Z), 当x=2kπ- ,k∈Z时,y取最大值3. 当x=2kπ+ ,k∈Z时,y取最小值1. 课堂检测·素养达标 3[2k ,2k ]2 2      [2k ,2k ]2 2      2  2  答案: (k∈Z) (k∈Z)　2kπ- ,k∈Z　3　 2kπ+ ,k∈Z　1 3[2k ,2k ]2 2      [2k ,2k ]2 2      2  2  2.已知a∈R,函数f(x)=sin x-|a|,x∈R为奇函数,则a等于________. 【解析】定义域x∈R,因为f(-x)=sin(-x)-|a|=-sin x-|a|,又f(x)=-f(-x), 所以sin x-|a|=sin x+|a|,所以|a|=0,即a=0. 答案:0 3.用五点法画出函数y=-2sin x在区间[0,2π]上的简图. 【解析】列表: x 0 π 2π sin x 0 1 0 -1 0 -2sin x 0 -2 0 2 0 2  3 2  描点、连线得y=-2sin x的图象如图. 七　正弦函数的图象与性质再认识 【基础通关——水平一】 (15分钟　30分) 1.以下对正弦函数y=sin x的图象描述不正确的是 (　　) A.在x∈[2kπ,2kπ+2π](k∈Z)时的图象形状相同,只是位置不同 B.介于直线y=1与直线y=-1之间 C.关于x轴对称 D.与y轴仅有一个交点 课时素养评价 【解析】选C.由正弦函数y=sin x在x∈[2kπ,2kπ+2π](k∈Z)时的图象可知 C项不正确. 2.不等式sin x≥ ,x∈(0,2π)的解集为 (　　)2 2 3A.[ ] B.[ ]6 2 4 4 3C.[ ] D.[ ]2 4 6 4         ， ， ， ， 【解析】选B.因为sin x≥ ,x∈(0,2π),结合y=sin x的图象知 ≤x≤ ,故不等式sin x≥ 的解集为 . 2 2 4  3 4  2 2 3[ , ]4 4   3.函数y=sin x,x∈ ,则y的范围是(　　) A.[-1,1]　 B. C. 　 D. 【解析】选C.当x= 时,y取最小值 ,当x= 时y取最大值1. 2[ , ]6 3   1 3[ , ]2 2 1[ ,1]2 3[ ,1]2 6  2 1 2 4.函数y= 的定义域为 (　　) A.[0,π]　 B.{第一或第二象限的角} C.{x|2kπ≤x≤(2k+1)π,k∈Z} D.(0,π) 【解析】选C.要使函数y= 有意义,则需sin x≥0,由y=sin x的图象 可得{x|2kπ≤x≤(2k+1)π,k∈Z}. sin x sin x 5.函数y=-2sin x+10取最小值时,自变量x的集合是________. 【解析】由题意知y=-2sin x+10取最小值,就是sin x取最大值,即x= +2kπ,k∈Z. 答案: 2  {x | x 2k k Z}2   ＝ ＋ ， 6.求函数y=(sin x-1)2+2的最大值和最小值,并说出取得最大值和最小值时相 应的x的值. 【解析】设t=sin x,则有y=(t-1)2+2, 且t∈[-1,1],在闭区间[-1,1]上, 当t=-1时,函数y=(t-1)2+2取得最大值(-1-1)2+2=6.由t=sin x=-1,得x=2kπ- (k∈Z), 即当x=2kπ- (k∈Z)时,函数y=(sin x-1)2+2取得最大值6.在闭区间[-1,1]上, 2  2  当t=1时, 函数y=(t-1)2+2取得最小值,最小值为2. 由t=sin x=1,得x=2kπ+ (k∈Z), 即当x=2kπ+ (k∈Z)时,函数y=(sin x-1)2+2取得最小值2. 2  2  【能力进阶——水平二】 (30分钟　60分) 一、单选题(每小题5分,共20分) 1.已知a= sin 59°,b=sin 15°+cos 15°,c=2 sin 31°·cos 31°, 则实数a,b,c的大小关系是(　　) A.a0,而图中显然小于零,因此排除选项B. 3.已知函数f(x)=2sin x,对任意的x∈R都有f(x1)≤f(x)≤f(x2),则|x1-x2|的 最小值为 (　　) A. B. C.π D.2π 【解析】选C.由不等式f(x1)≤f(x)≤f(x2)对任意x∈R恒成立,不难发现f(x1), f(x2)分别为f(x)的最小值和最大值,故|x1-x2|的最小值为函数f(x)=2sin x的 半个周期.因为f(x)=2sin x的周期为2π,所以|x1-x2|的最小值为π. 2  4  4.设函数y=sin x的定义域为[m,n],值域为 ,令t=n-m,则t的最大值与最 小值的和为 (　　) A.2π B. C.π D. 1[ ,1]2  3 2  2 3  【解析】选A.因为函数y=sin x的定义域为[m,n],值域为 ,结合正弦函数 y=sin x的图象与性质,不妨取m=- ,n= ,此时n-m取得最大值为 ,取 m=- ,n= ,n-m取得最小值为 ,则t的最大值与最小值的和为2π. 1[ ,1]2  6  7 6  4 3  6  2  2 3  二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错 的得0分) 5.已知函数f(x)= ·cos x,则下列说法正确的是 (　　) A.f(x)的最小正周期为π B.f(x)的图象关于 中心对称 C.f(x)在区间 上单调递增 D.f(x)的值域为[-1,1] sin x cos x ( ,0)2  ( , )2   【解析】选BC.因为函数f(x)= ·cos x= 画出函数f(x)的图象,如图所示: f(x)的最小正周期是2π,根据f(x)的图象,f(x)的图象关于 中心对称,f(x) 在区间 上单调递增,f(x)的值域为(-1,1). sin x cos x sin x x [k k ) k Z2 sin x x (k k ] k Z2               ， ， ， ， ， ， ， ， ( ,0)2  ( , )2   6.函数f(x)=sin x+2|sin x|,x∈[0,2π]的图象与直线y=k的交点个数可能是 (　　) A.0　　 B.1　　 C.2　　 D.3 【解析】选ABCD.f(x)=sin x+2|sin x|= 在同一坐标系内分 别作出函数y=f(x)与y=k的图象,如图所示, 当k>3或k<0时,两图象无交点;当k=3时,两图象有1个交点;当10得sin x>- , 解得- +2kπ0时, 由题意,得 解得 所以f(x)=-2sin x,此时f(x)的最大值为2,最小值为-2. 1 2 3 2 3a b ,2 1a b ,2        1a ,2 b 1.     ②当b<0时,由题意,得 解得 所以f(x)=2sin x,此时f(x)的最大值为2,最小值为-2. 3a b ,2 1a b ,2       1a ,2 b 1      ， 【创新迁移】 1.对于函数f(x)=asin(π-x)+bx+c(其中a,b∈R,c∈Z),选取a,b,c的一组值计 算f(1)和f(-1),所得出的正确结果一定不可能是(　　) A.4和6 B.3和1 C.2和4 D.1和2 【解析】选D.因为sin(π-x)=sin x, 所以f(x)=asin x+bx+c, 则f(1)=asin 1+b+c,f(-1)=asin(-1)+b×(-1)+c=-asin 1-b+c, 所以f(-1)=-f(1)+2c.① 把f(1)=4,f(-1)=6代入①式,得c=5∈Z,故排除A; 把f(1)=3,f(-1)=1代入①式,得c=2∈Z,故排除B; 把f(1)=2,f(-1)=4代入①式,得c=3∈Z,故排除C; 把f(1)=1,f(-1)=2代入①式,得c= ∉ Z.3 2 2.已知函数f(x)=-sin2x+sin x+a,若1≤f(x)≤ 对一切x∈R恒成立,求实数a 的取值范围. 17 4 【解析】令t=sin x,t∈[-1,1],则原函数可化为g(t)=-t2+t+a=- +a+ . 当t= 时,g(t)max=a+ ,即f(x)max=a+ ; 当t=-1时,g(t)min=a-2,即f(x)min=a-2. 故对于一切x∈R,函数f(x)的值域为 . 所以 解得3≤a≤4. 21(t )2  1 4 1 2 1 4 1 4 1[a 2 a ]4－ ， ＋ 1 17a 4 4 a 2 1     ＋ ， － ，