西藏自治区山南市第三高级中学2020届高三第三次模拟考试前自查自测调研考试数学（文）一试卷 15页

文 科 数 学（一）‎ 注意事项：‎ ‎1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。‎ ‎2．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。‎ ‎3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。‎ ‎4．考试结束后，请将本试题卷和答题卡一并上交。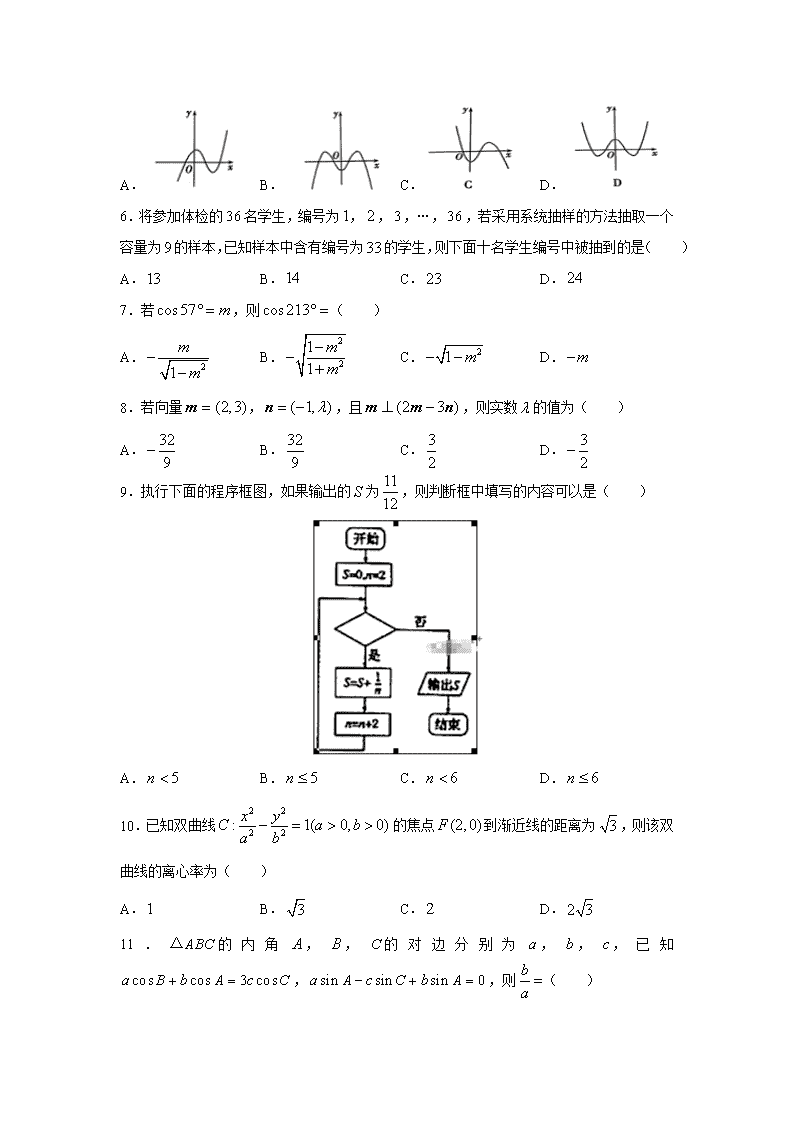‎ 第Ⅰ卷 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，‎ 只有一项是符合题目要求的．‎ ‎1．设，则（ ）‎ A． B． C． D．‎ ‎2．设集合，，则（ ）‎ A． B． C． D．‎ ‎3．已知，，，则下列关系正确的是（ ）‎ A． B．‎ C． D．‎ ‎4．定义：，当五位数满足，且时，称这个五位数为“凸数”．由，，，，组成的没有重复数字的五位数共个，从中任意抽取一个，则其恰好为“凸数”的概率为（ ）‎ A． B． C． D．‎ ‎5．函数的图象大致是（ ）‎ A． B． C． D．‎ ‎6．将参加体检的名学生，编号为，，，…，，若采用系统抽样的方法抽取一个容量为的样本，已知样本中含有编号为的学生，则下面十名学生编号中被抽到的是（ ）‎ A． B． C． D．‎ ‎7．若，则（ ）‎ A． B． C． D．‎ ‎8．若向量，，且，则实数的值为（ ）‎ A． B． C． D．‎ ‎9．执行下面的程序框图，如果输出的为，则判断框中填写的内容可以是（ ）‎ A． B． C． D．‎ ‎10．已知双曲线的焦点到渐近线的距离为，则该双曲线的离心率为（ ）‎ A． B． C． D．‎ ‎11．的内角，，的对边分别为，，，已知，，则（ ）‎ A． B． C． D．‎ ‎12．抛物线的焦点是双曲线的一个焦点，过且倾斜角为的直线交于、，则（ ）‎ A． B． C． D．‎ 第Ⅱ卷 二、填空题：本大题共4小题，每小题5分，共20分．‎ ‎13．已知曲线在点处的切线方程为，则实数的值为 ．‎ ‎14．已知正项等比数列的前项和为，若，，则 ．‎ ‎15．函数的最大值为 ．‎ ‎16．已知正方体的棱长为，为棱的中点，点在正方形内运动，且直线平面，则动点的轨迹长度为 ．‎ 三、解答题：本大题共6个大题，共70分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（12分）某高中为了了解高三学生每天自主参加体育锻炼的情况，随机抽取了名学生进行调查，其中女生有名．下面是根据调查结果绘制的学生自主参加体育锻炼时间的频率分布直方图：‎ 将每天自主参加体育锻炼时间不低于分钟的学生称为体育健康类学生，已知体育健康 类学生中有名女生．‎ ‎（1）根据已知条件完成下面列联表，并据此资料你是否有的把握认为达到体育健康类学生与性别有关？‎ 非体育健康类学生 体育健康类学生 合计 男生 女生 合计 ‎（2）将每天自主参加体育锻炼时间不低于分钟的学生称为体育健康类学生，已知体育健康类学生中有名女生，若从体育健康类学生中任意选取人，求至少有名女生的概率．‎ 附：‎ ‎18．（12分）已知等差数列的首项为，公差为，前项的和为，且，．‎ ‎（1）求数列的通项公式；‎ ‎（2）设数列的前项和为，求．‎ ‎19．（12分）如图1，在直角梯形中，，，且，现以为一边向梯形外作正方形，然后沿边将正方形翻折，使平面与平面垂直，如图2．‎ ‎（1）求证：平面；‎ ‎（2）求点到平面的距离．‎ ‎20．（12分）已知函数．‎ ‎（1）若在上只有一个零点，求的取值范围；‎ ‎（2）设为的极小值点，证明：．‎ ‎21．（12分）已知动点到点的距离比到直线的距离小，设点的轨迹为曲线．‎ ‎（1）求曲线的方程；‎ ‎（2）过曲线上一点作两条直线，与曲线分别交于不同的两点，，若直线，的斜率分别为，，且，证明：直线过定点．‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．‎ ‎22．（10分）【选修4-4：坐标系与参数方程】‎ 已知斜率为的直线经过点．‎ ‎（1）写出直线的参数方程；‎ ‎（2）设直线与圆相交于，两点，求的值．‎ ‎23．（10分）【选修4-5：不等式选讲】‎ 已知．‎ ‎（1）解不等式；‎ ‎（2）若不等式（，）对任意的都成立，证明：‎ 文 科 数 学（一）答 案 第Ⅰ卷 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，‎ 只有一项是符合题目要求的．‎ ‎1．【答案】B ‎【解析】．‎ ‎2．【答案】A ‎【解析】，．‎ ‎3．【答案】A ‎【解析】∵，，，‎ 因为，即，∴．‎ ‎4．【答案】D ‎【解析】由题意，由，，，，组成的没有重复数字的五位数恰好为“凸数”的有：‎ ‎，，，，，，共个基本事件，‎ 所以恰好为“凸数”的概率为．‎ ‎5．【答案】D ‎【解析】由为偶函数可排除A，C；‎ 当时，图象高于图象，即，排除B，故选D．‎ ‎6．【答案】A ‎【解析】从名学生中抽取名，抽样间隔为，‎ 所以名学生的编号分别为，，，，，，，，．‎ ‎7．【答案】C ‎【解析】．‎ ‎8．【答案】B ‎【解析】由题意得，，‎ ‎∵，∴，即，解得．‎ ‎9．【答案】D ‎【解析】运行程序，，判断是，，判断是，，判断是，，判断否，输出，故答案为D．‎ ‎10．【答案】C ‎【解析】由题意知双曲线的焦点到渐近线的距离为，，‎ 所以，该双曲线的离心率为．‎ ‎11．【答案】A ‎【解析】在中，由正弦定理及，‎ 得，∴，‎ 又，∴，‎ 由正弦定理及，得，‎ ‎∴由余弦定理得，即，∴．‎ ‎12．【答案】D ‎【解析】双曲线，∴焦点，∴，，∴，‎ 直线，由，得，，‎ ‎．‎ 第Ⅱ卷 二、填空题：本大题共4小题，每小题5分，共20分．‎ ‎13．【答案】‎ ‎【解析】，，∴．‎ ‎14．【答案】‎ ‎【解析】因为，，所以，，‎ 两式相除可得，，，‎ 由题设知舍，故，，．‎ ‎15．【答案】‎ ‎【解析】，‎ ‎∵，∴的最大值为．‎ ‎16．【答案】‎ ‎【解析】设平面与直线交于点，连接，则为的中点．‎ 分别取、的中点、，连接、、，‎ 则∵，，，平面，，平面，‎ ‎∴平面．同理可得平面，‎ ‎∵、是平面内相交直线，∴平面平面，‎ 所以平面，‎ ‎∴的轨迹被正方形截得的线段是线段，‎ ‎∴的轨迹被正方形截得的线段长．‎ 三、解答题：本大题共6个大题，共70分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．【答案】（1）列联表见解析，没有的把握认为；（2）．‎ ‎【解析】（1）右频率分布直方图可知，在抽取的100人中，体育健康A类学生有25人，‎ 从而列联表如下：‎ 非体育健康类学生 体育健康类学生 合计 男生 女生 合计 由列联表中数据代入公式计算，得：‎ ‎，‎ 所以没有的把握认为达到体育健康类学生与性别有关．‎ ‎（2）由频率分布直方图可知，体育健康类学生为人，记表示男生，表示女生，从而一切可能结果所组成的基本事件空间为．‎ 由个基本事件组成，而且这些事件的出现是等可能的．‎ 用表示“任选人中至少有名是女生”这一事件，‎ 则共计7种，‎ ‎∴．‎ ‎18．【答案】（1）；（2）．‎ ‎【解析】（1）由题意可得，解得，‎ ‎∴．‎ ‎（2）∴，‎ ‎∴．‎ ‎19．【答案】（1）证明见解析；（2）．‎ ‎【解析】（1）在正方形中，，‎ 又因为平面平面，且平面平面，‎ 所以平面，可得，‎ 在直角梯形中，，，可得，‎ 在中，，，所以，‎ 所以，，所以平面．‎ ‎（2）因为平面，所以平面平面，‎ 过点作的垂线交于点，则平面，‎ 所以点到平面的距离等于线段的长度．‎ 在直角三角形中，，‎ 所以，所以点到平面的距离等于．‎ ‎20．【答案】（1）；（2）证明见解析．‎ ‎【解析】（1）因为在上只有一个零点，所以方程在上只有一个解，‎ 设函数，则，‎ 当时，；当时，，‎ 所以，‎ 又，，‎ 故的取值范围为．‎ ‎（2）证明：，当时，恒成立，无极值，故，‎ 令，得，‎ 当时，；当时，，‎ 故的极小值为，‎ 故要证，只需证：，‎ 设函数，，‎ 当时，；当时，，‎ 故，而，‎ 于是，从而．‎ ‎21．【答案】（1）；（2）证明见解析．‎ ‎【解析】（1）由题意可知，动点到点的距离与到直线的距离相等，‎ 所以点的轨迹是以为焦点，直线为准线的抛物线，‎ 所以曲线的方程为．‎ ‎（2）易知，设点，，直线的方程为，‎ 联立，得，所以，所以，‎ 因为，即，‎ 所以，所以，‎ 所以或，‎ 当时，直线的方程为过定点与重合，舍去；‎ 当时，直线的方程为过定点，‎ 所以直线过定点．‎ ‎22．【答案】（1）；（2）．‎ ‎【解析】（1）直线的参数方程为，‎ 即．‎ ‎（2）将代入，化简整理得，‎ 因为，，‎ 所以．‎ ‎23．【答案】（1）；（2）证明见解析．‎ ‎【解析】（1），即．‎ ‎①当时，，得；‎ ‎②当时，，得，不成立；‎ ‎③当时，，得，‎ 综上，所求的的取值范围是．‎ ‎（2）因为，所以．‎ 因为，时，，所以，得，‎ 所以，当且仅当时等号成立