【数学】2019届一轮复习人教A版三视图与直观图转化失误学案 19页

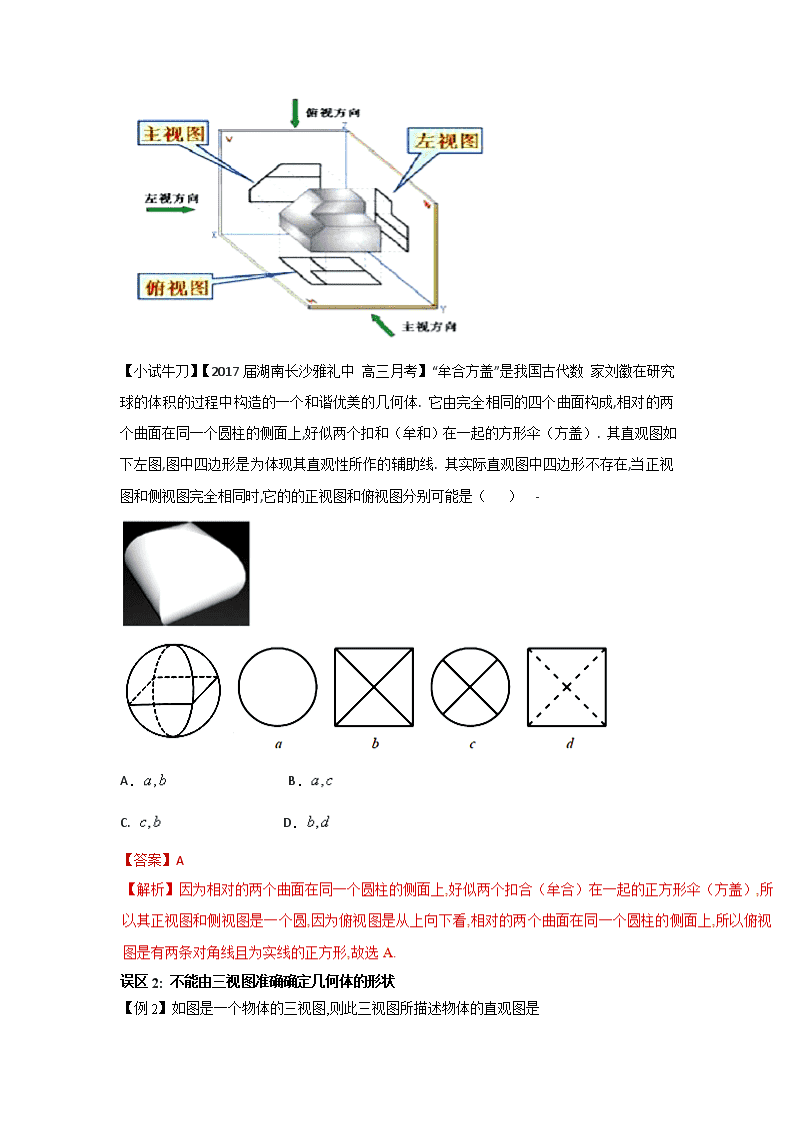
‎ ‎ ‎ 专题七 立体几何 误区一：三视图与直观图转化失误 一、易错提醒 由三视图确定几何体的形状或根据三视图确定几何体的其表面积或体积是高考命题的重点,这类问题多为客观题,求解过程中易出现的问题主要是三视图与直观图的转化不当导致错误.解决此类问题的关键是准确把握几何体的结构特征与三视图、直观图的画法法则.‎ 二、典例精析 误区1:不能准确判断三视图的形状 ‎【例1】如图,已知三棱锥的底面是直角三角形,直角边边长分别为3和4,过直角顶点的侧棱长为4,且 垂直于底面,该三棱锥的主视图是 (　　)‎ ‎【分析】首先根据空间直角坐标系明确几何体的摆放角度,然后根据主视图的定义,判断每个点在面xOy内的射影个,从而确定该几何体的主视图的形状. : , , ,X,X,K]‎ ‎【解析】显然由空间直角坐标系可知,该几何体在xoy面内的点保持不动,在y轴上的点在xoy面内的射影为坐标原点,所以该几何体的主视图就是其在面xoy面的表面图形,即主视图应为高为4,底面边长为3的直角三角形．故选B.‎ ‎【误区警示】该题易出现的问题是误以为y轴上的点在xoy面的射影落在x轴的正半轴上而误选D,判断几何体的三视图应注意以下结构方面：‎ ‎（1）明确几何体的放置位置和角度,注意投影线和投影面；‎ ‎（2）准确把握几何体的结构特征,特别是几何体中的线面垂直关系等；‎ ‎（3）注意实线和虚线的区别.‎ ‎【小试牛刀】【2017届湖南长沙雅礼中 高三月考】“牟合方盖”是我国古代数 家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体. 它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣和（牟和）在一起的方形伞（方盖）. 其直观图如下左图,图中四边形是为体现其直观性所作的辅助线. 其实际直观图中四边形不存在,当正视图和侧视图完全相同时,它的的正视图和俯视图分别可能是（ ） - ‎ A． B． ‎ C. D．‎ ‎【答案】A 误区2: 不能由三视图准确确定几何体的形状 ‎【例2】如图是一个物体的三视图,则此三视图所描述物体的直观图是 (　　)‎ ‎【分析】首先根据俯视图确定几何体的底面——圆,然后根据主视图和侧视图确定几何体的侧面,总而确定该几何体的直观图.‎ ‎【解析】直接根据选项判断,由俯视图可知是B和D中的一个,由主视图和左视图可知B错．‎ ‎【误区警示】该题易出现的问题是由主视图和侧视图下方部分误判断该几何体的下方为正方体导致错选A.由三视图确定几何体的直观图的关键是熟记简单几何体的三视图,这是解题的基础,确定几何体直观图一般按照从下到上、先实后虚的顺序,即先根据俯视图确定几何体底面,然后根据主视图和侧视图确定几何体的侧面或顶点,最后注意实线和虚线对应的图形的处理.‎ ‎【小试牛刀】【2017届湖南长沙一中高三月考】如图, 格纸上小正方形的边长为1,粗实线及粗虚线画出的某多面体的三视图,则该多面体外接球的表面积为（ ）[ : K]‎ A. B. ‎ C. D.‎ ‎【答案】D 误区3 数据不能准确转化 ‎【例3】已知正三棱锥V—ABC的主视图、左视图和俯视图如图所示．‎ ‎(1)画出该三棱锥的直观图；‎ ‎(2)求出左视图的面积．‎ ‎【分析】首先根据三视图的形状确定几何体的形状；然后利用三视图中的数据确定几何体的数字特征,进而确定左视图中的相应数据,求其面积.‎ ‎【解析】(1)如图所示．‎ ‎(2)根据三视图间的关系可得BC＝2,‎ ‎∴左视图中VA＝＝2,‎ ‎∴S△VBC＝×2×2＝6.‎ ‎【误区警示】该题中易出现的问题是左视图中的底边BC的长度求错.三视图中的数字特征转化为直观图中的数字特征时应注意正确利用三视图的作图法则：主视图与俯视图等长；主视图与侧视图等高；侧视图与俯视图等宽.‎ ‎【小试牛刀】【2017届甘肃高台县一中高三上 期检测五】某三棱锥的三视图如图所示,该三棱锥的表面积是（ ）[ : ]‎ A． B． ‎ C． D．‎ ‎【答案】D ‎【解析】画出直观图如下图所示,.‎ ‎【例4】一个空间几何体的三视图,如图所示,则这个空间几何体的表面积是________．‎ ‎【分析】由三视图还原成直观图或几何体,要注意几何体的不同放置；结合三视图的规则综合考虑,正确得到原几何体．‎ ‎【误区警示】该题易出现的问题是不能把三视图反映出的空间几何体的形状、大小准确的还原出来．在由三视图还原为空间几何体的实际形状时,要从三个视图综合考虑,根据三视图的规则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线在三视图中为虚线．在还原空间几何体实际形状时,一般是以主视图和俯视图为主,结合左视图进行综合考虑．‎ ‎【小试牛刀】一个几何体的三视图及其相关数据如图所示,求这个几何体的表面积．‎ ‎【解析】这个几何体是一个圆台被轴截面割出来的一半．‎ 根据图中数据可知圆台的上底面半径为1,下底面半径为2,高为,母线长为2,几何体的表面积是两个半圆的面积、圆台侧面积的一半和轴截面的面积之和,故这个几何体的表面积为S＝π×12＋π×22＋π×(1＋2)×2＋×(2＋4)×＝＋3.‎ 三、迁移运用 ‎1．【河南省2018届高三4月普通高中毕业班高考适应性考试】已知四棱锥的三视图如图所示，则四棱锥外接球的表面积是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】由三视图得，几何体是一个四棱锥A-BCDE,底面ABCD是矩形，侧面ABE⊥底面BCDE.‎ 如图所示，矩形ABCD的中心为M,球心为O,F为BE中点，OG⊥AF.设OM=x,‎ 由题得在直角△OME中，，又MF=OG=1,AF=,‎ ‎，解（1）（2）得故选B.‎ ‎2．【湖南省郴州市2018届高三第二次教 质量检测】某几何体的三视图如图所示,则该几何体的体积为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】由三视图可知，该几何体是一个组合体，它的组成是一个圆柱截去四分之一，再补上以直角边长为的等腰三角形为底面，圆柱上底面圆心为顶点的三棱锥，故体积为，故选C.‎ ‎3．【湖北省武汉市2018届高中毕业生二月调研】某四棱锥的三视图如图所示，其中正视图是斜边为等腰直角三角形，侧视图和俯视图均为两个边长为1的正方形，则该四棱锥的高为（ ）‎ A. B. 1 C. D. ‎ ‎【答案】A ‎【解析】几何体是是如图放置的四棱锥，是正方体中切除一个三棱柱，再切除一个三棱锥所得到的几何体，该正方体的棱长为1，高为到平面的距离，此距离为，故选A.‎ ‎4．【河南省南阳市2018届高三上 期期末】如图， 格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的外接球的表面积（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ 由三视图可知，该几何体为如图所示的四棱锥，图中正方体的棱长为 ， 该多面体如图所示，外接球的半径为为，外接圆的半径，由 可得 ，，故该多面体的外接球的表面积，故选C.‎ ‎5．【山东省济南市2018届高三上 期期末 ‎】某简单凸多面体的三视图如图所示，其中俯视图和左视图都是直角三角形，主视图是直角梯形，则其所有表面（含底面和侧面）中直角三角形的个数为（ ）‎ A. 1 B. 2 C. 3 D. 4‎ ‎【答案】A ‎【解析】‎ 由三视图可知，该凸多面体是如图所示的三棱锥 ，由图可知，三棱锥的三个面中，只有 是直角三角形，即直角三角形的个数为 ，故选A.‎ ‎6．【吉林省梅河口市第五中 2018届高三上 期第四次月考】如图是某几何体的三视图，则该几何体的体积为( )‎ A. 6 B. 9 C. 12 D. 18‎ ‎【答案】B ‎【解析】‎ 由已知中的三视图可得：该几何体是两个三棱柱形成的组合体，‎ 下部的三棱柱,底面面积为： ，高为1，体积为：6；‎ 上部的三棱柱,底面面积为： ×2×3=3，高为1，体积为：3；‎ 故组合体的体积V=6+3=9，‎ 故选：B.‎ ‎7．【2017届甘肃天水一中高三12月月考】正方体中为棱的中点（如图）,用过点,,的平面截去该正方体的上半部分,则剩余几何体的左视图为（ ）‎ ‎【答案】C ‎【解析】由已知可得剩余几何体的左视图应是选项C.‎ ‎8．【2017届云南曲靖一中高三上 期月考】一个几何体的三视图如图所示,那么该几何体的体积为（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】,故选A.‎ ‎9．【2017届河北武邑中 高三周考】已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一直角边为2的直角三角形,则该三棱锥的正视图可能为（ ）‎ ‎ ‎ ‎【答案】C[ : , , ,X,X,K]‎ ‎【解析】由俯视图可知三棱锥的底面是个边长为的正三角形,由侧视图可知三棱锥的一条侧棱垂直于底面,且其长度为,故其主视图为直角边长为的等腰直角三角形,且中间有一虚线,故选C．‎ ‎10．【2017届江西吉安一中高三上 期段考二】已知某几何体的三视图如图所示,则该几何体的各侧面中,面积最小值为（ ）‎ A． B． ‎ C. D．‎ ‎【答案】D ‎【解析】直观图如下图所示,由直观图可知,三角形的面积的面积最小,为.‎ ‎11．【2017届湖南长沙一中高三月考五】某几何体的三视图如图所示,则该几何体的体积为（ ）‎ A. B. ‎ C. D.‎ ‎【答案】C ‎12．【2017届湖南长沙雅礼中 高三月考】一个三棱锥的正视图和俯视图如下图所示,则该三棱锥的侧视图可能为（ ）‎ ‎【答案】D ‎【解析】根据几何体三视图的规则““长对正、宽相等、高平齐”的原则”,则该三棱锥的侧视图可能为选项D,故选D.‎ ‎13．【2017届河南南阳一中高三上 期月考四】将正三棱柱截去三个角如图1所示,、、分别是三边的中点,得到几何体如图2,则该几何体按图2所示方向的侧视图为（ ）‎ ‎【答案】A ‎【解析】由图和图可知,图的侧视图应是一个直角梯形,其上底是的边上的高,下底为的边上的高,直角腰为的边上的高,故侧视图应为A.‎ ‎14．【2017届河南南阳一中高三上 期月考四】某椎体的三视图如图所示,则该棱锥的最长棱的棱长为（ ）‎ A． B． C． D．‎ ‎【答案】C ‎15．【2017届广西柳州市高三10月模拟】如图,在一个正方体内放入两个半径不相等的球、,这两个球相外切,且球与正方体共顶点的三个面相切,球与正方体共顶点的三个面相切,则两球在正方体的面上的正投影是（ ）‎ ‎【答案】B ‎【解析】由三视图得球与正方体左面切点的投影在棱上,球与正方体上面切点的投影在棱上,球与正方体下面切点的投影在棱上,与正方体右面切点的投影在棱上,由于,所以两个圆有交点,有重叠,故选B ‎16．【2017届重庆巴蜀中 高三12月月考】如图所示,在三棱柱中,平面,,,,若规定主（正）视方向垂直平面,则此三棱柱的侧（左）视图的面积为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】由题设可知,且边上的高,侧视图是以边上的高为宽,长为棱长的矩形.故其面积为,应选A.‎ ‎17．【2017届湖南郴州市高三第二次质监】某几何体的三视图如图所示,则该几何体的体积为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】由三视图可知,该几何体为如下图所示的多面体,它是由三棱柱截去三棱锥后所剩的几何体,所以其体积,故选D.‎ ‎18．【2017届重庆市一中高三上 期期中】已知某棱锥的三视图如图所示,则该棱锥的表面积为（ ）‎ A. B. C. D.‎ ‎【答案】D