黑龙江省哈尔滨市第三中学校2019-2020学年高二上学期期末考试数学（文）试卷 7页

数学试题 文 考试说明：（1）本试卷分第I卷（选择题）和第II卷（非选择题）两部分，满分150分．‎ 考试时间为120分钟；‎ ‎ （2）第I卷，第II卷试题答案均答在答题卡上，交卷时只交答题卡．‎ 第I卷 （选择题, 共60分）‎ 一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的．‎ 1. 已知圆的方程为，则圆心坐标为 A． B． C． D． ‎ 2. 若，且为第四象限角，则的值为 A． B． C． D．‎ 3. 四张卡片上分别写有数字，若从这四张卡片中随机抽取两张，则抽取的两张卡片上的数字之和为奇数的概率是 ‎ A． B． C． D． ‎ 4. 已知椭圆E：与双曲线C：（）有相同的焦点，则双曲线C的渐近线方程为 A． B． C． D． ‎ 5. 在区间上随机取一个数，使直线与圆相交的概率为 A． B． C． D．‎ 1. 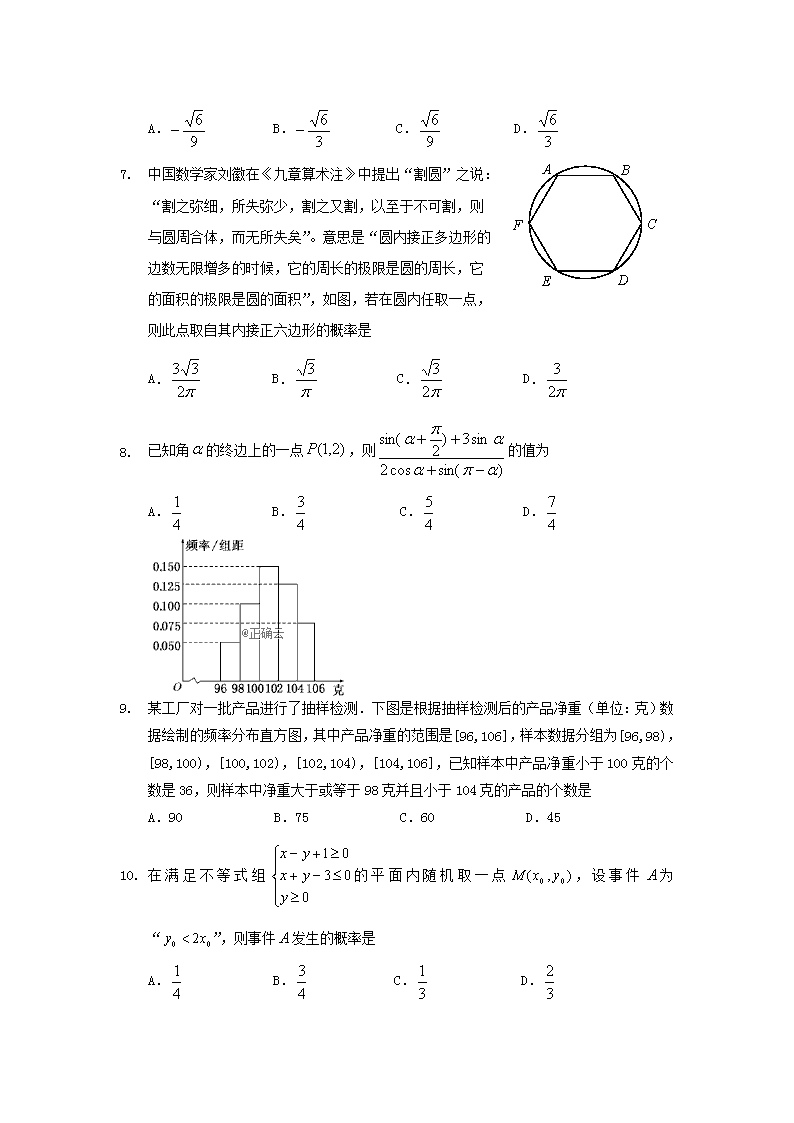已知均为锐角，，‎ A． B． C． D．‎ A B C D F E 2. 中国数学家刘徽在《九章算术注》中提出“割圆”之说：‎ ‎“割之弥细，所失弥少，割之又割，以至于不可割，则 与圆周合体，而无所失矣”。意思是“圆内接正多边形的 边数无限增多的时候，它的周长的极限是圆的周长，它 的面积的极限是圆的面积”，如图，若在圆内任取一点，‎ 则此点取自其内接正六边形的概率是 A． B． C． D． ‎ 3. 已知角的终边上的一点，则的值为 A． B． C． D． ‎ 4. 某工厂对一批产品进行了抽样检测．下图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96,106]，样本数据分组为[96,98)，[98,100)，[100,102)，[102,104)，[104,106]，已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是 ‎ A．90 B．75 C．60 D．45‎ 5. 在满足不等式组的平面内随机取一点，设事件为“”，则事件发生的概率是 A． B． C． D．‎ 1. 已知函数，满足，将函数的图象向右平移个单位得到函数的图象，若的图象关于直线对称，则的取值可以为 A．1 B．2 C．3 D．4‎ 2. 已知圆（圆心为点）与抛物线交于两点，若此抛物线的焦点为，且两点都在以为直径的圆上，则 A． B． C． D． ‎ 第Ⅱ卷 （非选择题, 共90分）‎ 二、填空题：本大题共4小题，每小题5分，共20分．将答案填在答题卡相应的位置上．‎ 3. 已知一个扇形的圆心角为3弧度，半径为4，则这个扇形的面积等于 ．‎ 4. 在平面直角坐标系中，曲线的参数方程为（为参数），直线的方程为，则曲线上的点到直线的距离的最大值为 ．‎ 5. 现采用随机模拟的方法估计某运动员射击4次，至少击中3次的概率：先由计算器给出0到9之间取整数值的随机数，指定0，1表示没有击中目标，2，3，4，5，6，7， 8，9表示击中目标，以4个随机数为一组，代表射击4次的结果，经随机模拟产生了 20组随机数：‎ ‎ 7527 0293 7140 9857 0347 4373 8636 6947 1417 4698 ‎ ‎ 0371 6233 2616 8045 6011 3661 9597 7424 7610 4281‎ 根据以上数据估计该射击运动员射击4次至少击中3次的概率为 ．‎ 6. 已知双曲线的左、右焦点分别为，是双曲线右支上的一点，射线平分交轴于点，过原点的直线平行于直线交于点，若，则双曲线的离心率为 ．‎ 三、 解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．‎ 1. ‎（本题10分）‎ 在平面直角坐标系中，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，已知直线（为参数）与抛物线交于两点，设点.‎ ‎（Ⅰ）求直线的普通方程和极坐标方程；‎ ‎（Ⅱ）求和.‎ 2. ‎（本题12分）‎ 设甲、乙、丙三个羽毛球协会的运动员人数分别为18，9，18，先采用分层抽样的方法从这三个协会中抽取5名运动员参加比赛.‎ ‎（Ⅰ）求应从这三个协会中分别抽取的运动员人数；‎ ‎（Ⅱ）将抽取的5名运动员进行编号，编号分别为，从这5名运动员中随机抽取2名参加双打比赛. 设“编号为的两名运动员至少有一人被抽到” 为事件A，求事件A发生的概率.‎ 3. ‎（本题12分）‎ 如图所示，“8”是在极坐标系中分别以和为圆心，外切于点的两个圆．过作两条夹角为的射线分别交圆于两点，交圆于两点．‎ ‎（Ⅰ）求圆和圆的极坐标方程；‎ ‎（Ⅱ）求面积的最大值．‎ 1. ‎（本题12分）‎ 某校为了诊断高三学生在市“一模”考试中文科数学备考的状况，随机抽取了50名学生的市“一模”数学成绩进行分析，将这些成绩分为九组，第一组[60，70)，第二组[70，80)，……，第九组[140，150]，并绘制了如图所示的频率分布直方图．‎ ‎（Ⅰ）试求出的值并估计该校文科数学成绩的众数和中位数；‎ ‎（Ⅱ）现从成绩在[120，150]的同学中随机抽取2人进行谈话，那么抽取的2人中恰好有一人的成绩在[130,140)中的概率是多少？‎ 2. ‎（本题12分）‎ 已知函数.‎ ‎（Ⅰ）求函数的最小正周期并用五点作图法画出函数在区间上的图象；‎ ‎（Ⅱ）若将函数的图象向右平移个单位长度，得到函数的图象，求函数的解析式，并求当时，函数的最小值及此时的值.‎ 1. ‎（本题12分）‎ 已知椭圆 的左、右焦点分别为，离心率为，过椭圆焦点且与长轴垂直的直线被椭圆截得的弦长为．‎ ‎（Ⅰ）求椭圆的标准方程；‎ ‎（Ⅱ）过椭圆左顶点A的直线与椭圆的另一个交点为M，与y轴交点为P，若点，且，求直线的方程.‎ 数学(文科)试题答案 一、选择题：本大题共12小题，每小题5分，共60分.‎ ADCBC AADAB BC 二、填空题：本大题共4小题，每小题5分，共20分． ‎ ‎13‎ ‎14‎ ‎15‎ ‎16‎ ‎24‎ 三、解答题： ‎ ‎17. （1），； ‎ ‎（2），.‎ ‎18. （1）2,1,2； （2）.‎ ‎19. （1），； （2）.‎ ‎20. （1）a=0.014，众数95，中位数； （2）.‎ ‎21. （1），图象（略）；（2），最小值，时取到.‎ ‎22. （1）； （2）.‎