河南省六市2020届高三模拟调研数学（文）试题 12页

‎★‎‎2020年5月28日 ‎2020年河南省六市高三第二次联合调研检测 数学（理科）‎ 本试卷分第Ⅰ卷（选择题）和第II卷（非选择题）两部分，满分150分，考试用时120分钟．其中第I1卷22题，23题为选考题，其它题为必考题。考试结束后，将答题卡交回.‎ 注意事项:‎ ‎1．答题前，考生必须将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内.‎ ‎2．选择题必须用2B铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚.‎ ‎3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效．‎ ‎4．保持卡面清洁，不要折叠、不要弄破、不准使用涂改液、刮纸刀．‎ 第I卷 选择题（共60分）‎ 一、选择题：本题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。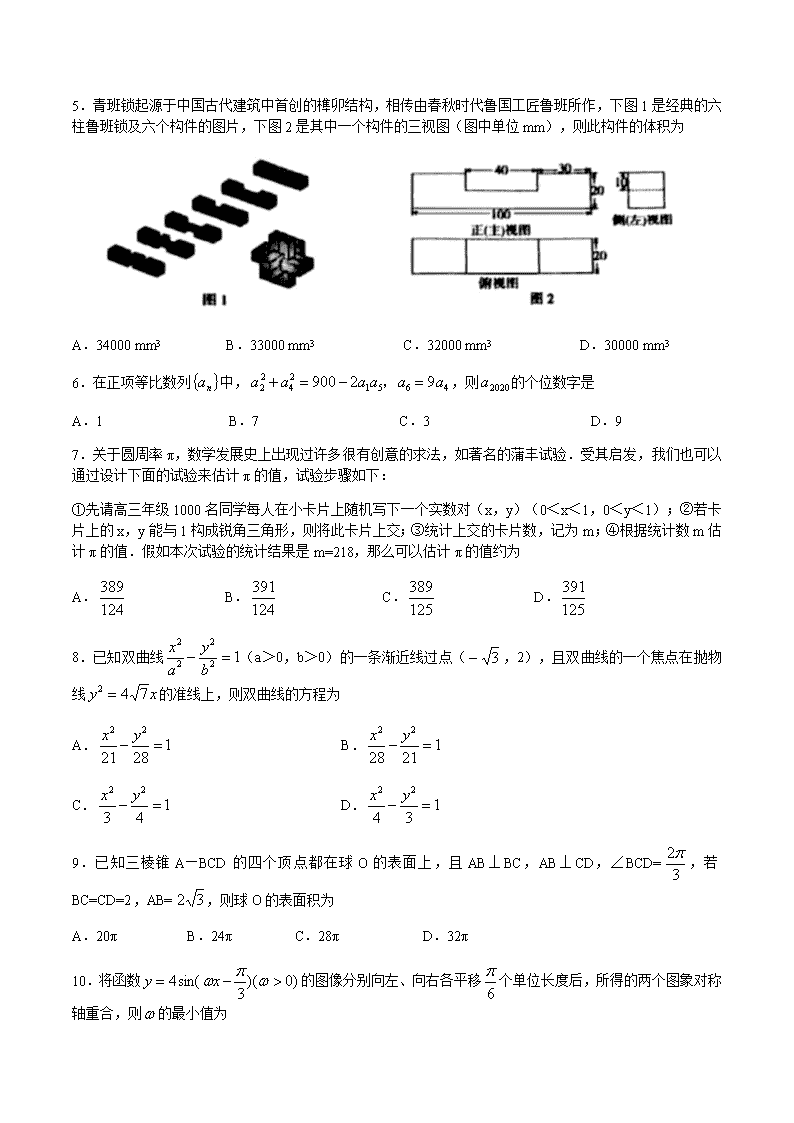‎ ‎1．设全集U=R，集合，则=‎ A．（，4] B．[，4） C．（，4） D．[，4]‎ ‎2．复数z1在复平面内对应的点为（2，3）．（i为虚数单位），则复数的虚部为 A． B． C． D．‎ ‎3．在△ABC中，若点D满足，则=‎ A． B． C． D． ‎ ‎4．南北朝时代的伟大科学家祖暅在数学上有突出贡献，他在实践的基础上提出祖暅原理：“幂势既同，则积不容异”．其含义是：夹在两个平行平面之间的两个几何体，被平行于这两个平行平面的任意平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等，如图，夹在两个平行平面之间的两个几何体的体积分别为V1，V2，被平行于这两个平面的任意平面截得的两个截面面积分别为S1、S2，则“S1、S2不总相等”是“V1，V2不相等”的 A．充分而不必要条件 ‎ B．必要而不充分条件 C．充分必要条件 ‎ D．既不充分也不必要条件 ‎5．青班锁起源于中国古代建筑中首创的榫卯结构，相传由春秋时代鲁国工匠鲁班所作，下图1是经典的六柱鲁班锁及六个构件的图片，下图2是其中一个构件的三视图（图中单位mm），则此构件的体积为 A．‎34000 mm3 B．‎33000 mm3 C．‎32000 mm3 D．‎30000 mm3 ‎ ‎6．在正项等比数列中，，则的个位数字是 A．1 B．‎7 C．3 D．9‎ ‎7．关于圆周率π，数学发展史上出现过许多很有创意的求法，如著名的蒲丰试验．受其启发，我们也可以通过设计下面的试验来估计π的值，试验步骤如下：‎ ‎①先请高三年级1000名同学每人在小卡片上随机写下一个实数对（x，y）（0＜x＜1，0＜y＜1）；②若卡片上的x，y能与1构成锐角三角形，则将此卡片上交；③统计上交的卡片数，记为m；④根据统计数m估计π的值．假如本次试验的统计结果是m=218，那么可以估计π的值约为 A． B． C． D．‎ ‎8．已知双曲线（a＞0，b＞0）的一条渐近线过点（，2），且双曲线的一个焦点在抛物线的准线上，则双曲线的方程为 A． B． ‎ C． D．‎ ‎9．已知三棱锥A—BCD的四个顶点都在球O的表面上，且AB⊥BC，AB⊥CD，∠BCD=，若BC=CD=2，AB=，则球O的表面积为 A．20π B．24π C．28π D．32π ‎10．将函数的图像分别向左、向右各平移个单位长度后，所得的两个图象对称轴重合，则的最小值为 A．3 B．‎2 C．4 D．6‎ ‎11．已知函数y=f（x）满足f（x+1）=f（x-1），当x∈[-1，1]时f（x）=x2，则方程实根共有 A．10个 B．9个 C．18个 D．20个 ‎12．已知椭圆C1：（a＞b＞0）与圆C2：，若在椭圆C1上不存在点P，使得由点P所作的圆C2的两条切线互相垂直，则椭圆C1的离心率的取值范围是 A． B． C． D．‎ 第Ⅱ卷 非选择题（共90分）‎ 二、填空题：本题共4个小题，每小题5分，共20分．‎ ‎13．已知函数的图像在点（1，）处的切线过点（2，11），则a= ．‎ ‎14．若实数x，y满足约束条件工，则z=5x +y的最小值为 ．‎ ‎15．设函数，则不等式的解集是 ．（用区间表示）‎ ‎16．在△ABC中，内角A，B，C所对的边分别是a，b，c，且BC边上的高为，则的最大值是 ．‎ 三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．‎ ‎17．（本小题满分12分）‎ 已知数列{an}满足：（n∈N+）．‎ ‎（Ⅰ）求{an}的通项公式；‎ ‎（Ⅱ）设，若数列{bn}的前n项和为，求满足的最小正整数n．‎ ‎18．（本小题满分12分）‎ 在直角梯形ABCD中（如图1），AB∥DC，∠BAD =90°，AB=5，AD =2，CD=3，点E在CD上，且DE=2，将△ADE沿AE折起，使得平面ADE⊥平面ABCE（如图2），G为AE中点．‎ ‎（Ⅰ）求四棱锥D—ABCE的体积；‎ ‎（Ⅱ）在线段BD上是否存在点P，使得CP∥平面ADE？若存在，求的值；若不存在，请说明理由．‎ ‎19．（本小题满分12分）‎ 某快递公司招聘快递骑手，该公司提供了两种日工资方案：方案（1）规定每日底新50元，快递骑手每完成一单业务提成3元：方案（2）规定每日底薪100元，快递业务的前44单没有提成，从第45单开始，每完成一单提成5元．该快递公司记录了每天骑手的人均业务量．现随机抽取100天的数据，将样本数据分为[25，35），[35，45），[45，55），[55，65），[65，75），[75，85），[85，95] 七组，整理得到如图所示的频率分布直方图．‎ ‎（Ⅰ）随机选取一天，估计这一天该快递公司的骑手的人均日快递业务量不少于65单的概率；‎ ‎（Ⅱ）若骑手甲、乙、丙选择了日工资方案（1），丁、戊选择了日工资方案（2）．现从上述5名骑手中随机选取2人，求至少有1名骑手选择方案（2）的概率；‎ ‎（Ⅲ）若仅从人均日收入的角度考虑，请你利用所学的统计学知识为新聘骑手做出日工资方案的选择，并说明理由（同组中的每个数据用该组区间的中点值代替）‎ ‎20．（本小题满分12分）‎ 设函数．‎ ‎（Ⅰ）若当x=1时取得极值，求a的值及的单调区间；‎ ‎（Ⅱ）若存在两个极值点，，证明：．‎ ‎21．（本小题满分12分）‎ 已知圆F：，动点Q（x≥0），线段QF与圆F相交于点P，线段PQ的长度与点Q到y轴的距离相等．‎ ‎（Ⅰ）求动点Q的轨迹W的方程；‎ ‎（Ⅱ）过点A（2，4）作两条互相垂直的直线与W的交点分别是M和N（M在N的上方，A，M，N为不同的三点），求向量在y轴正方向上的投影的取值范围．‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题计分．‎ ‎22．（本小题满分10分）‎ 在直角坐标系xOy中，曲线C1的参数方程为（t为参数），以原点O为极点，以x轴正半轴为极轴，建立极坐标系，曲线C2的极坐标方程为．‎ ‎（Ⅰ）求曲线C1的极坐标方程与曲线C2的直角坐标方程；‎ ‎（Ⅱ）设A．B为曲线C2上位于第一，二象限的两个动点，且∠AOB=，射线OA，OB交曲线C1分别于点D，C．求△AOB面积的最小值，并求此时四边形ABCD的面积。‎ ‎23．（本小题满分10分）‎ 已知a，b，c均为正实数，函数的最小值为1．‎ 证明：（Ⅰ）；‎ ‎（Ⅱ）．‎