2018届二轮复习方法指导-空间向量与立体几何课件（全国通用） 42页

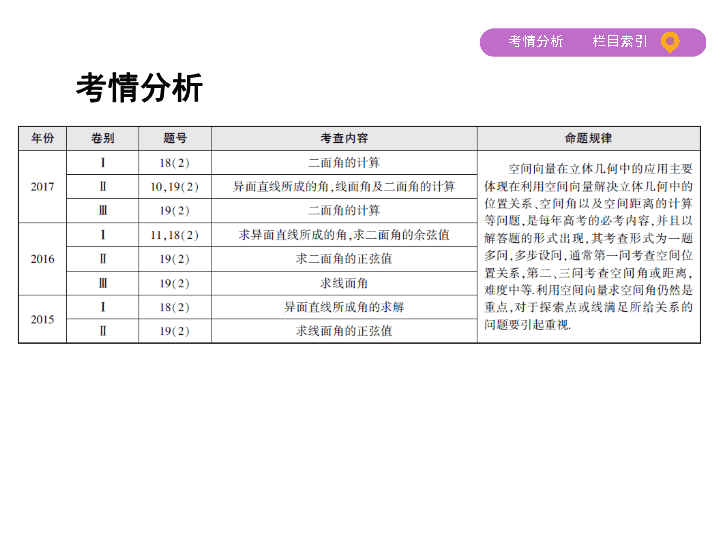
第 3 讲 空间向量与立体几何 考情分析 总纲目录 考点一   向量法证明平行与垂直 考点二 利用空间向量求空间角（高频考点） 考点三 立体几何中的探索性问题 考点一  向量法证明平行与垂直 设直线 l 的方向向量为 a =( a 1 , b 1 , c 1 ),平面 α 、 β 的法向量分别为 μ =( a 2 , b 2 , c 2 ), v =( a 3 , b 3 , c 3 ). (1)线面平行 l ∥ α ⇔ a ⊥ μ ⇔ a · μ =0 ⇔ a 1 a 2 + b 1 b 2 + c 1 c 2 =0. (2)线面垂直 l ⊥ α ⇔ a ∥ μ ⇔ a = kμ ⇔ a 1 = ka 2 , b 1 = kb 2 , c 1 = kc 2 ( k ≠ 0). (3)面面平行 α ∥ β ⇔ μ ∥ v ⇔ μ = λv ⇔ a 2 = λa 3 , b 2 = λb 3 , c 2 = λc 3 ( λ ≠ 0). (4)面面垂直 α ⊥ β ⇔ μ ⊥ v ⇔ μ · v =0 ⇔ a 2 a 3 + b 2 b 3 + c 2 c 3 =0. 典型例题 　　如图所示,在底面是矩形的四棱锥 P - ABCD 中, PA ⊥底面 ABCD , E , F 分别是 PC , PD 的中点, PA = AB =1, BC =2. (1)求证: EF ∥平面 PAB ; (2)求证:平面 PAD ⊥平面 PDC .   证明 　以 A 为坐标原点, AB , AD , AP 所在直线分别为 x 轴, y 轴, z 轴,建立空间 直角坐标系如图所示,则 A (0,0,0), B (1,0,0), C (1,2,0), D (0,2,0), P (0,0,1),   所以 E   , F   ,   =   ,   =(0,0,1),   =(0,2,0),   =(1,0, 0),   =(1,0,0). (1)因为   =-     ,所以   ∥   , 即 EF ∥ AB . 又 AB ⊂ 平面 PAB , EF ⊄ 平面 PAB , 所以 EF ∥平面 PAB . (2)因为   ·   =(0,0,1)·(1,0,0)=0,   ·   =(0,2,0)·(1,0,0)=0, 所以   ⊥   ,   ⊥   , 即 AP ⊥ DC , AD ⊥ DC . 又因为 AP ∩ AD = A , AP ⊂ 平面 PAD , AD ⊂ 平面 PAD , 所以 DC ⊥平面 PAD .因为 DC ⊂ 平面 PDC , 所以平面 PAD ⊥平面 PDC . 方法归纳 向量法证明平行与垂直的四个步骤 (1)建立空间直角坐标系,建系时,要尽可能地利用已知的垂直关系; (2)建立空间图形与空间向量之间的关系,用空间向量表示出问题中所 涉及的点、直线、平面; (3)通过空间向量的运算求出平面向量或法向量,再研究平行、垂直关 系; (4)根据运算结果解释相关问题. 跟踪集训 　在直三棱柱 ABC - A 1 B 1 C 1 中,∠ ABC =90 ° , BC =2, CC 1 =4,点 E 在线段 BB 1 上, 且 EB 1 =1, D , F , G 分别为 CC 1 , C 1 B 1 , C 1 A 1 的中点.求证: (1) B 1 D ⊥平面 ABD ; (2)平面 EGF ∥平面 ABD .   则 B (0,0,0), D (0,2,2), B 1 (0,0,4), C 1 (0,2,4), 设 BA = a ( a >0),则 A ( a ,0,0), 所以   =( a ,0,0),   =(0,2,2),   =(0,2,-2), 所以   ·   =0,   ·   =0+4-4=0, 即 B 1 D ⊥ BA , B 1 D ⊥ BD . 又 BA ∩ BD = B , BA , BD ⊂ 平面 ABD , 因此 B 1 D ⊥平面 ABD . 证明 　 (1) 以 B 为坐标原点 , BA , BC , BB 1 所在的直线分别为 x 轴 , y 轴 , z 轴建立 空间直角坐标系 , 如图所示 , (2)由(1),知 E (0,0,3), G   , F (0,1,4), 则   =   ,   =(0,1,1), 所以   ·   =0+2-2=0,   ·   =0+2-2=0, 即 B 1 D ⊥ EG , B 1 D ⊥ EF . 又 EG ∩ EF = E , EG , EF ⊂ 平面 EGF , 因此 B 1 D ⊥平面 EGF . 结合(1)可知平面 EGF ∥平面 ABD . 考点二  利用空间向量求空间角(高频考点) 命题点 1.利用空间向量求线线角、线面角、二面角. 2.由空间角的大小求参数值或线段长. 1.向量法求异面直线所成的角 若异面直线 a , b 的方向向量分别为 a , b ,所成的角为 θ ,则cos θ =|cos< a , b >|=   . 2.向量法求线面所成的角 求出平面的法向量 n ,直线的方向向量 a ,设线面所成的角为 θ ,则sin θ =|cos < n , a >|=   . 3.向量法求二面角 求出二面角 α - l - β 的两个半平面 α 与 β 的法向量 n 1 , n 2 ,若二面角 α - l - β 所成的 角 θ 为锐角,则cos θ =|cos< n 1 , n 2 >|=   ; 若二面角 α - l - β 所成的角 θ 为钝角,则cos θ =-|cos< n 1 , n 2 >|=-   . 典型例题 (2017课标全国Ⅱ,19,12分)如图,四棱锥 P - ABCD 中,侧面 PAD 为等边三角 形且垂直于底面 ABCD , AB = BC =   AD ,∠ BAD =∠ ABC =90 ° , E 是 PD 的中点. (1)证明:直线 CE ∥平面 PAB ; (2)点 M 在棱 PC 上,且直线 BM 与底面 ABCD 所成角为45 ° ,求二面角 M - AB - D 的余弦值. 解析 　(1)取 PA 的中点 F ,连接 EF , BF . 因为 E 是 PD 的中点,所以 EF ∥ AD , EF =   AD . 由∠ BAD =∠ ABC =90 ° 得 BC ∥ AD ,又 BC =   AD ,所以 EF