2018届二轮复习（理）专题一　函数与导数、不等式第1讲课件（全国通用） 32页

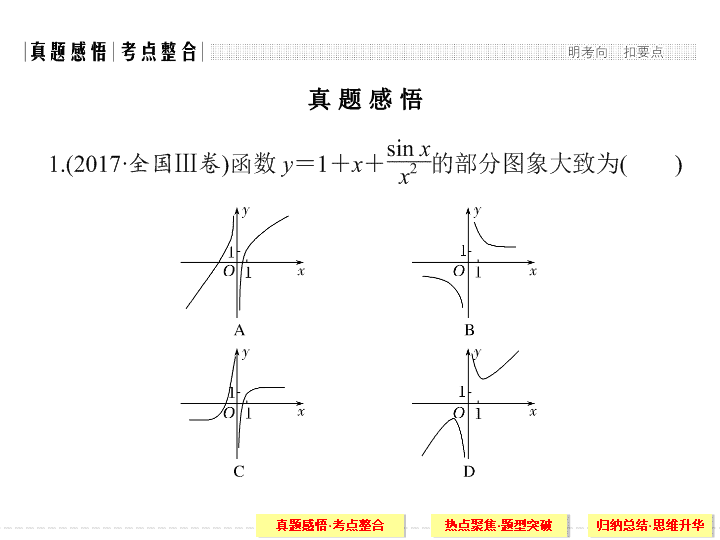
第 1 讲　函数图象与性质 高考定位　 1. 以基本初等函数为载体 ， 考查函数的定义域、最值、奇偶性、单调性和周期性； 2. 利用函数的图象研究函数性质 ， 能用函数的图象性质解决简单问题； 3. 函数与方程思想、数形结合思想是高考的重要思想方法 . 真 题 感 悟 答案 　 D 答案 　 C 3. (2017· 全国 Ⅰ 卷 ) 已知函数 f ( x ) 在 ( － ∞ ，＋ ∞ ) 上单调递减，且为奇函数 . 若 f (1) ＝－ 1 ，则满足－ 1 ≤ f ( x － 2) ≤ 1 的 x 的取值范围是 ( 　　 ) A.[ － 2 ， 2] B.[ － 1 ， 1] C.[0 ， 4] D.[1 ， 3] 解析 　 因为 f ( x ) 为奇函数 ， 所以 f ( － 1) ＝－ f (1) ＝ 1 ， 于是－ 1 ≤ f ( x － 2) ≤ 1 等价于 f (1) ≤ f ( x － 2) ≤ f ( － 1) ， 又 f ( x ) 在 ( － ∞ ， ＋ ∞ ) 上单调递减 ， ∴ － 1 ≤ x － 2 ≤ 1 ，∴ 1 ≤ x ≤ 3. 答案 　 D 答案　 B 1. 函数的性质 (1) 单调性：单调性是函数在其定义域上的局部性质 . 证明函数的单调性时，规范步骤为取值、作差、变形、判断符号和下结论 . 复合函数的单调性遵循 “ 同增异减 ” 的原则 . (2) 奇偶性： ① 若 f ( x ) 是偶函数，则 f ( x ) ＝ f ( － x ). ② 若 f ( x ) 是奇函数， 0 在其定义域内，则 f (0) ＝ 0. ③ 奇函数在关于原点对称的单调区间内有相同的单调性，偶函数在关于原点对称的单调区间内有相反的单调性 . (3) 周期性： ① 若 y ＝ f ( x ) 对 x ∈ R ， f ( x ＋ a ) ＝ f ( x － a ) 或 f ( x ＋ 2 a ) ＝ f ( x )( a >0) 恒成立，则 y ＝ f ( x ) 是周期为 2 a 的周期函数 . 考 点 整 合 易错提醒 　 错用集合运算符号致误：函数的多个单调区间若不连续 ， 不能用符号 “ ∪ ” 连接 ， 可用 “ 和 ” 或 “ ，” 连接 . 2. 函数的图象 (1) 对于函数的图象要会作图、识图和用图，作函数图象有两种基本方法：一是描点法；二是图象变换法，其中图象变换有平移变换、伸缩变换和对称变换 . (2) 在研究函数性质特别是单调性、值域、零点时，要注意结合其图象研究 . (3) 函数图象的对称性 ① 若函数 y ＝ f ( x ) 满足 f ( a ＋ x ) ＝ f ( a － x ) ，即 f ( x ) ＝ f (2 a － x ) ，则 y ＝ f ( x ) 的图象关于直线 x ＝ a 对称； ② 若函数 y ＝ f ( x ) 满足 f ( a ＋ x ) ＝－ f ( a － x ) ，即 f ( x ) ＝－ f (2 a － x ) ，则 y ＝ f ( x ) 的图象关于点 ( a ， 0) 对称 . 热点一　函数及其表示 答案　 (1)C 　 (2)A 探究提高　 1.(1) 给出解析式的函数的定义域是使解析式有意义的自变量的集合 ， 只需构建不等式 ( 组 ) 求解即可 . (2) 抽象函数：根据 f ( g ( x )) 中 g ( x ) 的范围与 f ( x ) 中 x 的范围相同求解 . 2. 对于分段函数的求值问题 ， 必须依据条件准确地找出利用哪一段求解；形如 f ( g ( x )) 的函数求值时 ， 应遵循先内后外的原则 . 答案　 (1)C 　 (2)A 热点二　函数的图象及应用 命题角度 1 　函数图象的识别 答案　 A 命题角度 2 　函数图象的应用 【例 2 － 2 】 (1) (2017· 历城冲刺 ) 已知 f ( x ) ＝ 2 x － 1 ， g ( x ) ＝ 1 － x 2 ，规定：当 | f ( x )| ≥ g ( x ) 时， h ( x ) ＝ | f ( x )| ；当 | f ( x )| ＜ g ( x ) 时， h ( x ) ＝－ g ( x ) ，则 h ( x )( 　　 ) A. 有最小值－ 1 ，最大值 1 B. 有最大值 1 ，无最小值 C. 有最小值－ 1 ，无最大值 D. 有最大值－ 1 ，无最小值 解析　 (1) 画出 y ＝ | f ( x )| ＝ |2 x － 1| 与 y ＝ g ( x ) ＝ 1 － x 2 的图象 ， 它们交于 A ， B 两点 . 由 “ 规定 ” ， 在 A ， B 两侧 ， | f ( x )| ≥ g ( x ) ， 故 h ( x ) ＝ | f ( x )| ；在 A ， B 之间 ， | f ( x )|< g ( x ) ， 故 h ( x ) ＝－ g ( x ). 综上可知 ， y ＝ h ( x ) 的图象是图中的实线部分 ， 因此 h ( x ) 有最小值－ 1 ， 无最大值 . 答案　 (1)C 　 (2)D 探究提高　 1. 已知函数的解析式 ， 判断其图象的关键是由函数解析式明确函数的定义域、值域、单调性、奇偶性、周期性等 ， 以及函数图象上的特殊点 ，根据这些性质对函数图象进行具体分 析判断 . 2 . (1) 运用函数图象解决问题时 ， 先要正确理解和把握函数图象本身的含义及其表示的内容 ， 熟悉图象所能够表达的函数的性质 .(2) 图象形象地显示了函数的性质 ， 因此 ， 函数性质的确定与应用及一些方程、不等式的求解常与图象数形结合研究 . (2) 函数 y ＝ | f ( x )| 的图象如图 . y ＝ ax 为过原点的一条直线 ，当 a >0 时 ， 与 y ＝ | f ( x )| 在 y 轴右侧总有交点 ， 不合题意；当 a ＝ 0 时成立；当 a <0 时 ， 找与 y ＝ | － x 2 ＋ 2 x |( x ≤ 0) 相切的情况 ， 即 y ′ ＝ 2 x － 2 ， 切点为 (0 ， 0) ， 此时 a ＝ 2 × 0 － 2 ＝－ 2 ， 即有－ 2 ≤ a <0 ， 综上 ， a ∈ [ － 2 ， 0]. 答案　 (1)A 　 (2)D 热点三　函数的性质与应用 【例 3 】 (1) (2017· 山东卷 ) 已知 f ( x ) 是定义在 R 上的偶函数，且 f ( x ＋ 4) ＝ f ( x － 2). 若当 x ∈ [ － 3 ， 0] 时， f ( x ) ＝ 6 － x ，则 f (919) ＝ ________. (2) (2017· 天津卷 ) 已知奇函数 f ( x ) 在 R 上是增函数， g ( x ) ＝ xf ( x ). 若 a ＝ g ( － log 2 5.1) ， b ＝ g (2 0.8 ) ， c ＝ g (3) ，则 a ， b ， c 的大小关系为 ( 　　 ) A. a < b < c B. c < b < a C. b < a < c D. b < c < a 解析 　 (1) ∵ f ( x ＋ 4) ＝ f ( x － 2) ，∴ f [( x ＋ 2) ＋ 4] ＝ f [( x ＋ 2) － 2] ， 即 f ( x ＋ 6) ＝ f ( x ) ， ∴ f (919) ＝ f (153 × 6 ＋ 1) ＝ f (1) ， 又 f ( x ) 在 R 上是偶函数 ， ∴ f (1) ＝ f ( － 1) ＝ 6 － ( － 1) ＝ 6 ， 即 f (919) ＝ 6. (2) 法一 　 易知 g ( x ) ＝ xf ( x ) 在 R 上为偶函数 ， ∵ 奇函数 f ( x ) 在 R 上是增函数 ， 且 f (0) ＝ 0. ∴ g ( x ) 在 (0 ， ＋ ∞ ) 上是增函数 . 又 3>log 2 5.1>2>2 0.8 ， 且 a ＝ g ( － log 2 5.1) ＝ g (log 2 5.1) ， ∴ g (3)> g (log 2 5.1)> g (2 0.8 ) ， 则 c > a > b . 法二 　 ( 特殊化 ) 取 f ( x ) ＝ x ， 则 g ( x ) ＝ x 2 为偶函数且在 (0 ， ＋ ∞ ) 上单调递增 ， 又 3>log 2 5.1>2 0.8 ， 从而可得 c > a > b . 答案 　 (1)6 　 (2)C 探究提高　 1. 利用函数的奇偶性和周期性可以转化函数的解析式、图象和性质 ， 把不在已知区间上的问题 ， 转化到已知区间上求解 . 2 . 函数单调性应用：可以比较大小、求函数最值、解不等式、证明方程根的唯一性 . 答案　 (1) － 8 　 (2)D 3. 三种作函数图象的基本思想方法 (1) 通过函数图象变换利用已知函数图象作图； (2) 对函数解析式进行恒等变换，转化为已知方程对应的曲线； (3) 通过研究函数的性质，明确函数图象的位置和形状 . 4. 函数是中学数学的核心，函数思想是重要的思想方法，利用函数思想研究方程 ( 不等式 ) 才能抓住问题的本质，对于给定的函数若不能直接求解或画出图形，常会通过分解转化为两个函数图象，数形结合直观求解 .