【数学】2019届一轮复习人教A版两角和与差的正弦、余弦和正切公式学案 20页

第五节两角和与差的正弦、余弦和正切公式 ‎1．两角和与差的正弦、余弦和正切公式 sin(α±β)＝sin_αcos_β±cos_αsin_β；‎ cos(α∓β)＝cos_αcos_β±sin_αsin_β；‎ tan(α±β)＝.‎ ‎2．二倍角的正弦、余弦、正切公式 sin 2α＝2sin_αcos_α；‎ cos 2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α；‎ tan 2α＝.‎ ‎3．公式的常用变形 ‎(1)tan α±tan β＝tan(α±β)(1∓tan αtan β)；‎ ‎(2)cos2α＝，sin2α＝；‎ ‎(3)1＋sin 2α＝(sin α＋cos α)2，‎ ‎1－sin 2α＝(sin α－cos α)2，‎ sin α±cos α＝sin.‎ ‎1．判断下列结论是否正确(请在括号中打“√”或“×”)‎ ‎(1)两角和与差的正弦、余弦公式中的角α，β是任意的．(　　)‎ ‎(2)存在实数α，β，使等式sin(α＋β)＝sin α＋sin β成立．(　　)‎ ‎(3)公式tan(α＋β)＝可以变形为tan α＋tan β＝tan(α＋β)(1－tan αtan β)，且对任意角α，β都成立．(　　)‎ ‎(4)存在实数α，使tan 2α＝2tan α.(　　)‎ 答案：(1)√　(2)√　(3)×　(4)√‎ ‎2．sin 20°cos 10°－cos 160°sin 10°＝(　　)‎ A．－　　　　　　　　 B. C．－ D. 解析：选D　原式＝sin 20°cos 10°＋cos 20°sin 10°＝sin(20°＋10°)＝sin 30°＝，故选D.‎ ‎3．设角θ的终边过点(2,3)，则tan＝(　　)‎ A. B．－ C．5 D．－5‎ 解析：选A　由于角θ的终边过点(2,3)，因此tan θ＝，故tan＝＝＝，选A.‎ ‎4．(2017·山东高考)已知cos x＝，则cos 2x＝(　　)‎ A．－ B. C．－ D. 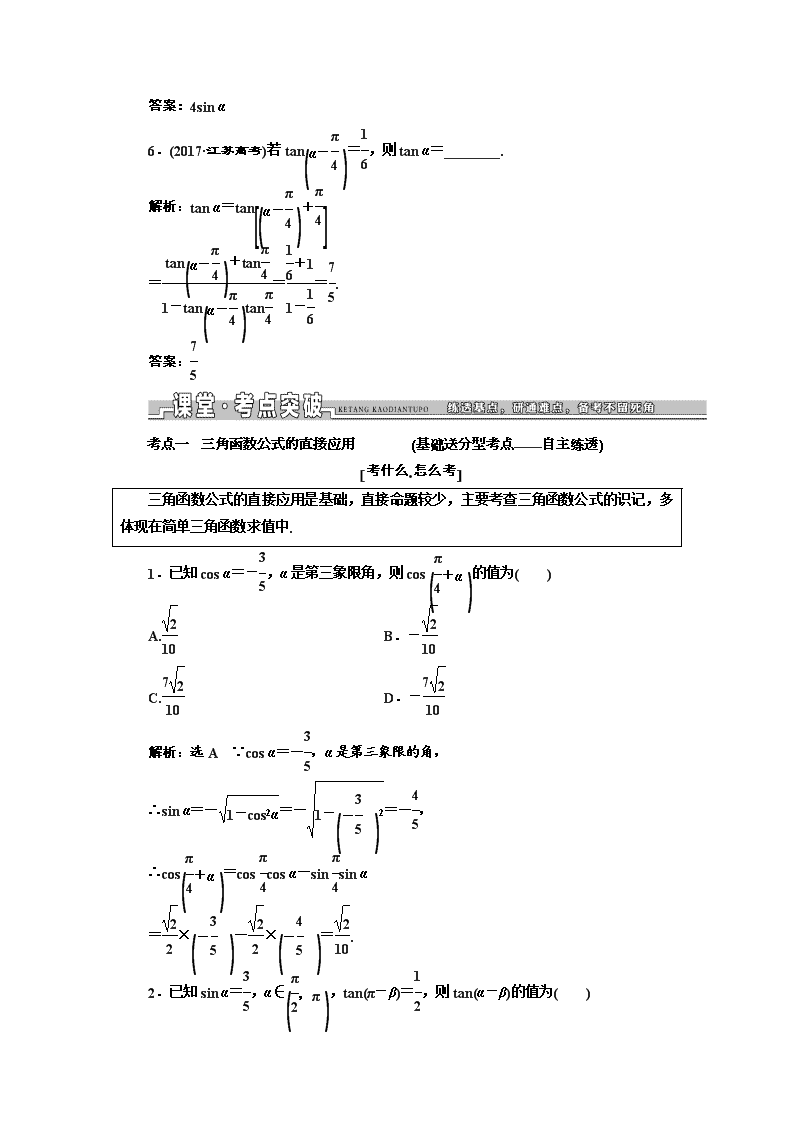解析：选D　∵cos x＝，∴cos 2x＝2cos2x－1＝.‎ ‎5．化简：＝________.‎ 解析：＝ ‎＝＝4sin α.‎ 答案：4sin α ‎6．(2017·江苏高考)若tan＝，则tan α＝________.‎ 解析：tan α＝tan ‎＝＝＝.‎ 答案： 　　　　 ‎[考什么·怎么考]‎ 三角函数公式的直接应用是基础，直接命题较少，主要考查三角函数公式的识记，多体现在简单三角函数求值中.‎ ‎1．已知cos α＝－，α是第三象限角，则cos的值为(　　)‎ A.　　　　　　　　 B．－ C. D．－ 解析：选A　∵cos α＝－，α是第三象限的角，‎ ‎∴sin α＝－＝－＝－，‎ ‎∴cos＝cos cos α－sin sin α ‎＝×－×＝.‎ ‎2．已知sin α＝，α∈，tan(π－β)＝，则tan(α－β)的值为(　　)‎ A．－ B. C. D．－ 解析：选A　因为sin α＝，α∈，‎ 所以cos α＝－＝－，‎ 所以tan α＝＝－.‎ 因为tan(π－β)＝＝－tan β，所以tan β＝－，‎ 则tan(α－β)＝＝－.‎ ‎3．已知α∈，sin α＝，则cos的值为______．‎ 解析：因为α∈，sin α＝，‎ 所以cos α＝－＝－.‎ sin 2α＝2sin αcos α＝2××＝－，‎ cos 2α＝1－2sin2α＝1－2×2＝，‎ 所以cos＝coscos 2α＋sin sin 2α ‎＝×＋× ‎＝－.‎ 答案：－ ‎[怎样快解·准解]‎ 三角函数公式的应用策略 ‎(1)使用两角和与差的三角函数公式，首先要记住公式的结构特征．‎ ‎(2)使用公式求值，应先求出相关角的函数值，再代入公式求值．‎ 　　　　 ‎[考什么·怎么考]‎ 主要考查对三角函数公式的熟练掌握程度，对公式结构的准确理解和记忆.‎ 考法(一)　三角函数公式的逆用 ‎1.＝________.‎ 解析：＝＝＝＝.‎ 答案： ‎2．在△ABC中，若tan Atan B＝ tan A＋tan B＋1, 则cos C＝________.‎ 解析：由tan Atan B＝tan A＋tan B＋1，可得＝－1，即tan(A＋B)＝－1，又A＋B∈(0，π)，所以A＋B＝，则C＝，cos C＝.‎ 答案： ‎3．已知cos＋sin α＝，则sin＝________.‎ 解析：由cos＋sin α＝，‎ 可得cos α＋sin α＋sin α＝，‎ 即sin α＋cos α＝，‎ ‎∴sin＝，即sin＝，‎ ‎∴sin＝－sin＝－.‎ 答案：－ 考法(二)　三角函数公式的变形用 ‎4．化简＝________.‎ 解析：＝＝＝－1.‎ 答案：－1‎ ‎5．化简sin2＋sin2－sin2α的结果是________．‎ 解析：原式＝＋－sin2α ‎＝1－－sin2α ‎＝1－cos 2α·cos －sin2α ‎＝1－－ ‎＝.‎ 答案： ‎[怎样快解·准解]‎ ‎1．注意三角函数公式逆用和变形用的2个问题 ‎(1)公式逆用时一定要注意公式成立的条件和角之间的关系．‎ ‎(2)注意特殊角的应用，当式子中出现，1，，等这些数值时，一定要考虑引入特殊角，把“值变角”构造适合公式的形式．‎ ‎2．熟记三角函数公式的2类变式 ‎(1)和差角公式变形：‎ sin αsin β＋cos(α＋β)＝cos αcos β，‎ cos αsin β＋sin(α－β)＝sin αcos β，‎ tan α±tan β＝tan(α±β)·(1∓tan α·tan β)．‎ ‎(2)倍角公式变形：‎ 降幂公式cos2α＝，sin2α＝，‎ 配方变形：1±sin α＝2,1＋cos α＝2cos2，1－cos α＝2sin2.‎ 　　　　 三角函数公式中角的变换与名的变换在三角函数求值中经常考查，题目难度不大，属于中低档题.‎ ‎[典题领悟]‎ ‎1．(2018·南充模拟)已知α∈，β∈，且cos α＝，cos(α＋β)＝－，则sin β＝________.‎ 解析：因为α∈，β∈，且cos α＝，cos(α＋β)＝－，所以α＋β∈(0，π)，‎ 所以sin α＝＝，‎ sin(α＋β)＝＝，‎ 则sin β＝sin[(α＋β)－α]‎ ‎＝sin(α＋β)cos α－cos(α＋β)sin α ‎＝×－×＝.‎ 答案： ‎2．已知tan(α＋β)＝，tan β＝，则tan(α－β)的值为________．‎ 解析：∵tan(α＋β)＝，tan β＝，‎ ‎∴tan α＝tan[(α＋β)－β]＝＝＝，‎ tan(α－β)＝＝＝－.‎ 答案：－ ‎[解题师说]‎ ‎1．迁移要准 ‎(1)看到角的范围及余弦值想到正弦值；看到β，α＋β，α想到凑角β＝(α＋β)－α，代入公式求值．‎ ‎(2)看到两个角的正切值想到两角和与差的正切公式；看到α＋β，β，α－β想到凑角．‎ ‎2．思路要明 ‎(1)角的变换：明确各个角之间的关系(包括非特殊角与特殊角、已知角与未知角)，熟悉角的拆分与组合的技巧，半角与倍角的相互转化，如：2α＝(α＋β)＋(α－β)，α＝(α＋β)－β＝(α－β)＋β，40°＝60°－20°，＋＝，＝2×等．‎ ‎(2)名的变换：明确各个三角函数名称之间的联系，常常用到同角关系、诱导公式，把正弦、余弦化为正切，或者把正切化为正弦、余弦．‎ ‎3．思想要有 转化思想是实施三角变换的主导思想，恒等变形前需清楚已知式中角的差异、函数名称的差异、运算结构的差异，寻求联系，实现转化．‎ ‎[冲关演练]‎ ‎1．(2017·全国卷Ⅰ)已知α∈，tan α＝2，则cos＝________.‎ 解析：∵α∈，tan α＝2，‎ ‎∴sin α＝，cos α＝，‎ ‎∴cos＝cos αcos＋sin αsin ‎＝×＝.‎ 答案： ‎2．已知α，β均为锐角，且sin α＝，tan(α－β)＝－.‎ ‎(1)求sin(α－β)的值；‎ ‎(2)求cos β的值．‎ 解：(1)∵α，β∈，从而－<α－β<.‎ 又∵tan(α－β)＝－<0，‎ ‎∴－<α－β<0.‎ ‎∴sin(α－β)＝－.‎ ‎(2)由(1)可得，cos(α－β)＝.‎ ‎∵α为锐角，且sin α＝，∴cos α＝.‎ ‎∴cos β＝cos[α－(α－β)]＝cos αcos(α－β)＋sin αsin(α－β)‎ ‎＝×＋×＝.‎ ‎(一)普通高中适用作业 A级——基础小题练熟练快 ‎1．sin 45°cos 15°＋cos 225°sin 165°＝(　　)‎ A．1　　　　　　　　　　 B. C. D．－ 解析：选B　sin 45°cos 15°＋cos 225°sin 165°＝sin 45°·cos 15°＋(－cos 45°)sin 15°＝sin(45°－15°)＝sin 30°＝.‎ ‎2．若2sin＝3sin(π－θ)，则tan θ等于(　　)‎ A．－ B. C. D．2 解析：选B　由已知得sin θ＋cos θ＝3sin θ，‎ 即2sin θ＝cos θ，所以tan θ＝.‎ ‎3．(2018·石家庄质检)若sin(π－α)＝，且≤α≤π，则sin 2α的值为(　　)‎ A．－ B．－ C. D. 解析：选A　因为sin(π－α)＝sin α＝，≤α≤π，所以cos α＝－，所以sin 2α＝2sin αcos α＝2××＝－.‎ ‎4．(2018·衡水调研)若α∈，且3cos 2α＝sin，则sin 2α的值为(　　)‎ A．－ B. C．－ D. 解析：选C　由3cos 2α＝sin，可得3(cos2α－sin2α)＝(cos α－sin α)，又由α∈，可知cos α－sin α≠0，于是3(cos α＋sin α)＝，所以1＋2sin αcos α＝，故sin 2α＝－.‎ ‎5．计算的值为(　　)‎ A．－ B. ‎ C. D．－ 解析：选B　＝ ‎＝＝＝.‎ ‎6．(2017·全国卷Ⅲ)函数f(x)＝sin＋cos的最大值为(　　)‎ A. B．1‎ C. D. 解析：选A　因为cos＝cos＝sin，所以f(x)＝sin，于是f(x)的最大值为.‎ ‎7．已知sin＝，α∈，则cos的值为________．‎ 解析：由已知得cos α＝，sin α＝－，‎ 所以cos＝cos α＋sin α＝－.‎ 答案：－ ‎8．(2018·贵州适应性考试)已知α是第三象限角，且cos(α＋π)＝，则tan 2α＝________.‎ 解析：由cos(α＋π)＝－cos α＝，得cos α＝－，又α是第三象限角，所以sin α＝－，tan α＝，故tan 2α＝＝.‎ 答案： ‎9．已知cos＝－，则cos x＋cos＝________.‎ 解析：cos x＋cos ‎＝cos x＋cos x＋sin x ‎＝cos x＋sin x ‎＝cos ‎＝× ‎＝－1.‎ 答案：－1‎ ‎10．(2018·石家庄质检)已知α∈，cos＝－，则cos α＝________.‎ 解析：因为α∈，所以α＋∈，‎ 所以sin＝，‎ 所以cos α＝cos＝coscos＋sinsin＝－×＋×＝.‎ 答案： B级——中档题目练通抓牢 ‎1．(2018·陕西高三教学质量检测)已知角α的终边过点P(4，－3)，则cos的值为(　　)‎ A．－ B. C．－ D. 解析：选B　由于角α的终边过点P(4，－3)，则cos α＝＝，sin α＝＝－，故cos＝cos αcos－sin αsin＝×－×＝.‎ ‎2．设α为锐角，若cos＝，则sin的值为(　　)‎ A. B. C．－ D．－ 解析：选B　因为α为锐角，且cos＝，‎ 所以sin＝ ＝，‎ 所以sin＝sin2 ‎＝2sincos＝2××＝.‎ ‎3．(2018·广东肇庆模拟)已知sin α＝且α为第二象限角，则tan＝(　　)‎ A．－ B．－ C．－ D．－ 解析：选D　由题意得cos α＝－，‎ 则sin 2α＝－，cos 2α＝2cos2α－1＝.‎ ‎∴tan 2α＝－，‎ ‎∴tan＝＝＝－.‎ ‎4．若锐角α，β满足tan α＋tan β＝－tan αtan β，则α＋β＝________.‎ 解析：由已知可得＝，即tan(α＋β)＝.‎ 又α＋β∈(0，π)，所以α＋β＝.‎ 答案： ‎5．(2018·安徽两校阶段性测试)若α∈，cos＝2cos 2α，则sin 2α＝________.‎ 解析：由已知得(cos α＋sin α)＝2(cos α－sin α)·(cos α＋sin α)，所以cos α＋sin α＝0或cos α－sin α＝，由cos α＋sin α＝0得tan α＝－1，因为α∈，所以cos α＋sin α＝0不满足条件；由cos α－sin α＝，两边平方得1－sin 2α＝，所以sin 2α＝.‎ 答案： ‎6．(2018·广东六校联考)已知函数f(x)＝sin，x∈R.‎ ‎(1)求f的值；‎ ‎(2)若cos θ ＝，θ∈，求f的值．‎ 解：(1)f＝sin＝sin＝－.‎ ‎(2)f＝sin ‎＝sin＝(sin 2θ－cos 2θ)．‎ 因为cos θ＝，θ∈，‎ 所以sin θ＝，‎ 所以sin 2θ＝2sin θcos θ＝，‎ cos 2θ＝cos2θ－sin2θ＝，‎ 所以f＝(sin 2θ－cos 2θ)‎ ‎＝×＝.‎ ‎7．已知α∈，且sin＋cos＝.‎ ‎(1)求cos α的值；‎ ‎(2)若sin(α－β)＝－，β∈，求cos β的值．‎ 解：(1)因为sin＋cos＝，‎ 两边同时平方，得sin α＝.‎ 又<α<π，所以cos α＝－＝－.‎ ‎(2)因为<α<π，<β<π，‎ 所以－<α－β<.‎ 又由sin(α－β)＝－，得cos(α－β)＝.‎ 所以cos β＝cos[α－(α－β)]‎ ‎＝cos αcos(α－β)＋sin αsin(α－β)‎ ‎＝－×＋×＝－.‎ C级——重难题目自主选做 已知coscos＝－，α∈.‎ ‎(1)求sin 2α的值；‎ ‎(2)求tan α－的值．‎ 解：(1)coscos ‎＝cossin ‎＝sin＝－，‎ 即sin＝－.‎ ‎∵α∈，∴2α＋∈，‎ ‎∴cos＝－，‎ ‎∴ sin 2α＝sin ‎＝sincos－cossin ‎＝－×－×＝.‎ ‎(2)∵α∈，∴2α∈，‎ 又由(1)知sin 2α＝，∴cos 2α＝－.‎ ‎∴tan α－＝－＝＝＝－2×＝2.‎ ‎(二)重点高中适用作业 A级——保分题目巧做快做 ‎1.计算－sin 133°cos 197°－cos 47°cos 73°的结果为(　　)‎ A.　　　　　　　　　 B. C. D. 解析：选A　－sin 133°cos 197°－cos 47°cos 73°‎ ‎＝－sin 47°(－cos 17°)－cos 47°sin 17°‎ ‎＝sin(47°－17°)＝sin 30°＝.‎ ‎2．(2018·陕西高三教学质量检测试)已知角α的终边过点P(4，－3)，则cos的值为(　　)‎ A．－ B. C．－ D. 解析：选B　由于角α的终边过点P(4，－3)，则cos α＝，sin α＝－，故cos＝cos αcos－sin αsin＝×－×＝.‎ ‎3.已知sin α＋cos α＝，则sin2＝(　　)‎ A. B. C. D. 解析：选B　由sin α＋cos α＝两边平方，得1＋sin 2α＝，解得sin 2α＝－，所以sin2＝＝＝＝.‎ ‎4．计算的值为(　　)‎ A．－ B. C. D．－ 解析：选B　＝＝＝＝.‎ ‎5.已知α∈，tan＝，那么sin 2α＋cos 2α 的值为(　　)‎ A．－ B. C．－ D. 解析：选A　由tan＝，知＝，‎ ‎∴tan 2α＝－.∵2α∈，∴sin 2α＝，cos 2α＝－，∴sin 2α＋cos 2α＝－.‎ ‎6．(2018·贵州适应性考试)已知α是第三象限角，且cos(α＋π)＝，则tan 2α＝________.‎ 解析：由cos(α＋π)＝－cos α＝，得cos α＝－，又α是第三象限角，所以sin α＝－，tan α＝，故tan 2α＝＝.‎ 答案： ‎7．已知cos＝－，则cos x＋cos＝________.‎ 解析：cos x＋cos ‎＝cos x＋cos x＋sin x ‎＝cos x＋sin x ‎＝cos ‎＝× ‎＝－1.‎ 答案：－1‎ ‎8.(2018·洛阳第一次统一考试)若sin＝，则cos＝________.‎ 解析：依题意得cos＝－cos＝－cos＝2sin2－1＝2×2－1＝－.‎ 答案：－ ‎9．已知α∈，tan α＝，求tan 2α和sin的值．‎ 解：∵tan α＝，‎ ‎∴tan 2α＝＝＝，‎ 且＝，即cos α＝2sin α，‎ 又sin2α＋cos2α＝1，‎ ‎∴5sin2α＝1，而α∈，‎ ‎∴sin α＝，cos α＝.‎ ‎∴sin 2α＝2sin αcos α＝2××＝，‎ cos 2α＝1－2sin2α＝1－2×2＝，‎ ‎∴sin＝sin 2αcos＋cos 2αsin＝×＋×＝.‎ ‎10．(2018·广东六校联考)已知函数f(x)＝sin，x∈R.‎ ‎(1)求f的值；‎ ‎(2)若cos θ＝，θ∈，求f的值．‎ 解：(1)f＝sin＝sin＝－.‎ ‎(2)f＝sin ‎＝sin＝(sin 2θ－cos 2θ)．‎ 因为cos θ＝，θ∈，‎ 所以sin θ＝，‎ 所以sin 2θ＝2sin θcos θ＝，‎ cos 2θ＝cos2θ－sin2θ＝，‎ 所以f＝(sin 2θ－cos 2θ)‎ ‎＝×＝.‎ B级——拔高题目稳做准做 ‎1.已知sin＝，cos 2α＝，则sin α＝(　　)‎ A. B．－ C. D．－ 解析：选C　由sin＝得sin α－cos α＝.①‎ 由cos 2α＝得cos2α－sin2α＝，‎ 所以(cos α－sin α)(cos α＋sin α)＝.②‎ 由①②可得cos α＋sin α＝－.③‎ 由①③可得sin α＝.‎ ‎2.(2018·福州质检)已知m＝，若sin＝3sin 2β，则m＝(　　)‎ A. B. C. D．2‎ 解析：选D　设A＝α＋β＋γ，B＝α－β＋γ，‎ 则2(α＋γ)＝A＋B，2β＝A－B，‎ 因为sin[2(α＋γ)]＝3sin 2β，‎ 所以sin(A＋B)＝3sin(A－B)，‎ 即sin AcosB＋cos AsinB＝3(sin Acos B－cos AsinB)，即2cos Asin B＝sin AcosB，所以tan A＝2tanB，所以m＝＝2，故选D.‎ ‎3.(2017·北京高考)在平面直角坐标系xOy中，角α与角β均以Ox为始边，它们的终边关于y轴对称．若sin α＝，则cos(α－β)＝________.‎ 解析：因为角α与角β的终边关于y轴对称，‎ 所以α＋β＝2kπ＋π，k∈Z，‎ 所以cos(α－β)＝cos(2α－2kπ－π)＝－cos 2α ‎＝－(1－2sin2α)＝－＝－.‎ 答案：－ ‎4.(2018·安徽重点中学联考)若α∈，cos＝2cos 2α，则sin 2α＝________.‎ 解析：由已知得(cos α＋sin α)＝2(cos α－sin α)·(cos α＋sin α)，‎ 所以cos α＋sin α＝0或cos α－sin α＝.‎ 由cos α＋sin α＝0得tan α＝－1，‎ 因为α∈，所以tan α＞0，‎ 所以cos α＋sin α＝0不满足条件；‎ 由cos α－sin α＝两边平方得1－sin 2α＝，‎ 所以sin 2α＝.‎ 答案： ‎5．已知α∈，且sin＋cos＝.‎ ‎(1)求cos α的值；‎ ‎(2)若sin(α－β)＝－，β∈，求cos β的值．‎ 解：(1)已知sin＋cos＝，两边同时平方，得1＋2sincos＝，则sin α＝.‎ 又<α<π，所以cos α＝－＝－.‎ ‎(2)因为<α<π，<β<π，‎ 所以－<α－β<.‎ 又sin(α－β)＝－，‎ 所以cos(α－β)＝.‎ 则cos β＝cos[α－(α－β)]‎ ‎＝cos αcos(α－β)＋sin αsin(α－β)‎ ‎＝－×＋×＝－.‎ ‎6．已知coscos＝－，α∈.‎ ‎(1)求sin 2α的值；‎ ‎(2)求tan α－的值．‎ 解：(1)coscos ‎＝cossin ‎＝sin＝－，‎ 即sin＝－.‎ ‎∵α∈，∴2α＋∈，‎ ‎∴cos＝－，‎ ‎∴ sin 2α＝sin ‎＝sincos－cossin ‎＝－×－×＝.‎ ‎(2)∵α∈，∴2α∈，‎ 又由(1)知sin 2α＝，∴cos 2α＝－.‎ ‎∴tan α－＝－＝＝＝－2×＝2.‎