2018届二轮复习（理）　推理与证明、算法、复数学案（全国通用） 8页

回扣11　推理与证明、算法、复数 ‎1．复数的相关概念及运算法则 ‎(1)复数z＝a＋bi(a，b∈R)的分类 ‎①z是实数⇔b＝0；‎ ‎②z是虚数⇔b≠0；‎ ‎③z是纯虚数⇔a＝0且b≠0.‎ ‎(2)共轭复数 复数z＝a＋bi的共轭复数＝a－bi.‎ ‎(3)复数的模 复数z＝a＋bi的模|z|＝.‎ ‎(4)复数相等的充要条件 a＋bi＝c＋di⇔a＝c且b＝d(a，b，c，d∈R)．‎ 特别地，a＋bi＝0⇔a＝0且b＝0(a，b∈R)．‎ ‎(5)复数的运算法则 加减法：(a＋bi)±(c＋di)＝(a±c)＋(b±d)i；‎ 乘法：(a＋bi)(c＋di)＝(ac－bd)＋(ad＋bc)i；‎ 除法：(a＋bi)÷(c＋di)＝＋i.‎ ‎2．复数的几个常见结论 ‎(1)(1±i)2＝±2i.‎ ‎(2)＝i，＝－i.‎ ‎(3)i4n＝1，i4n＋1＝i，i4n＋2＝－1，i4n＋3＝－i，i4n＋i4n＋1＋i4n＋2＋i4n＋3＝0(n∈Z)．‎ ‎(4)ω＝－±i，且ω0＝1，ω2＝，ω3＝1,1＋ω＋ω2＝0.‎ ‎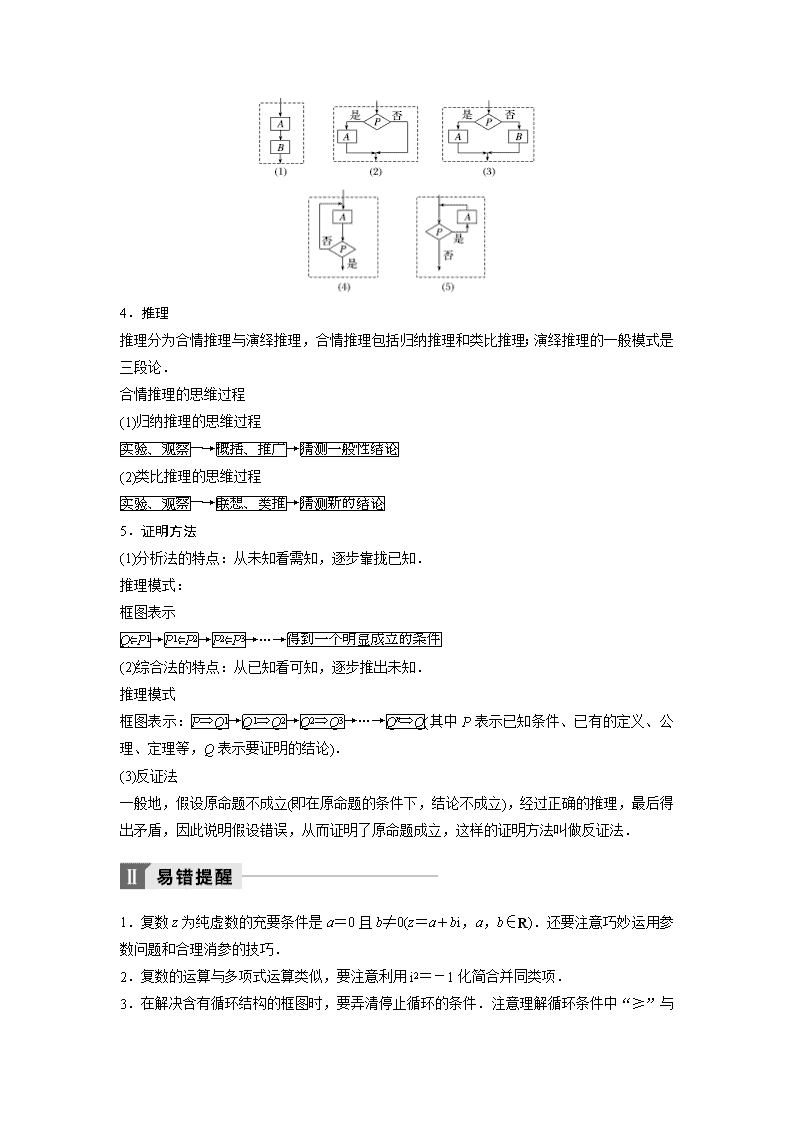3．程序框图的三种基本逻辑结构 ‎(1)顺序结构：如图(1)所示．‎ ‎(2)条件结构：如图(2)和图(3)所示．‎ ‎(3)循环结构：如图(4)和图(5)所示．‎ ‎4．推理 推理分为合情推理与演绎推理，合情推理包括归纳推理和类比推理；演绎推理的一般模式是三段论．‎ 合情推理的思维过程 ‎(1)归纳推理的思维过程 ―→→ ‎(2)类比推理的思维过程 ―→→ ‎5．证明方法 ‎(1)分析法的特点：从未知看需知，逐步靠拢已知．‎ 推理模式：‎ 框图表示 →→→…→ ‎(2)综合法的特点：从已知看可知，逐步推出未知．‎ 推理模式 框图表示：→→→…→(其中P表示已知条件、已有的定义、公理、定理等，Q表示要证明的结论)．‎ ‎(3)反证法 一般地，假设原命题不成立(即在原命题的条件下，结论不成立)，经过正确的推理，最后得出矛盾，因此说明假设错误，从而证明了原命题成立，这样的证明方法叫做反证法．‎ ‎1．复数z为纯虚数的充要条件是a＝0且b≠0(z＝a＋bi，a，b∈R)．还要注意巧妙运用参数问题和合理消参的技巧．‎ ‎2．复数的运算与多项式运算类似，要注意利用i2＝－1化简合并同类项．‎ ‎3．在解决含有循环结构的框图时，要弄清停止循环的条件．注意理解循环条件中“≥”与 ‎“＞”的区别．‎ ‎4．解决程序框图问题时，要注意流程线的指向与其上文字“是”“否”的对应．‎ ‎5．类比推理易盲目机械类比，不要被表面的假象(某一点表面相似)迷惑，应从本质上类比．用数学归纳法证明时，易盲目以为n0的起始值n0＝1，另外注意证明传递性时，必须用n＝k成立的归纳假设．‎ ‎6．在循环结构中，易错误判定循环体结束的条件，导致错求输出的结果．‎ ‎1．复数z满足z(2－i)＝1＋7i，则复数z的共轭复数为(　　)‎ A．－1－3i B．－1＋3i C．1＋3i D．1－3i 答案　A 解析　∵z(2－i)＝1＋7i，‎ ‎∴z＝＝＝＝－1＋3i，‎ 共轭复数为－1－3i.‎ ‎2．复数z1，z2在复平面内对应的点关于直线y＝x对称，且z1＝3＋2i，则z1·z2等于(　　)‎ A．13i B．－13i C．13＋12i D．12＋13i 答案　A 解析　z1＝2＋3i，z1·z2＝(2＋3i)(3＋2i)＝13i.‎ ‎3．用反证法证明命题：三角形的内角至少有一个钝角．假设正确的是(　　)‎ A．假设至少有一个钝角 B．假设至少有两个钝角 C．假设没有一个钝角 D．假设没有一个钝角或至少有两个钝角 答案　C 解析　原命题的结论为至少有一个钝角．则反证法需假设结论的反面．“至少有一个”的反面为“没有一个”，即假设没有一个钝角．‎ ‎4．下面几种推理过程是演绎推理的是(　　)‎ A．由平面三角形的性质推测空间三棱锥的性质 B．所有的金属都能够导电，铀是金属，所以铀能够导电 C．高一参加军训有12个班，1班51人，2班53人，3班52人，由此推测各班都超过50人 D．在数列{an}中，a1＝2，an＝2an－1＋1(n≥2)，由此归纳出{an}的通项公式 答案　B 解析　A．由平面三角形的性质推测空间三棱锥的性质为类比推理．‎ B．所有的金属都能够导电，铀是金属，所以铀能够导电．由一般到特殊，为演绎推理．‎ C．高一参加军训有12个班，1班51人，2班53人，3班52人，由此推测各班都超过50人为归纳推理．‎ D．在数列{an}中，a1＝2，an＝2an－1＋1(n≥2)，由此归纳出{an}的通项公式为归纳推理．‎ ‎5．z＝(m∈R，i为虚数单位)在复平面上的点不可能位于(　　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 答案　D 解析　z＝＝，‎ 由于m－1＜m＋1，故不可能在第四象限．‎ ‎6.阅读如图所示的程序框图，运行相应的程序，若输出的S为，则判断框中填写的内容可以是(　　)‎ A．n＝6 B．n＜6‎ C．n≤6 D．n≤8‎ 答案　C 解析　S＝0，n＝2，判断是，‎ S＝，n＝4，判断是，‎ S＝＋＝，n＝6，判断是，S＝＋＋＝，n＝8，判断否，输出S，故n≤6. ‎ ‎7．以下是解决数学问题的思维过程的流程图：‎ 在此流程图中，①，②两条流程线与“推理与证明”中的思维方法匹配正确的是(　　)‎ A．①—综合法，②—分析法 B．①—分析法，②—综合法 C．①—综合法，②—反证法 D．①—分析法，②—反证法 答案　A 解析　根据已知可得该结构图为证明方法的结构图．‎ 由已知到可知，进而得到结论的应为综合法，由未知到需知，进而找到与已知的关系为分析法，故①②两条流程线代表“推理与证明”中的思维方法是①—综合法，②—分析法．‎ ‎8．执行如图所示的程序框图，若输出的是n＝6，则输入整数p的最小值为(　　)‎ A．15 B．16 C．31 D．32‎ 答案　B 解析　列表分析如下：‎ ‎　　　 是否继续循环　　　S　　　n 循环前　　　　　　　　　　 0　　 1‎ 第一圈　　是　　　　　　　 1　　 2‎ 第二圈　　是　　　　　　　 3　　 3‎ 第三圈　　是　　　　　　　 7　　 4‎ 第四圈　　是　　　　　　　 15　 5‎ 第五圈　　是　　　　　　　 31　 6‎ 第六圈　　否 故当S值不大于15时继续循环，大于15但不大于31时退出循环，故p的最小正整数值为16.‎ ‎9．小明用电脑软件进行数学解题能力测试，每答完一道题，软件都会自动计算并显示出当前的正确率(正确率＝已答对题目数÷已答题目总数)，小明依次共答了10道题，设正确率依次为a1，a2，a3，…，a10.现有三种说法：①若a1＜a2＜a3＜…＜a10，则必是第一道题答错，其余题均答对；②若a1＞a2＞a3＞…＞a10，则必是第一道题答对，其余题均答错；③有可能a5＝2a10，其中正确的个数是(　　)‎ A．0 B．1 C．2 D．3‎ 答案　D 解析　①②显然成立，③前5个全答对，后5个全答错，符合题意，故选D.‎ ‎10．下列类比推理的结论不正确的是(　　)‎ ‎①类比“实数的乘法运算满足结合律”，得到猜想“向量的数量积运算满足结合律”；‎ ‎②类比“设等差数列{an}的前n项和为Sn，则S4，S8－S4，S12－S8成等差数列”， 得到猜想“设等比数列{bn}的前n项积为Tn，则T4，，成等比数列”； ‎ ‎③类比“平面内，垂直于同一条直线的两直线相互平行”，得到猜想“空间中，垂直于同一条直线的两直线相互平行”；‎ ‎④类比“设AB为圆的直径，P为圆上任意一点，直线PA，PB的斜率存在，则kPA·kPB为常数”，得到猜想“设AB为椭圆的长轴，P为椭圆上任意一点，直线PA，PB的斜率存在，则kPA·kPB为常数”. ‎ A．①④ B．①③ C．②③ D．②④‎ 答案　B 解析　②等差数列中结论成立，而等比数列中T4＝a·q6，＝a·q22，＝a·q38也成立；‎ ‎④由圆中kPA·kPB为－1，而类比到椭圆：‎ kPA·kPB＝－或－，也成立；‎ ‎①类比“实数的乘法运算满足结合律”，得到猜想“向量的数量积运算满足结合律” 不成立，即a·b·c≠a·(b·c)，这由向量数量积的定义决定的．‎ ‎③类比“平面内，垂直于同一条直线的两直线相互平行”，得到猜想“空间中，垂直于同一条直线的两直线相互平行”不成立，空间中可能出现相交，异面的情况．故选B.‎ ‎11．图中的实心点个数1,5,12,22，…，被称为五角形数，其中第1个五角形数记作a1＝1，第2个五角形数记作a2＝5，第3个五角形数记作a3＝12，第4个五角形数记作a4＝22，…，若按此规律继续下去，则an＝__________.‎ 答案　 解析　由题观察所给的图形，对应的点分别为1,1＋4,1＋4＋7,1＋4＋7＋10，…，可得点的个数为首项为1，公差为3的等差数列的和，‎ 则 an＝Sn＝n＋＝.‎ ‎12．在△ABC中，AD平分∠A的内角且与对边BC交于D点，则＝，将命题类比到空间：在三棱锥A－BCD中，平面ADE平分二面角B－AD－C且与对棱BC交于E 点，则可得到的正确命题结论为________．‎ 答案　＝ 解析　在△ABC中，作DE⊥AB，DF⊥AC，则DE＝DF，所以＝＝，根据面积类比体积，长度类比面积可得＝，即＝.‎ ‎13．执行如图所示的程序框图，则输出的结果是________．‎ 答案　32‎ 解析　由题意得log2＝log2(n＋1)－log2(n＋2)，由程序框图的计算公式，可得 S＝(log22－log23)＋(log23－log24)＋…＋[log2n－log2(n＋1)]＝1－log2(n＋1)，由S＜－4，‎ 可得1－log2(n＋1)＜－4⇒log2(n＋1)＞5，解得n＞31，‎ 所以输出的n为32.‎ ‎14．在平面上，如果用一条直线去截正方形的一个角，那么截下的一个直角三角形，按图所标边长，由勾股定理有c2＝a2＋b2.猜想正方形换成正方体，把截线换成如图的截面，这时从正方体上截下三条侧棱两两垂直的三棱锥O－LMN，如果用S1，S2，S3表示三个侧面面积，S4表示截面面积，那么类比得到的结论是________．‎ 答案　S＋S＋S＝S 解析　将侧面面积类比为直角三角形的直角边，截面面积类比为直角三角形的斜边，可得 S＋S＋S＝S.‎ ‎15．复数z＝(m2＋3m－4)＋(m2－10m＋9)i(m∈R)，‎ ‎(1)当m＝0时，求复数z的模；‎ ‎(2)当实数m为何值时，复数z为纯虚数；‎ ‎(3)当实数m为何值时，复数z在复平面内对应的点在第二象限？ ‎ 解　(1)当 m＝0时，z＝－4＋9i，‎ ‎∴＝＝.‎ ‎(2)当即 即当m＝－4时，复数z为纯虚数．‎ ‎(3)当即 ‎ 即当－4＜m＜1时， ‎ 复数z在复平面内对应的点在第二象限．‎ ‎16．(1)tan 10°tan 20°＋tan 20°tan 60°＋tan 60°tan 10°＝1；‎ ‎(2)tan 5°tan 10°＋tan 10°tan 75°＋tan 75°tan 5°＝1.‎ 由以上两式成立，推广到一般结论，写出你的推论．‎ 解　若α，β，γ都不是90°，且α＋β＋γ＝90°，则tan αtan β＋tan βtan γ＋tan αtan γ＝1.‎