山西省太原市2019-2020学年高二上学期期中考试数学试题 19页

‎2019~2020学年第一学期高二年级阶段性测评数学试卷 一、选择题：本题共12小题，每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的 ‎1.已知点，，则直线的斜率为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 由斜率的定义求解即可 ‎【详解】由斜率的定义得，‎ 故答案为：直线的斜率为 故选：‎ ‎【点睛】本题考查直线的斜率的定义，属于基础题 ‎2.在空间直角坐标系中，点与之间的距离为（ ）‎ A B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 可结合两点间距离公式求解 ‎【详解】由两点间距离公式得 故选：B ‎【点睛】本题考查空间中两点间距离公式，属于基础题 ‎3.过点且垂直于直线的直线方程为（ ）‎ A B. C. D. 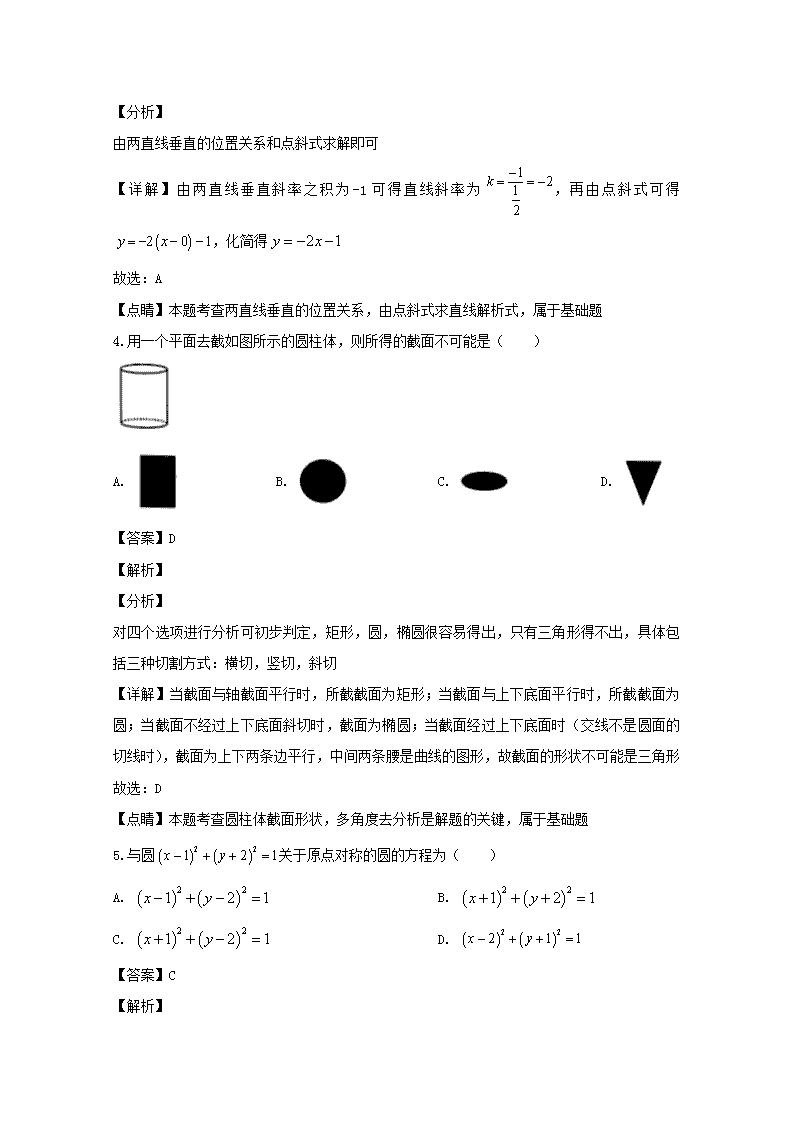‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 由两直线垂直的位置关系和点斜式求解即可 ‎【详解】由两直线垂直斜率之积为-1可得直线斜率为，再由点斜式可得，化简得 故选：A ‎【点睛】本题考查两直线垂直的位置关系，由点斜式求直线解析式，属于基础题 ‎4.用一个平面去截如图所示的圆柱体，则所得的截面不可能是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 对四个选项进行分析可初步判定，矩形，圆，椭圆很容易得出，只有三角形得不出，具体包括三种切割方式：横切，竖切，斜切 ‎【详解】当截面与轴截面平行时，所截截面为矩形；当截面与上下底面平行时，所截截面为圆；当截面不经过上下底面斜切时，截面为椭圆；当截面经过上下底面时（交线不是圆面的切线时），截面为上下两条边平行，中间两条腰是曲线的图形，故截面的形状不可能是三角形 故选：D ‎【点睛】本题考查圆柱体截面形状，多角度去分析是解题的关键，属于基础题 ‎5.与圆关于原点对称的圆的方程为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 可先求圆心关于原点的对称点，再由半径相同写出方程即可 ‎【详解】圆的圆心为，圆心关于原点的对称点为，故对称的圆的方程为：‎ 故选：C ‎【点睛】本题考查关于原点对称的点的求法，圆的标准方程的求法，属于基础题 ‎6.已知，是两条不同直线，，是两个不同的平面，则下列结论中正确的是（ ）‎ A. 若，，则 B. 若，，则 C. 若，，则 D. 若，，则 ‎【答案】B ‎【解析】‎ ‎【分析】‎ 由线面平行的性质可判断A错；由平行的递推性判断B对；C项可能性很多，与不一定垂直；D项可能性很多，不一定 ‎【详解】对A，线面平行只能推出线和过平面的交线平行，推不出和平面内的某一条线平行，如图：‎ 对B，根据平行的递推性，可得正确，如图：‎ 对C，可随机举一反例，如图：‎ 直线与斜交；‎ 对D，直线有可能相交，如图：‎ 故选：B ‎【点睛】本题考查直线与平面的位置关系，结合实例和图形较容易说明问题，属于基础题 ‎7.已知直线与直线平行，则它们之间的距离是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据两直线一般式对应系数关系求解即可 ‎【详解】由题可知，应满足，则两直线可化为，由平行直线间距离公式 故选：C ‎【点睛】本题考查两平行直线间的距离求法，属于基础题 ‎8.我国古代数学名著《九章算术》中有如下问题：“今有鳖臑下广三尺，无袤，上袤三尺，无广，高四尺.问积几何？”，鳖臑是一个四面体，每个面都是三角形，已知一个鳖臑的三视图如图粗线所示，其中小正方形网格的边长为，则该鳖臑的体积为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据三视图画出图形，结合三棱锥体积公式求解即可 ‎【详解】由三视图，画出图形，如图：‎ 则该鳖臑的体积为：‎ 故选：A ‎【点睛】本题考查由三视图求三棱锥的体积，属于基础题 ‎9.已知实数，满足条件则的最小值为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 可将目标函数转化为，再结合约束条件画出可行域，结合位置关系判断即可 ‎【详解】根据约束条件画出可行域，目标函数可转化为，要使取到最小值，则截距取到最大值，由图可知，相交于右上方的点时，有最值，即点为，代入得 故选：C ‎【点睛】本题考查根据线性约束条件求最值，正确画出图形，学会转化目标函数是解题的关键，属于基础题 ‎10.已知正方体中，，分别为，的中点，则异面直线与所成角的大小为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据题意画出图形，可将异面直线转化共面的相交直线，再进行求解 ‎【详解】如图：‎ 作的中点，连接，由题设可知，则异面直线与所成角为或其补角，设正方体的边长为4，由几何关系可得， ，，，得，即 故选：D ‎【点睛】本题考查异面直线的求法，属于基础题 ‎11.已知，，点为圆上任意一点，则面积的最大值为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 可根据题意画出图形，求三角形面积的最值可转化为求圆上一点到直线距离的最大值，由点到直线距离公式即可求解 ‎【详解】如图所示：‎ 要求三角形面积的最大值，需先求圆上一点到直线距离的最大值，求圆心到直线距离，再加上半径即可，圆可转化为，圆心为，，则直线方程为，圆心到直线的距离，则，，则 故选：C ‎【点睛】本题考查点到直线距离公式，两点间距离公式，数形结合的思想，属于中档题 ‎12.将边长为2的正沿着高折起，使，若折起后四点都在球的表面上，则球的表面积为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 通过底面三角形BCD求出底面圆的半径DM，判断球心到底面圆的距离OM，求出球O的半径，即可求解球O的表面积．‎ ‎【详解】△BCD中，BD=1，CD=1，∠BDC=120°，‎ 底面三角形的底面外接圆圆心为M，半径为：r,由余弦定理得到BC=，再由正弦定理得到 ‎ 见图示：‎ AD是球的弦，DA=，将底面的圆心M平行于AD竖直向上提起，提起到AD的高度的一半，即为球心的位置O，∴OM=，在直角三角形OMD中，应用勾股定理得到OD，OD即为球的半径.∴球的半径OD=．‎ 该球的表面积为：4π×OD2=7π；‎ 故选：B．‎ ‎【点睛】涉及球与棱柱、棱锥的切、接问题时，一般过球心及多面体中的特殊点(一般为接、切点)‎ 或线作截面，把空间问题转化为平面问题，再利用平面几何知识寻找几何体中元素间的关系，或只画内切、外接的几何体的直观图，确定球心的位置，弄清球的半径(直径)与该几何体已知量的关系，列方程(组)求解.‎ 二、填空题（共4个小题，每题4分，共16分）‎ ‎13.圆的半径为______________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 将一般式化为标准式即可求得 ‎【详解】由，则半径为 故答案为：‎ ‎【点睛】本题考查圆的一般式和标准式的互化，熟练运用配方法是解题关键，属于基础题 ‎14.已知一个圆锥的侧面展开图是一个半径为，圆心角为的扇形，则此圆锥的体积为 ．‎ ‎【答案】‎ ‎【解析】‎ 试题分析：由，得，即，∴．‎ 考点：圆锥的侧面图与体积．‎ ‎15.已知长为的线段的两个端点和分别在轴和轴上滑动，则线段的中点的轨迹方程为____________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 可采用数形结合思想进行转化，结合直角三角形斜边上的中线性质即可求得 ‎【详解】如图：‎ 不论直线怎么移动，线段的中点的始终为斜边上的中线，即，即 故答案为：‎ ‎【点睛】本题考查圆的轨迹方程的求法，数形结合的转化思想，属于基础题 ‎16.如图，在棱长为的正方体中，点分别是棱的中点,是侧面内一点，若平行于平面,则线段长度的取值范围是_________.‎ ‎【答案】‎ ‎【解析】‎ ‎【详解】试题分析：如下图所示，分别取棱中点，连接，连接，因为为所在棱的中点，所以，所以，又平面平面，所以平面；因为，所以四边形为平行四边形，所以，又平面，平面，所以平面，又，所以平面，因为是侧面内一点，且平面，则必在线段上，在直角中，，同理，在直角中，求得，所以为等腰三角形，当在中点时，，此时最短，位于 处时最长，，，所以线段长度的取值范围是.‎ 考点：点、线、面的距离问题.‎ ‎【方法点晴】本题主要考查了点、线、面的距离问题，其中解答中涉及到直线与平面平行的判定与性质，三角形的判定以及直角三角形的勾股定理等知识点的综合考查，着重考查了学生分析问题和解答问题的能力，以及推理与运算能力，同时考查了学生空间想象能力的训练，试题有一定的难度，属于中档试题.‎ 三、解答题（共5个小题，共48分）‎ ‎17.已知的顶点，，是的中点.‎ ‎（1）求直线的方程；‎ ‎（2）求边上的高所在直线的方程.‎ ‎【答案】（1）；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）先设，再结合中点坐标公式求解即可；‎ ‎（2）所求直线与直线垂直，可算出斜率，又直线过点，利用点斜式即可求解；‎ ‎【详解】（1）设，由题意得∴∴. ‎ ‎∴直线的方程为； ‎ ‎（2）∵，，∴，‎ ‎∴边上的高所在直线的斜率， ‎ ‎∴边上高所在直线方程为：，即.‎ ‎【点睛】本题考查中点坐标公式，直线方程的求法，属于基础题 ‎18.如图，在正方体中，，分别是，的中点.‎ ‎（1）求证：平面；‎ ‎（2）求证：平面.‎ ‎【答案】（1）证明见解析；（2）证明见解析.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）要证直线平面，可在平面中找一条线与平行，连接，先证明是平行四边形，再根据线面平行的判定定理即可求证；‎ ‎（2）结合线面垂直的判定定理，证明直线平面的两条交线即可；‎ ‎【详解】（1）连接，∵是正方体，，，‎ ‎∵，分别是，的中点，∴，.‎ ‎∴是平行四边形，∴，‎ ‎∵平面，平面，‎ ‎∴平面； ‎ ‎（2）由（1）得，∵是正方体.‎ ‎∴平面，∴，∴，‎ ‎∵是正方体，∴是正方体，‎ ‎∴，∴，‎ ‎∵平面，平面，，‎ ‎∴平面.‎ ‎【点睛】本题考查线面平行，线面垂直的证明，属于基础题 ‎19.已知圆与圆.‎ ‎（1）若圆与圆外切，求实数的值；‎ ‎（2）在（1）的条件下，若直线与圆的相交弦长为，求实数的值.‎ ‎【答案】（1）5；（2）或.‎ ‎【解析】‎ 分析】‎ ‎（1）先将圆化成标准式，利用两圆相切的性质，得圆心距等于半径之和，即，即可求解；‎ ‎（2）结合圆的几何性质，圆的半径，弦心距，半弦长构成直角三角形，可将弦长问题转化成圆心到直线距离问题，可进一步求解 ‎【详解】（1）∵，∴，，‎ ‎∵，∴，∴，， ‎ ‎∵圆与圆外切，∴，∴，∴； ‎ ‎（2）由（1）得，圆的方程为，，，‎ 由题意可得圆心到直线的距离， ‎ ‎∴或.‎ ‎【点睛】本题考查两圆相切的几何性质，直线与圆的位置关系，属于基础题 ‎20.如图，在四棱锥中，，,,,是正三角形.‎ ‎（1）求证：；‎ ‎（2）求与平面所成角的正弦值.‎ ‎【答案】（1）证明见解析；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据线面垂直的判定定理，可利用已知条件，先证直线平面，又平面，即可得证；‎ ‎（2）作点的中点，连接，，由面面垂直的和判定定理可得与平面所成角为，通过计算即可求得 ‎【详解】（1）证明：∵是正三角形，，‎ ‎∴，，∴，∴，‎ ‎∵，平面，∴； ‎ ‎（2）设点是的中点，连接，，‎ ‎∵是正三角形，∴，，‎ 由（1）得平面，∴平面平面，‎ ‎∴平面，‎ ‎∴与平面所成角为， ‎ ‎∵，∴,‎ ‎∴.‎ ‎【点睛】本题考查线线垂直的证明，求线面角的夹角的正弦值，属于中档题 ‎21.如图，在四棱锥中，，，,，是正三角形.‎ ‎（1）求证：；‎ ‎（2）求二面角的大小.‎ ‎【答案】（1）证明见解析；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）通过线面垂直来证线线垂直，先证平面，再说明平面，即可得证；‎ ‎（2）设点是的中点，连接，，通过几何关系可得是二面角的平面角，再计算即可 ‎【详解】（1）证明：∵是正三角形，，‎ ‎∴，，∴，∴，‎ ‎∵，平面，∴；‎ ‎（2）设点是的中点，连接，，‎ ‎∵是正三角形，∴，，‎ ‎∵，∴，‎ ‎∵，∴，‎ ‎∵，，∴是正方形，‎ ‎∴，∴平面，∴，‎ ‎∴是二面角的平面角， ‎ 由（1）得平面，∴，∴，‎ ‎∴，∴.‎ ‎【点睛】本题考查线面平行的证明，二面角大小的求法，属于中档题 ‎22.已知圆，点是直线上的动点，过点作圆的切线，，切点分别为，.‎ ‎（1）当时，求点的坐标；‎ ‎（2）当取最大值时，求的外接圆方程.‎ ‎【答案】（1）或；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由题知，可设，切线长，半径，圆心与点的长度组成直角三角形，故有，结合两点间距离公式和直线方程，可求得点的坐标；‎ ‎（2）当圆心到直线距离最短时，可确定点位置，此时圆心位置为点与点的中点坐标，半径为，结合垂直关系和直线方程可求点，进而求得的外接圆方程 ‎【详解】（1）设，∵，∴，，‎ ‎∵，∴， ‎ ‎∴解得或 ‎ ‎∴或； ‎ ‎（2）由题意可知当时，取最大值，设此时，‎ 由得∴， 的外接圆圆心为，半径，∴的外接圆方程为.‎ ‎【点睛】本题考查直线与圆的位置关系，两点间距离公式的应用，圆的几何性质，勾股定理的应用，图形与方程的转化思想，属于中档题 ‎23.已知圆，点是直线上的动点，过点作圆的切线，，切点分别为，.‎ ‎（1）当时，求点的坐标；‎ ‎（2）设的外接圆为圆，当点在直线上运动时，圆是否过定点（异于原点）？若过定点，求出该定点的坐标；若不过定点，请说明理由.‎ ‎【答案】（1）或；（2）是过定点，.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由题知，可设，切线长，半径，圆心与点的长度 组成直角三角形，故有，结合两点间距离公式和直线方程，可求得点的坐标；‎ ‎（2）可先设，则，整理得的外接圆方程为，结合代换得，要使圆恒过定点满足，即，解出对应的，即可求解 ‎【详解】（1）设，∵，∴，，‎ ‎∵，∴， ‎ ‎∴解得或 ‎ ‎∴或； ‎ ‎（2）设，则，‎ ‎∴的外接圆方程为， ‎ ‎∵，∴，‎ ‎∴，令 则或（舍去），∴圆过定点.‎ ‎【点睛】本题考查直线与圆的位置关系，两点间距离公式的应用，求证轨迹恒过定点问题，解题关键在于正确表示出外切圆方程，学会利用直线上的点满足的方程进行代换，将方程转化成恒成立问题，属于中档题 ‎ ‎