【数学】2018届一轮复习人教A版一元二次不等式及其解法教案 8页

高三 一轮复习 6.2 一元二次不等式及其解法 【教学目标】 1.会从实际问题的情境中抽象出一元二次不等式模型． 2.通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系． 3.会解一元二次不等式，对给定的一元二次不等式，会设计求解的程序框图. 【重点难点】 1.教学重点会解一元二次不等式并了解一元二次不等式与相应的二次函数、一元二次方程 的联系； 2.教学难点学会对知识进行整理达到系统化，提高分析问题和解决问题的能力； 【教学策略与方法】 自主学习、小组讨论法、师生互动法 【教学过程】 教学流程 教师活动 学生活动 设计意图 考纲传真 1.会从实际问题的情境中抽象出一元二次不等式模 型．2.通过函数图象了解一元二次不等式与相应的二 次函数、一元二次方程的联系．3.会解一元二次不等 式，对给定的一元二次不等式，会设计求解的程序框 图. 真题再现; 1．(2014·浙江 6)已知函数 f(x)＝x 3＋ax2＋bx＋c，且 09 解析　由题意，不妨设 g(x)＝x 3＋ax2＋bx＋c－m， m∈(0，3]，则 g(x)的三个零点分别为 x1＝－3，x2＝－ 2，x3＝－1，因此有(x＋1)(x＋2)(x＋3)＝x3＋ax2＋bx＋ c－m，则 c－m＝6，因此 c＝m＋6∈(6，9]． 答案　C 2．(2012·重庆，2)不等式 x－1 2x＋1≤0 的解集为(　　) A.(－1 2，1] B.[－1 2，1] C.(－∞，－1 2)∪[1，＋∞) 。 学生通过对高 考真题的解决，发 现自己对知识的 掌握情况。 通 过 对 考 纲 的解读和分析。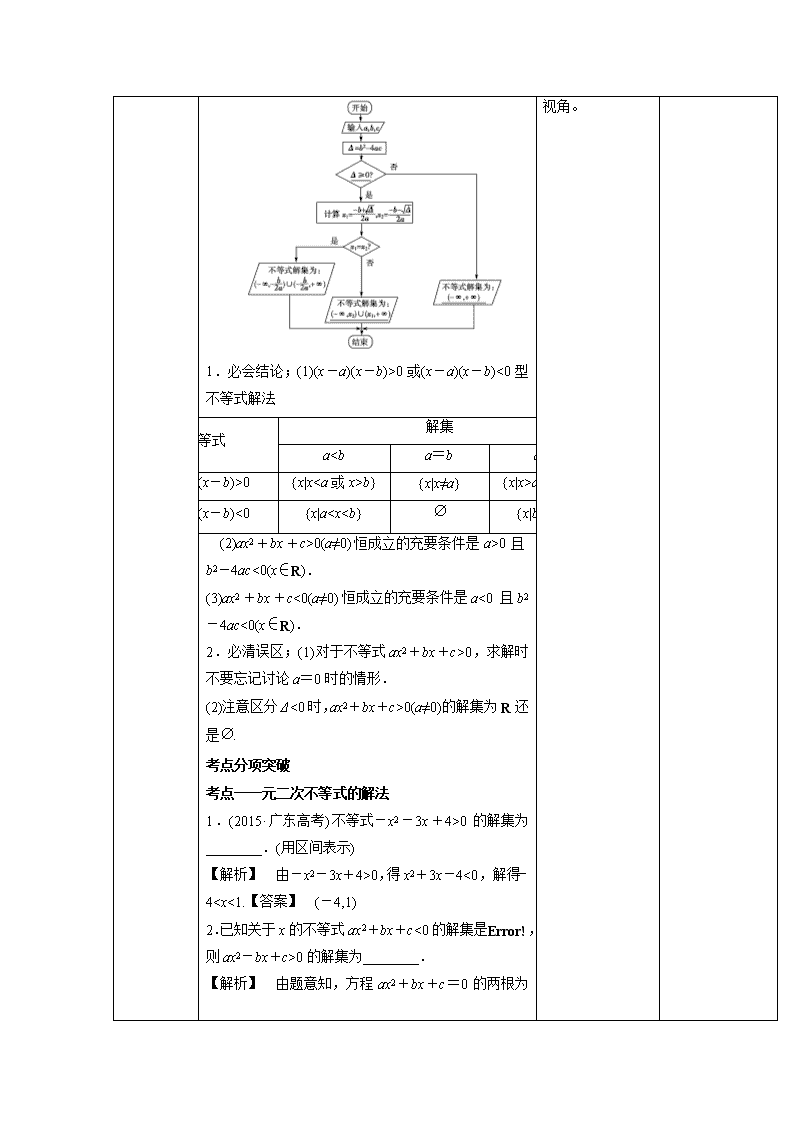 让学生明确考试 要求，做到有的 放矢 D.(－∞，－1 2]∪[1，＋∞) 解析　不等式可化为{（x－1）（2x＋1） ≤ 0， 2x＋1 ≠ 0， 解不 等式组得－1 20 Δ＝0 Δ<0 二次函数 y＝ax2 ＋bx＋c (a>0)的 图象 一元二次方程 ax2＋bx＋c＝ 0(a>0)的根 有两相异实根 x1，x2(x10 (a>0)的解集 {x|xx2} {x|x≠x1} R ax2＋bx＋c<0 (a>0)的解集 {x|x10 或(x－a)(x－b)<0 型 不等式解法 解集 不等式 ab (x－a)(x－b)>0 {x|xb} {x|x≠a} {x|x>a 或 x0(a≠0)恒成立的充要条件是 a>0 且 b2－4ac<0(x∈R)． (3)ax2 ＋bx＋c<0(a≠0)恒成立的充要条件是 a<0 且 b 2 －4ac<0(x∈R)． 2．必清误区；(1)对于不等式 ax 2＋bx＋c>0，求解时 不要忘记讨论 a＝0 时的情形． (2)注意区分 Δ<0 时，ax2＋bx＋c>0(a≠0)的解集为 R 还 是∅. 考点分项突破 考点一一元二次不等式的解法 1．(2015·广东高考)不等式－x 2 －3x＋4>0 的解集为 ________．(用区间表示) 【解析】　由－x2－3x＋4>0，得 x2＋3x－4<0，解得－ 40 的解集为________． 【解析】　由题意知，方程 ax2＋bx＋c＝0 的两根为 视角。 环节二 －2 和－1 2，且 a<0，所以－b a＝－5 2，c a＝1.不等式 ax2－bx＋ c>0 可转化为 x2－b ax＋c a<0，即 x2－5 2x＋1<0，即 2x2－ 5x＋2<0.解得1 21.当 a<0 时，原不等式可化为(ax－1)(x－1)<0，即 (x－1 a )(x－1)>0.∵1 a<1，∴x>1 或 x<1 a. 当 a>0 时，原不等式可化为(x－1 a )(x－1)<0， ①若 01，∴11，则1 a<1，∴1 a1}； 当 01 时，不等式的解集为Error!. 归纳解含参数的一元二次不等式的步骤 1．二次项系数若含有参数应讨论是等于 0，小于 0， 还是大于 0，然后将不等式转化为二次项系数为正的 形式． 2．判断方程的根的个数，讨论判别式 Δ 与 0 的关系． 3．确定无根时可直接写出解集，确定方程有两个根时， 要讨论两根的大小关系，从而确定解集形式． 考点二 一元二次不等式恒成立问题 (1)如果不等式(m＋1)x2＋2mx＋m＋1>0 对任意实数 x 都成立，则实数 m 的取值范围是(　　) A．m>－1 B．－1－1 2 D．m<－1 或 m>－1 2 (2)若不等式 x2＋ax＋1≥0 对一切 x∈(0，1 2 ]成立，求 a 的最小值． 【解析】　(1)当 m＋1＝0 时，不等式可化为－2x>0， 不满足题意．当 m＋1≠0 时，由题意可得Error!解得 m>－1 2. 【答案】　C (2)设 f(x)＝x2＋ax＋1，则对称轴为 x＝－a 2， 若－a 2≥1 2，即 a≤－1 时，则 f(x)在 (0，1 2 )上是减函数． 应有 f(1 2 )≥0⇒－5 2≤a≤－1，若－a 2≤0，即 a≥0 时，f(x) 在(0，1 2 )上是增函数，应有 f(0) ＝1>0 恒成立，故 a≥0. 若 0≤－a 2≤1 2，即－1≤a≤0.则应有 f(－a 2 )＝a2 4 －a2 2 ＋1＝1 －a2 4 ≥0 恒成立．故－1≤a≤0. 综上 a≥－5 2，即 a 的最小值为－5 2. 跟踪训练 1.设函数 f(x)＝mx 2－mx－1(m≠0)，若对于 x∈[1,3]，f(x)<－m＋5 恒成立，求 m 的取值范围． 【解】　要使 f(x)<－m＋5 在[1,3]上恒成立． 则 mx2－mx＋m－6<0，即 m(x－1 2 )2＋3 4m－6<0 在 x∈[1,3] 上恒成立，令 g(x) ＝m(x－1 2 )2 ＋3 4m －6 ， x∈[1,3]．当 m>0 时，g(x)在[1,3]上是增函数， 所以 g(x)max＝g(3)＝7m－6<0.所以 m<6 7，则 00，解得 x<－3 或 x>1 2. [错解分析]　指出上述解法的错误并指出错误原因． 提示忽视二次项系数的符号．原因是对一元二次不等 式的解法掌握不牢固． [自我纠正]　由题意知，－1 3，2 是方程 ax2＋bx＋c＝ 0(a≠0)的两根，由根与系数的关系知Error!所以 b＝－5 3 a，c＝－2 3a. 所以不等式 cx2＋bx＋a<0 可化为－2 3ax2－5 3ax＋a<0. 由题意知 a<0，∴原不等式等价于 2 3x2＋5 3x－1<0， 解得－3