2018届二轮复习传统文化与高考数学课件（全国通用） 39页

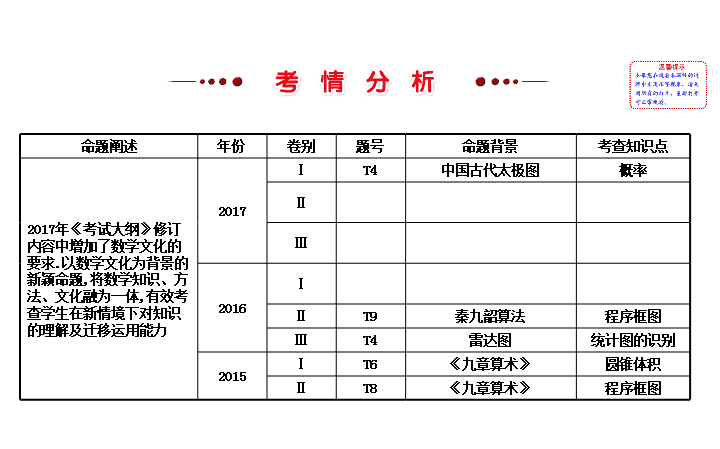
特色专题　 传统文化与高考数学 命题阐述 年份 卷别 题号 命题背景 考查知识点 2017 年 《 考试大纲 》 修订内容中增加了数学文化的要求 . 以数学文化为背景的新颖命题 , 将数学知识、方法、文化融为一体 , 有效考查学生在新情境下对知识的理解及迁移运用能力 2017 Ⅰ T4 中国古代太极图 概率 Ⅱ Ⅲ 2016 Ⅰ Ⅱ T9 秦九韶算法 程序框图 Ⅲ T4 雷达图 统计图的识别 2015 Ⅰ T6 《 九章算术 》 圆锥体积 Ⅱ T8 《 九章算术 》 程序框图 命题背景一　渗透数学美的考查 【 典例 】 (1)(2017· 全国卷 Ⅰ) 如图 , 正方形 ABCD 内的图形来自中国古代的太极图 . 正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称 . 在正方形内随机取一点 , 则此点取自黑色部分的概率是　 ( 　　 ) (2)(2017· 郑州二模 ) 我国古代数学名著 《 九章算 术 》 中割圆术有 :“ 割之弥细 , 所失弥少 , 割之又割 , 以 至于不可割 , 则与圆周合体而无所失矣 .” 其体现的是 一种无限与有限的转化过程 , 比如在 中“ …” 即代表无限次重复 , 但原式却是个定值 x, 这 可以通过方程 =x 确定 x=2, 则 =________. 　世纪金榜导学号 92494144 【 解题导引 】 (1) 先分别求出正方形和黑色部分面积 , 再利用几何概型的概率公式求解 . (2) 令 =x, 得出关于 x 的一元二次方程 , 即可 求解 . 【 解析 】 (1) 选 B. 设正方形边长为 2, 则圆半径为 1, 则 正方形的面积为 2×2=4, 圆的面积为 π×1 2 =π, 图中 黑色部分的面积为 , 则此点取自黑色部分的概率为 (2) 由题意 , 可令 =x, 即 1+ =x, 即 x 2 -x-1=0, 解得 答案 : 【 赏析感悟 】 数学文化的美学特征是构成数学文化的重要内容 . 数学美表现为一种抽象、严谨、含蓄的理性美 , 从表现形式上分为数学内容的和谐美、数学结构的形式美、几何图形的构造美、数学公式的简洁美 . 纵观数学领域的一切公式、公理和定理 , 无不是对客观世界存在的秩序、对称、和谐、统一的美的反映 . 【 好题链接 (1+1)】 1.(2017· 泰安二模 ) 鲁班锁是中国传 统的智力玩具 , 起源于古代汉族建筑 中首创的榫卯结构 , 这种三维的拼插 器具内部的凹凸部分 ( 即榫卯结构 ) 啮合 , 十分巧妙 , 外 观看是严丝合缝的十字立方体 , 其上下、左右、前后 完全对称 . 从外表上看 , 六根等长的正四棱柱体分成三组 , 经 90° 榫卯起来 , 如图 , 若正四棱柱体的高为 6, 底面正方形的边长为 1, 现将该鲁班锁放进一个球形容器内 , 则该球形容器的表面积的最小值为 ________.( 容器壁的厚度忽略不计 ) 【 解析 】 表面积最小的球形容器可以看成长、宽、高 分别为 1 、 2 、 6 的长方体的外接球 . 设其半径为 R, (2R) 2 =6 2 +2 2 +1 2 , 解得 R 2 = , 所以该球形容器的表面 积的最小值为 4πR 2 =41π. 答案 : 41π 2.( 新题预测 ) 我国古代 ,9 是数字之极 , 代 表尊贵之意 , 所以中国古代皇家建筑中包 含许多与 9 相关的设计 . 例如 , 北京天坛圆 丘的底面由扇环形的石板铺成 ( 如图 ), 最高一层是一块天心石 , 围绕它的第一圈有 9 块石板 , 从第二圈开始 , 每一圈比前一圈多 9 块 , 共有 9 圈 , 则前 9 圈的石板总数是 ________. 【 解析 】 前 9 圈的石板数依次组成一个首项为 9, 公差 为 9 的等差数列 ,S 9 =9×9+ ×9=405. 答案 : 405 命题背景二　渗透古代名家 ( 学派 ) 研究数学的考查 【 典例 】 (1)(2017· 枣庄二模 ) 两千多年前 , 古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题 . 他们在沙滩上画点或用小石子表示数 , 按照点或小石子能排列的形状对数进行分类 . 如图中实心点的个数 5,9,14,20, … 为梯形数 . 根据图形的构成 , 记此数列的第 2017 项为 a 2017 , 则 a 2017 -5= 　 ( 　　 ) A.2 023×2 017 B.2 023×2 016 C.1 008×2 023 D.2017×1008 (2)(2017· 浙江高考 ) 我国古代数学家刘徽创立的“割圆术”可以估算圆周率 π, 理论上能把 π 的值计算到任意精度 . 祖冲之继承并发展了“割圆术” , 将 π 的值精确到小数点后七位 , 其结果领先世界一千多年 ,“ 割圆术”的第一步是计算单位圆内接正六边形的面积 S 内 ,S 内 =____________. 世纪金榜导学号 92494145 【 解题导引 】 (1) 观察梯形数的前几项 , 归纳得 a n =2+3+ … +(n+2), 结合等差数列的前 n 项和求得 a n , 然后求 a 2017 -5 即可得出结论 . (2) 根据圆内接正六边形的边长与半径的关系求单位圆内接正六边形的面积 . 【 解析 】 (1) 选 C. 观察梯形数的前几项 , 得 5=2+3=a 1 , 9=2+3+4=a 2 , 14=2+3+4+5=a 3 , … a n =2+3+ … +(n+2)= 由此可得 a 2017 = ×2018×2021=1009×2021. a 2017 -5=(1008+1)(2023-2)-5=1008×2023. (2) 如图 , 因为是单位圆 , 所以 OA=1, 因 为六边形 ABCDEF 是正六边形 , 所以 △ OAB 是正三角形 , 所以 AB=1, 过点 O 作 OG⊥AB 于点 G, 所以 OG=OAsin60°= , 所以正六边 形的面积为 6S △OAB =6× ×AB · OG= . 答案 : 【 赏析感悟 】 本例 (1) 以古希腊毕达哥拉斯学派的研究故事为背景 ,(2) 以我国古代数学家刘徽创立的“割圆术”为命题背景 , 分别考查了数列问题和圆内接正六边形面积问题 . 其中毕达哥拉斯学派的“形数”问题 , 备受命题者的青睐 , 已成为高考命题的热点问题 . 【 好题链接 (1+1)】 1.(2017· 聊城二模 ) 远古时期 , 人们通过在 绳子上打结来记录数量 , 即“结绳计数” . 如图所示的是一位母亲记录的孩子自出生 后的天数 , 在从右向左依次排列的不同绳子上打结 , 满 七进一 , 根据图示可知 , 孩子已经出生的天数是 ( 　　 ) A.336 　　　 B.510 　　　 C.1 326 　　　 D.3 603 【 解析 】 选 B. 由题意满七进一 , 可得该图示为七进制数 , 化为十进制数为 1×7 3 +3×7 2 +2×7+6=510. 2.( 新题预测 ) 欧拉公式 e ix =cosx+isinx(i 为虚数单位 ) 是由瑞士著名数学家欧拉发明的 , 它将指数函数的定义域扩大到复数 , 建立了三角函数和指数函数的关系 , 它在复变函数论里占有非常重要的地位 , 被誉为“数学中的天桥” , 根据欧拉公式可知 ,e 2i 表示的复数在复平面中位于　 ( 　　 ) 世纪金榜导学号 92494146 A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 【 解析 】 选 B. 由 e ix =cosx+isinx, 可知 e 2i =cos2+isin2, 因为 2∈ , 所以 cos2∈ ,sin2∈ , 所以 e 2i 表示的复数在复平面中位于第二象限 . 命题背景三　渗透古代数学名著的考查 【 典例 】 (1)(2017· 全国卷 Ⅱ) 我国古代数学名著 《 算法统宗 》 中有如下问题 :“ 远望巍巍塔七层 , 红光 点点倍加增 , 共灯三百八十一 , 请问尖头几盏灯 ?” 意 思是 : 一座 7 层塔共挂了 381 盏灯 , 且相邻两层中的下一 层灯数是上一层灯数的 2 倍 , 则塔的顶层共有灯 ( 　　 ) A.1 盏 B.3 盏 C.5 盏 D.9 盏 (2)(2016· 四川高考 ) 秦九韶是我国南宋时期的数学家 , 普州 ( 现四川省安岳县 ) 人 , 他在所著的 《 数书九章 》 中提出的多项式求值的秦九韶算法 , 至今仍是比较先进的算法 . 如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例 . 若输入 n,x 的值分别为 3,2, 则输出 v 的值为　 ( 　　 ) 世纪金榜导学号 92494147 A.9 B.18 C.20 D.35 【 解题导引 】 (1) 由题意可知等比数列的前 7 项和为 381, 公比为 2, 根据等比数列前 n 项和公式即可求解 . (2) 根据已知的程序框图可得 , 该程序的功能是利用循环结构计算并输出变量 v 的值 , 模拟程序的运行过程 , 可得答案 . 【 解析 】 (1) 选 B. 塔的顶层共有灯 x 盏 , 则各层的灯数构 成一个公比为 2 的等比数列 , 由 =381 可得 x=3. (2) 选 B. 由程序框图知 , 初始值 :n=3,x=2,v=1,i=2, 第一次循环 :v=4,i=1; 第二次循环 :v=9,i=0; 第三次循环 :v=18,i=-1. 结束循环 , 输出当前 v 的值 18. 【 赏析感悟 】 中国古代数学取得了极其辉煌的成就 , 出现了刘徽、祖冲之等伟大的数学家 , 以及 《 九章算 术 》 等经典的数学传世之作 , 这些中国古代数学名著 是我们的丰富宝库 , 继新课程改革以来 , 高考题中出现 了一些以古代名著为命题背景的试题 , 涉及的有 《 九 章算术 》 、 《 数书九章 》 、 《 算法统宗 》 等 . 本例 分别以 《 算法统宗 》 、 《 数书九章 》 为背景 , 相应考查了数列和算法等数学知识 . 从某种意义上讲 , 这些试题的价值实际上已远远超出了试题本身 . 【 好题链接 (1+1)】 1.(2017· 正定二模 )《 九章算术 》 是我国古代数学名 著 , 它在几何学中的研究比西方早一千多年 . 例如堑堵指 底面为直角三角形 , 且侧棱垂直于底面的三棱柱 ; 阳马指 底面为矩形 , 一侧棱垂直于底面的四棱锥 . 如图 , 在堑堵 ABC-A 1 B 1 C 1 中 ,AC⊥BC, 若 A 1 A=AB=2, 当阳马 B-A 1 ACC 1 体积 最大时 , 则堑堵 ABC-A 1 B 1 C 1 的体积为　 ( 　　 ) 世纪金榜导学号 92494148 【 解析 】 选 C. 由阳马的定义知 ×A 1 A×AC× BC= AC×BC≤ (AC 2 +BC 2 )= AB 2 = , 当且仅当 AC=BC= 时等号成立 , 所以当阳马 B-A 1 ACC 1 体积最大 时 , 则堑堵 ABC-A 1 B 1 C 1 的体积为 2.( 新题预测 ) 中国古代数学著作 《 算法统综 》 中有这样一个问题 :“ 三百七十八里关 , 初步健步不为难 , 次日脚痛减一半 , 六朝才得到其关 , 要见次日行里数 , 请公仔细算相还” . 其大意为 :“ 有一个人走 378 里路 , 第一天健步行走 , 从第二天起脚痛每天走的路程为前一天的一半 , 走了 6 天后到达目的地” . 则该人第五天走的路程为　 ( 　　 ) A.48 里 B.24 里 C.12 里 D.6 里 【 解析 】 选 C. 设第一天的路程为 a 1 里 , 则 =378,a 1 =192, 所以 a 5 =a 1 × =192× =12.