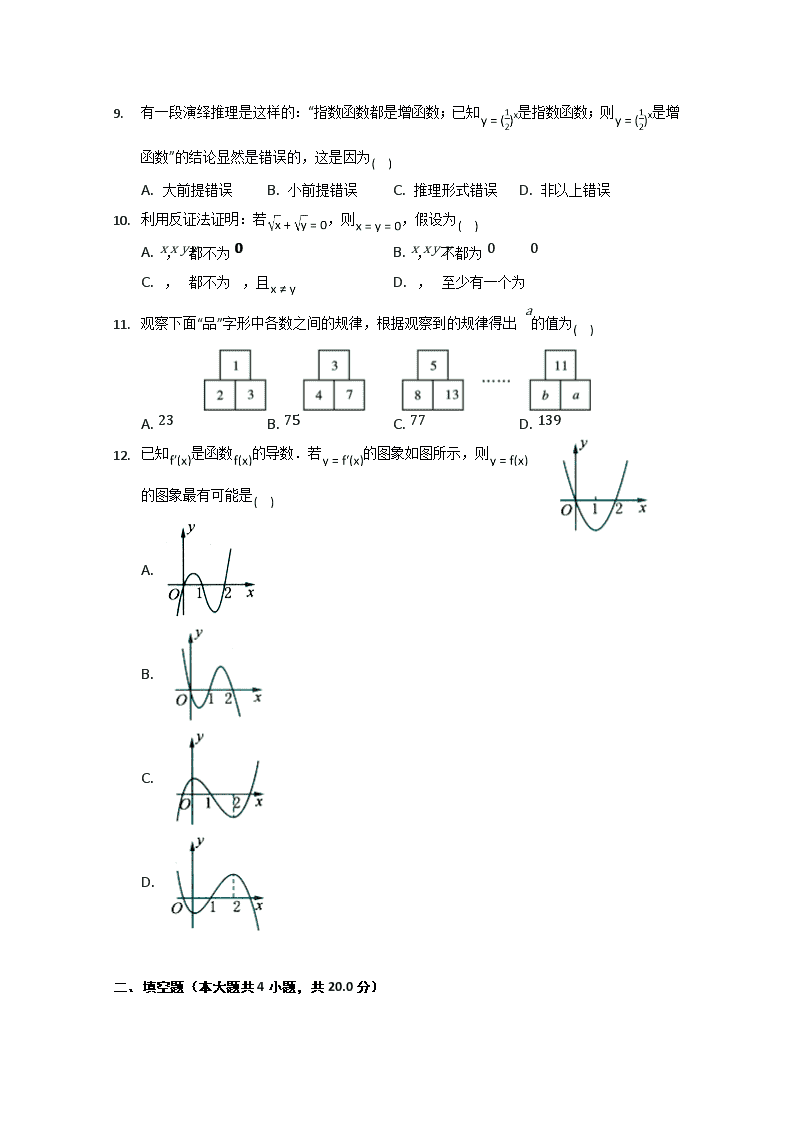安徽省凤阳县第二中学2019-2020学年高二4月月考数学（理）试题 8页

凤阳县第二中学2019~2020学年第二学期第一次月考 高二年级 数学（理）‎ 一、选择题（本大题共12小题，共60.0分）‎ 1. 设i为虚数单位，则复数 A. 0 B. ‎2 ‎C. 2i D. ‎ 2. 函数在处的导数的几何意义是 A. 在点处的斜率 B. 曲线在点处切线的斜率 C. 在点处的切线与x轴所夹锐角的正切值 D. 点与点连线的斜率 3. 若物体的运动方程是，时物体的瞬时速度是 A. 33 B. ‎31 ‎C. 39 D. 27‎ 4. 设复数Z满足，则 A. B. C. D. 2‎ 5. 设，若，则a的值等于 A. B. C. D. ‎ 6. 曲线在点处的切线方程为    ‎ A. B. C. D. ‎ 7. 函数的最大值是 A. 1 B. C. 0 D. ‎ 8. 曲线与直线所围成的封闭图象的面积是    ‎ A. B. C. D. ‎ 1. 有一段演绎推理是这样的：“指数函数都是增函数；已知是指数函数；则是增函数”的结论显然是错误的，这是因为 A. 大前提错误 B. 小前提错误 C. 推理形式错误 D. 非以上错误 2. 利用反证法证明：若，则，假设为 A. x，y都不为0 B. x，y不都为‎0 ‎C. x，y都不为0，且 D. x，y至少有一个为0‎ 3. 观察下面“品”字形中各数之间的规律，根据观察到的规律得出a的值为 A. 23 B. ‎75 ‎C. 77 D. 139‎ 4. 已知是函数的导数．若的图象如图所示，则的图象最有可能是 A. B. C. D. ‎ 二、填空题（本大题共4小题，共20.0分）‎ 1. 已知，则______．‎ 2. 定积分______．‎ 3. 甲、乙、丙三位同学中有一人申请了北京大学的自主招生考试，当他们被问到谁申请了北京大学的自主招生考试时，甲说：丙没有申请；乙说：甲申请了；丙说：甲说对了．如果这三位同学中只有一人说的是假话，那么申请了北京大学的自主招生考试的同学是______．‎ 4. 复数的实部为______．‎ 三、解答题（本大题共6小题，共70.0分）‎ 5. ‎(10分) 计算下列式子： ； ； ‎ 6. ‎（10分）已知函数，当自变量x由1变到时，求：‎ ‎    函数的增量．‎ ‎    函数的平均变化率．‎ ‎ ‎ 1. ‎（10分）求下列函数的导数：‎ ‎；‎ ‎． ‎ 2. ‎（12分）已知函数的图象在点处的切线方程为．‎ 求实数a，b的值；‎ 求函数的单调区间；‎ 求函数的极值． ‎ 3. ‎（14分）已知数列满足，2，3，， 求，，，； ‎ 归纳猜想通项公式． ‎ 1. ‎（14分）证明以下结论：‎ 用分析法证明．‎ 利用导数和三段论证明：函数在上是增函数． ‎ 理科答案 ‎1.C 2.B 3.A 4.A 5.D ‎6A 7.A 8.A 9.A 10.B 11.B 12.C ‎13. 14.ln2 15.乙 16.‎ 三、解答题（本大题共6小题，共70.0分）‎ ‎17.解： ； ； 18.解：函数的增量；‎ 函数的平均变化率． ‎ ‎19.解：， ． ， ．‎ ‎20.解：切点在切线上， 又， ，得，  ，且在点处的切线斜率为0， ，  由得，，； ， ‎ ‎． 令，则或2，‎ x ‎2‎ ‎0‎ ‎0‎ ‎40‎ ‎8‎ 故的单调增区间为：和 单调减区间为：； 由得：当时，有极大值为， 当时，有极小值为．‎ ‎21.解：根据题意，数列满足，，且， 则， ， ， ； 根据题意，由， ， ， ， ， 可归纳猜想出 ‎22.证明：要证， 只需要证明， 即 ‎， 从而只需证明，即，这显然成立． ． 如果函数在区间上，有，那么函数在其区间上为增函数， 因为函数在上有， 当时，所以函数在上是增函数．‎