【数学】2018届一轮复习人教A版高考零距离6不等式学案 3页

‎　　　　　　　　　　　　　　　　　　　　　　　　　不等式[学生用书P117]‎ 年份 卷别 具体考查内容及命题位置 ‎2016‎ 甲卷 线性规划求最值·T14‎ 乙卷 线性规划求最值·T16‎ 丙卷 线性规划求最值·T13‎ ‎2015‎ Ⅰ卷 线性规划求最值·T15‎ Ⅱ卷 线性规划求最值·T14‎ ‎2014‎ Ⅰ卷 线性规划中已知最值求参数·T11‎ Ⅱ卷 线性规划求最值·T9‎ ‎[命题分析]‎ ‎1．不等式作为高考命题热点内容之一，多以选择题、填空题的形式进行考查，直接考查时主要是简单的线性规划问题，关于不等式性质的应用、不等式的解法以及基本不等式的应用，主要体现在其工具作用上．‎ ‎2．题目多出现在第8～9或第13～15题的位置上，难度中等，但命题的模式比较固定，只要平时多加练习得分不难．‎ ‎3．若不等式与函数、导数、数列等其他知识交汇综合命题，难度较大，多出现在压轴题的位置．‎ 题示参数 真题呈现 考题溯源 题示对比 ‎(2016·高考全国卷乙，T16)某高科技企业生产产品A和产品B需要甲、乙两种新型材料．生产一件产品A需要甲材料1.5 kg，乙材料1 kg，用5个工时；生产一件产品B需要甲材料0.5 kg，乙材料0.3 kg，用3个工时．生产一件产品A的利润为2 100元，生产一件产品B的利润为900元．该企业现有甲材料150 kg，乙材料90 kg，则在不超过600个工时的条件下，生产产品A、产品B的利润之和的最大值为________元.‎ ‎(必修5 P88例5)营养学家指出，成人良好的日常饮食应该至少提供0.075 kg的碳水化合物，0.06 kg的蛋白质，0.06 kg的脂肪.1 kg食物A含有0.105 kg碳水化合物，0.07 kg蛋白质，0.14 kg脂肪，花费28元；而1 kg食物B含有0.105 kg碳水化合物，0.14 kg蛋白质，0.07 kg脂肪，花费21元．为了满足营养专家指出的日常饮食要求，同时使花费最低，需要同时食用食物A和食物B多少kg？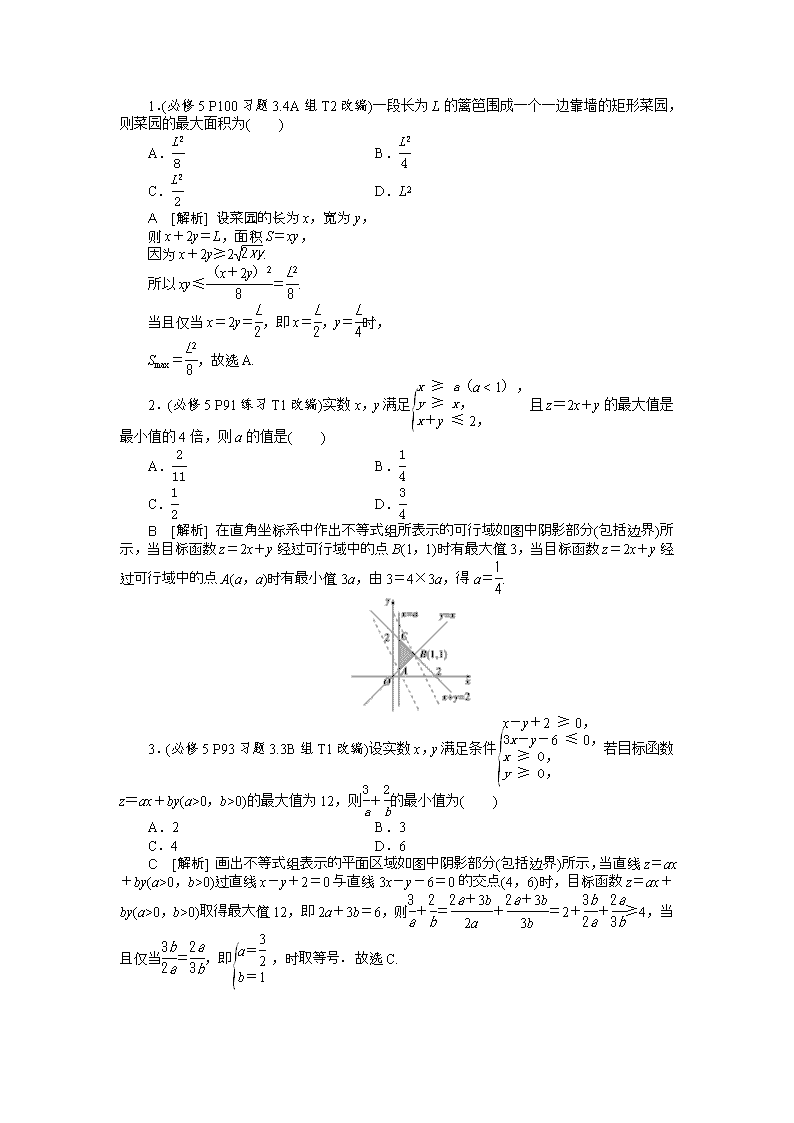‎ 题材评说 ‎(1)考题源于教材，是线性规划在实际问题中的具体应用.‎ ‎(2)考题是“闭区域”下的最大值问题，题源是“开区域”下的最小值问题.‎ ‎(3)考题是可行解(x，y)(x∈N，y∈N)(由单位件约定)的最优解，题源是可行解(x，y)(x≥0，y≥0)(由单位kg约定)的最优解问题 ‎1．(必修5 P100习题3.4A组T2改编)一段长为L的篱笆围成一个一边靠墙的矩形菜园，则菜园的最大面积为(　　)‎ A．　　　　　　　　　　　 B． C． D．L2‎ A　[解析] 设菜园的长为x，宽为y，‎ 则x＋2y＝L，面积S＝xy，‎ 因为x＋2y≥2.‎ 所以xy≤＝.‎ 当且仅当x＝2y＝，即x＝，y＝时，‎ Smax＝，故选A.‎ ‎2．(必修5 P91练习T1改编)实数x，y满足且z＝2x＋y的最大值是最小值的4倍，则a的值是(　　)‎ A． B． C． D． B　[解析] 在直角坐标系中作出不等式组所表示的可行域如图中阴影部分(包括边界)所示，当目标函数z＝2x＋y经过可行域中的点B(1，1)时有最大值3，当目标函数z＝2x＋y经过可行域中的点A(a，a)时有最小值3a，由3＝4×3a，得a＝.‎ ‎3．(必修5 P93习题3.3B组T1改编)设实数x，y满足条件若目标函数z＝ax＋by(a>0，b>0)的最大值为12，则＋的最小值为(　　)‎ A．2 B．3‎ C．4 D．6‎ C　[解析] 画出不等式组表示的平面区域如图中阴影部分(包括边界)所示，当直线z＝ax＋by(a>0，b>0)过直线x－y＋2＝0与直线3x－y－6＝0的交点(4，6)时，目标函数z＝ax＋by(a>0，b>0)取得最大值12，即2a＋3b＝6，则＋＝＋＝2＋＋≥4，当且仅当＝，即，时取等号．故选C.‎ ‎4．(必修1 P82复习参考题A组T8改编)函数f(x)＝loga(a＞0且a≠1)的定义域为________．‎ ‎[解析] 由题意得＞0，即＜0，‎ 所以－1＜x＜1.‎ 所以f(x)的定义域为(－1，1)．‎ ‎[答案] (－1，1)‎ ‎5．(必修5 P93习题3.3A组T4改编)某家电生产企业根据市场调查分析，决定调整产品生产方案，准备每周(按40个工时计算)生产空调器、彩电、冰箱共120台，且冰箱至少生产20台．已知生产这些家电产品每台所需工时和每台产值如下表：‎ 家电名称 空调器 彩电 冰箱 工时 产值/千元 ‎4‎ ‎3‎ ‎2‎ 求最高产值是多少千元．‎ ‎[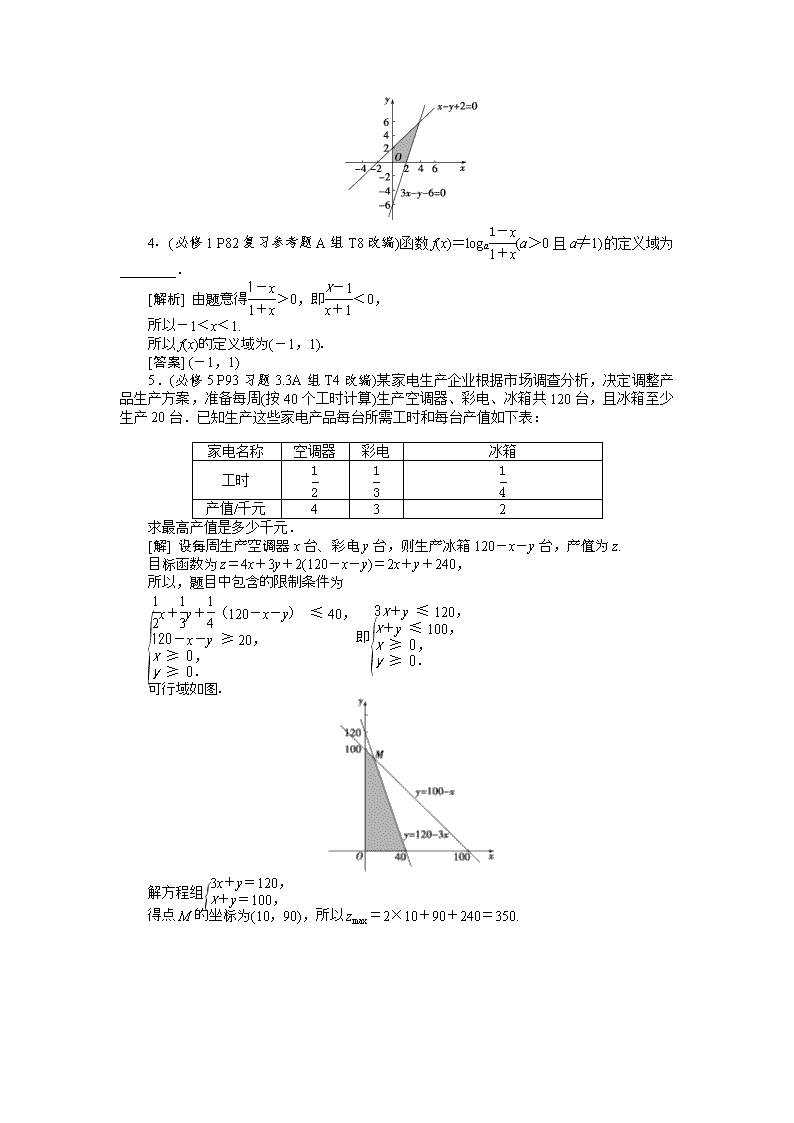解] 设每周生产空调器x台、彩电y台，则生产冰箱120－x－y台，产值为z.‎ 目标函数为z＝4x＋3y＋2(120－x－y)＝2x＋y＋240，‎ 所以，题目中包含的限制条件为 即 可行域如图．‎ 解方程组 得点M的坐标为(10，90)，所以zmax＝2×10＋90＋240＝350.‎