【数学】湖南省常德市临澧县某中学2019-2020学年高二上学期段考试卷 9页

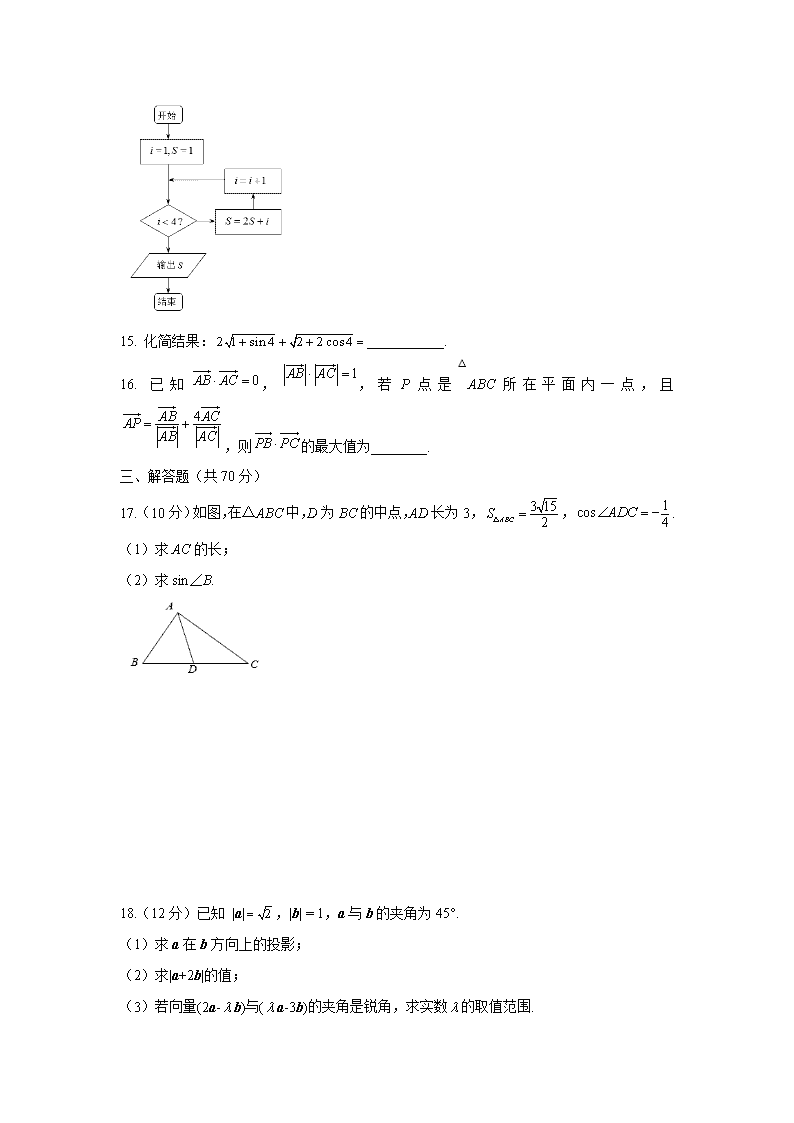
湖南省常德市临澧县某中学2019-2020学年 高二上学期段考试卷www.ks5u.com 一、选择题（5分×12）‎ ‎1. 已知集合，，则A∩B等于（ ）‎ A．(0, 2) B. (1, 2) C. (-2, 2) D. (-∞, -2)∪(0, +∞)‎ ‎2. 已知复数z的共轭复数，则复数z的虚部是（ ）‎ A． B. C. D. ‎ ‎3. 函数在区间上是增函数，则实数a的取值范围是（ ）‎ A． B. C. D. ‎ ‎4. 已知点A(2, -1)，点P(x, y)满足线性约束条件，O为坐标原点，那么的最小值是（ ）‎ A．11 B. 0 C. -1 D. -5‎ ‎5. 在区间[-3, 3]上随机取一个数x，则使得成立的概率为（ ）‎ A． B. C. D. ‎ ‎6. 函数（a>1）的图像大致是（ ）‎ A. B. C. D.‎ ‎7. 已知函数的部分图像如图所示，则函数图像的一个对称中心是（ ）‎ O ‎2‎ ‎-2‎ A． B. C. D. ‎ ‎8. 已知函数的图象的一条对称轴为直线，且，则的最小值为（ ）‎ A．0 B. C. D. ‎ ‎9. 设函数对任意的x∈R，都有，若函数 ‎，则的值是（ ）‎ A．0 B. -1 C. -2 D. -3‎ ‎10. 在锐角三角形ABC中，若，且满足关系式，则的取值范围是（ ）‎ A． B. C. D. ‎ ‎11. 已知e1, e2是单位向量，且e1·e2 =0，向量a与e1, e2共面，|a - e1 - e2 | =1，则数量积a·(a - 2e1 - 2e2) =（ ）‎ A．定值-1 B. 定值1 C. 最大值1，最小值-1 D. 最大值0，最小值11‎ ‎12. 若函数有两个不同的零点，且，则实数m的取值范围为（ ）‎ A． B. C. D. ‎ 二、填空题（5分×4）‎ ‎13. 已知|a|=|b|=2，a与b的夹角是120°，c = 2a + 3b, d = ka - 4b且c与d垂直，k的值为______.‎ ‎14. 执行如图所示的程序框图，输出的S值为_______.‎ ‎15. 化简结果：___________.‎ ‎16. 已知，，若P点是△ABC所在平面内一点，且，则的最大值为________.‎ 三、解答题（共70分）‎ ‎17.（10分）如图，在△ABC中，D为BC的中点，AD长为3，，.‎ ‎（1）求AC的长；‎ ‎（2）求sin∠B.‎ ‎18.（12分）已知 |a|，|b| = 1，a与b的夹角为45°.‎ ‎（1）求a在b方向上的投影；‎ ‎（2）求|a+2b|的值；‎ ‎（3）若向量(2a-b)与(a-3b)的夹角是锐角，求实数的取值范围.‎ ‎19.（12分）已知函数（m>0且m≠1）‎ ‎（1）求的定义域，并讨论的单调性；‎ ‎（2）若，是否存在，使在上的值域为？若存在，求出此时m的取值范围；若不存在，说明理由.‎ ‎20.（12分）已知向量a，b，且.‎ ‎（1）求a·b和|a+b|；‎ ‎（2）若函数a·b +l |a+b| 有零点，求实数的取值范围.‎ ‎21.（12分）已知函数，‎ ‎（1）求的单调增区间；‎ ‎（2）函数有两个零点，求实数a的取值范围；‎ ‎（3）A为锐角△ABC的内角，且，点M在BC上，AM为∠BAC的角平分线，AM=2，求的取值范围.‎ ‎22.（12分）已知函数，.‎ ‎（1）判断函数的奇偶性，并说明理由；‎ ‎（2）若方程有实数解，求实数k的取值范围.‎ ‎（3）若不等式在上恒成立，求实数a的取值范围.‎ ‎【参考答案】‎ 一、选择题 BADDD ABCCC AB 二、填空题 16 19 2sin2 13‎ 三、解答题 ‎17.解：（1）由，∴. …… …… …… 1分 ‎∵ ， …… …… …… 2分 即，∴DC=2. …… …… …… 3分 在△ADC中：‎ ‎，‎ ‎∴AC=4. …… …… …… 5分 ‎（2）在△ADB中：，‎ ‎ ，‎ ‎∴， …… …… …… 7分 由，∴，∴. …… …… …… 10分 ‎18. 解：（1）在方向上的投影； …… …… …… 4分 ‎（2），‎ ‎；…… …… 8分 ‎（3）与的夹角是锐角，‎ 则有，且与不共线. ‎ 而；……10分 与不共线，则有：，即，. …… …… 11分 综上所述：. …… …… ……12分 ‎19.（1）由，解得：或， …… …… …… 1分 故的定义域为：； …… …… …… 2分 ‎∵是及上的增函数. …… …… …… 4分 ‎①若，是及上的增函数；‎ ‎②若，是及上的减函数. …… …… 6分 ‎（2）显然，由（1）知时，在单调递减，‎ 据题意则有：，， ……7分 即是方程在上的两不同实根， …… …… …… 8分 方程变形为，设，‎ 则在有两个不同的零点，‎ 则有：. …… …… …… 10分 故所求m存在，. …… …… …… 12分 ‎20.解：（1）. ‎ ‎，.‎ ‎（2），‎ 令，则，‎ ‎，，显然时，. ‎ 令，则，，显然是上的增函数，‎ 在上的值域为，故.‎ ‎21.解：（1） ‎ ‎. …… …… …… 1分 由（k∈Z），‎ 即（k∈Z）时，单调递增， …… …… …… 3分 又的定义域为，故的递增区间为和； …… …… 4分 ‎（2）令，则，则该方程在上有2个根. ‎ 又时，，则有：且，‎ 解得：且，故a的取值范围是； …… …… …… 8分 ‎（3）由，∴，‎ 又，∴，∴. …… …… …… 9分 ‎∵AM为∠BAC的角平分线，故，‎ 又AM=2，在△ABM中，，∴，‎ 同理：， …… …… …… 10分 ‎∴，‎ ‎∵锐角△ABC，∴，且，∴，则，‎ 则，即的取值范围是. …… …… …… 12分 ‎22.（1），. ‎ 又， ，故是偶函数；…… …… 4分 ‎（2）由，故，∵，‎ 则，若原方程有解，则； …… …… …… 8分 ‎（3）法一：的解集为：， …… …… …… 9分 则时，或， …… …… …… 10分 又 ，即或对于恒成立，‎ ‎∴或. …… 12分 法二：由，即，显然，‎ 上述不等式等价于. …… …… …… 9分 ‎①当时，原不等式的解集为，原不等式在上恒成立，‎ 则有：，即； …… …… …… 10分 ‎②当时，原不等式的解集为，则有：，即. …… 11分 综上所述：a的取值范围是. …… …… …… 12分