2019届二轮复习专题十四　数系的扩充与复数的引入课件（12张）（全国通用） 12页

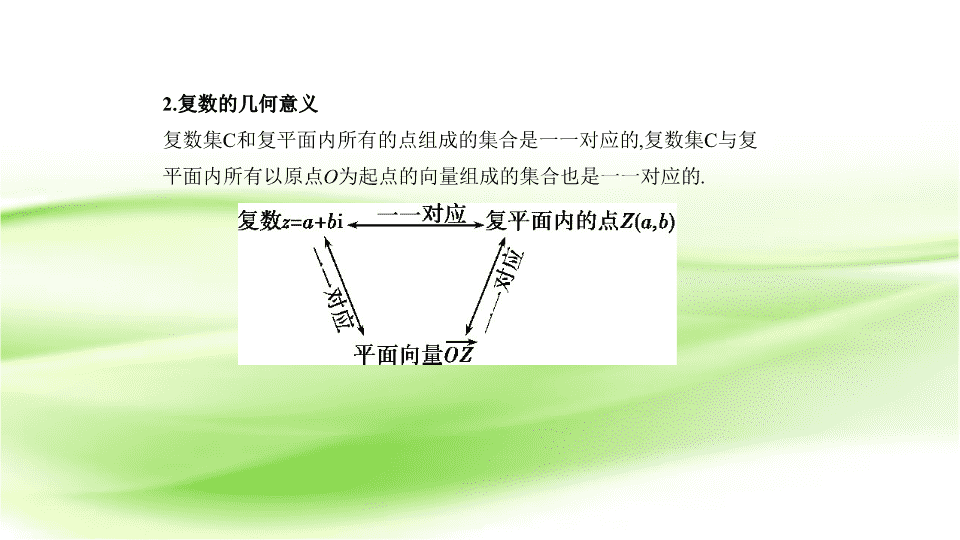
考向基础 1.复数的有关概念 考点一    复数的概念及几何意义 考点清单 2.复数的几何意义 复数集C和复平面内所有的点组成的集合是一一对应的,复数集C与复 平面内所有以原点 O 为起点的向量组成的集合也是一一对应的.   考向一    复数的有关概念问题 考向突破 例1     (2018天津十二所重点中学毕业班联考(一),9)已知复数   的实 部与虚部相等(i为虚数单位),那么实数 a = 　　　     . 解析 　∵   =   =3+ a i,其实部与虚部相等, ∴ a =3. 答案 　3 例2     (2018北京,2,5分)在复平面内,复数   的共轭复数对应的点位于   (　　) A.第一象限　    B.第二象限 C.第三象限　    D.第四象限 考向二    复数的几何意义 解析 　本题主要考查复数的概念和运算.   =   =   ,其共轭复数为   -   ,∴复数   的共轭复数对应的 点的坐标为   ,位于第四象限,故选D. 答案     D 考向基础 　　1.复数的加、减、乘、除运算法则 设 z 1 = a + b i, z 2 = c + d i( a , b , c , d ∈R),则 (1)加法: z 1 + z 2 =( a + b i)+( c + d i)=( a + c )+( b + d )i; (2)减法: z 1 - z 2 =( a + b i)-( c + d i)=( a - c )+( b - d )i; (3)乘法: z 1 · z 2 =( a + b i)·( c + d i)=( ac - bd )+( bc + ad )i; (4)除法:   =   =   =   +   i( c + d i ≠ 0). 2.复数加法的运算律 复数的加法满足交换律、结合律,即对任何 z 1 , z 2 , z 3 ∈C,有 z 1 + z 2 = z 2 + z 1 ,( z 1 + z 2 )+ z 3 = z 1 +( z 2 + z 3 ). 考点二    复数的运算 3.复数加、减法的几何意义 (1)复数加法的几何意义 若复数 z 1 、 z 2 对应的向量   、   不共线,则复数 z 1 + z 2 是以   、   为 两邻边的平行四边形的对角线   所对应的复数. (2)复数减法的几何意义 复数 z 1 - z 2 是   -   =   所对应的复数. 例     (2018课标Ⅱ,1,5分)   =   (　　) A.-   -   i　　B.-   +   i　　C.-   -   i　　D.-   +   i 考向    复数的四则运算 考向突破 解析 　本题主要考查复数的四则运算.   =   =   =-   +   i,故选D. 答案     D 方法1    复数概念的解题方法 (1)解决与复数的基本概念和性质有关的问题时,应注意复数和实数的 区别与联系,把复数问题实数化是解决复数问题的关键. (2)复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应 该满足的条件的问题,只需把复数化为 a + b i( a , b ∈R)的形式,列出实部和 虚部满足的方程(不等式)组即可. (3)解题时一定要先看复数是不是 a + b i( a , b ∈R)的形式,以确定实部和虚部. 方法技巧 例1     (2017天津,9,5分)已知 a ∈R,i为虚数单位,若   为实数,则 a 的值为 　　　     . 解析 　解法一:因为   =   =   为实数,所以-   = 0,解得 a =-2. 解法二:令   = t ( t ∈R),则 a -i= t (2+i)=2 t + t i, 所以   解得 a =-2. 答案 　-2 方法2    复数的四则运算解题方法 1.利用复数相等和相关性质将复数问题实数化是解决复数问题的常用 方法. 2.在复数代数形式的四则运算中,加、减、乘运算按多项式运算法则进 行,除法则需分母实数化. 3.在进行复数的代数运算时,记住以下结论,可提高计算速度: (1)(1 ± i) 2 = ± 2i;   =i;   =-i. (2)- b + a i=i( a + b i)( a , b ∈R). (3)i 4 n =1,i 4 n +1 =i,i 4 n +2 =-1,i 4 n +3 =-i,i 4 n +i 4 n +1 +i 4 n +2 +i 4 n +3 =0, n ∈N * . 例2　 (1)(2018课标Ⅰ,1,5分)设 z =   +2i,则| z |=   (　　) A.0　    B.   　    C.1　    D.   (2)已知复数 z =1+   ,则1+ z + z 2 + … + z 2 018 = 　　　     . 解析 　(1)∵ z =   +2i=   +2i=i,∴| z |=1,故选C. (2)解法一:(根据等比数列的前 n 项和公式求解) 因为 z =1+   =1+   =i,所以1+ z + z 2 + … + z 2 018 =   =   =   =i. 解法二:(利用周期性求解)因为 z =1+   =1+   =i,所以1+ z + z 2 + … + z 2 0 18 =1+i+i 2 + … +i 2 018 =504 × (1+i-1-i)+1+i-1=i. 答案 　(1)C　(2)i