【数学】宁夏银川市第六中学2020届高三第三次月考试卷（文） 10页

宁夏银川市第六中学2020届高三第三次月考 数学试卷（文）‎ 一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只 有一项是符合题目要求的．‎ ‎1．已知集合，则CRA=（ ）‎ A． B． C． D．‎ ‎2．设复数z满足z（2-i）=1+i(i为虚数单位)，则z的共轭的虚部为（ ）‎ A． B． C． D． ‎ ‎3．若某程序框图如图所示，则该程序运行后输出的（ ）‎ A．4 B．13 ‎ C．40 D．41‎ ‎4．已知等差数列{an},若a2=10,a5=1,则{an}的前7项和为（ ）‎ A．112 B．51 C．28 D．18‎ ‎5．已知，，，若，则= （ ）‎ A．-5 B．5 C．1 D．-1‎ ‎6．甲、乙、丙三人参加银川一中招聘老师面试，最终只有一人能够被银川一中录用，得到 面试结果后，甲说：“丙被录用了”；乙说：“甲被录用了”；丙说：“我没被录用”。若这三人 中仅有一人说法错误，则下列结论正确的是（ ）‎ A．丙被录用了 B．乙被录用了 C．甲被录用了 D．无法确定谁被录用了 ‎7．已知（ ）‎ A． B． C． D．‎ ‎8．若，则的最小值为（ ）‎ A．4 B．5 C．7 D．6‎ ‎9．已知m, n是空间中两条不同的直线，α，β为空间中两个互相垂直的平面，则下列命题正 确的是（ ）‎ A． B． ‎ C． D．若，则 ‎ ‎10．在棱长为1的正方体ABCD-A1B1C1D1中，点E，F分别是侧面AA1D1D与底面ABCD的 中心，则下列说法错误的个数为（ ）‎ ①DF∥平面D1EB1； ②异面直线DF与B1C所成的角为600；‎ ③ED1与平面B1DC垂直; ④ ‎ A． 0 B．1 C．2 D．3‎ ‎11．已知函数在上可导且满足，则下列一定成立的为（ ）‎ A． B． ‎ C． D．‎ ‎12．黄金三角形就是一个等腰三角形，其顶角为 36°，底角为 72°，底与腰的长度比值约为 ‎0.618，这一数值也可以表示为m=2cos72°，若n=cos360cos720cos1440，则mn=（ ）‎ A．-1 B． Ｃ． Ｄ．1‎ 二．填空题（本题共4小题，每小题5分，共20分）‎ ‎13．曲线y=2lnx在点（1，0）处的切线方程为________.‎ ‎14．设，满足约束条件，则的最大值是______.‎ ‎15．已知数列满足Sn=n2+2n+1，则an=________.‎ ‎16．某几何体的三视图如图所示，则该几何体的内切球的半径为______． ‎ 三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第22、23为选考题，考生根据要求作答.‎ ‎（一）必考题：共60分.‎ ‎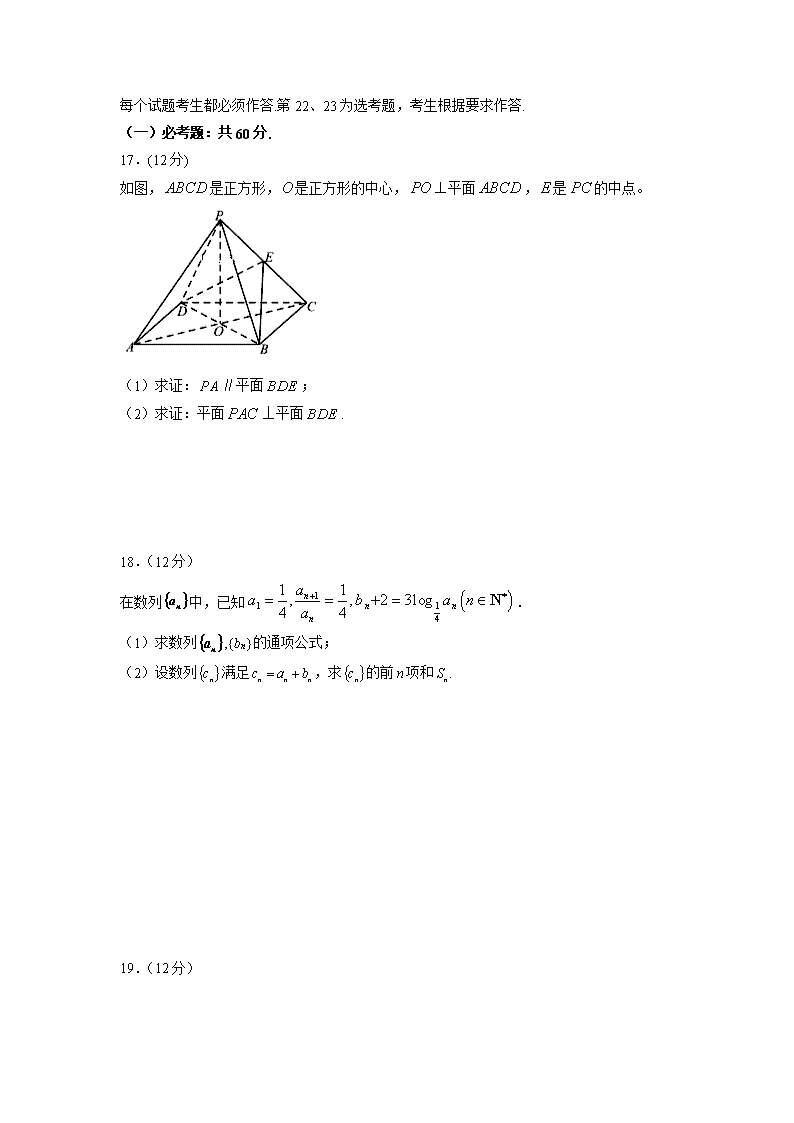17．(12分)‎ 如图，是正方形，是正方形的中心，平面，是的中点。‎ ‎（1）求证：∥平面； ‎ ‎（2）求证：平面⊥平面.‎ ‎18．（12分）‎ 在数列中，已知．‎ ‎（1）求数列,{bn}的通项公式；‎ ‎（2）设数列满足，求的前项和.‎ ‎19．（12分）‎ 如图所示，在ΔABC中，，，，.‎ ‎（1）求证：ΔABD是等腰三角形;‎ ‎（2）求的值以及的面积.‎ ‎20．（12分）‎ 如图，在三棱柱ABC—A1B1C1中，∠BAC=，AA1丄平面ABC，AB=AC，E是线段BB1上的动点，D是线段BC的中点。‎ ‎(1)证明：AD丄C1E；‎ ‎(2)若AB = 2, AA1=,且直线AC、C1E所成角的余弦值为,试指出点E在线段BB1上的位置，并求三棱锥B1-A1DE的体积.‎ ‎21．(12分)‎ 已知函数．‎ ‎（1）设是函数的极值点，求的值，并求的单调区间；‎ ‎（2）若对任意的，恒成立，求的取值范围．‎ ‎(二)选考题：共10分.请考生在第22、23两题中任选一题做答，如果多做．则按所做的第一题记分.‎ ‎22．[选修4－4：坐标系与参数方程]‎ 在平面直角坐标系中，曲线的参数方程（为参数）．以为极点，轴的非负半轴为极轴建立极坐标系．‎ ‎（1）求曲线的极坐标方程；‎ ‎（2）若直线的极坐标方程是，射线与曲线的交点为，与直线的交点为，求线段的长．‎ ‎23．[选修4－5：不等式选讲]‎ 已知函数 ‎（1）解不等式；‎ ‎（2）若，求证：.‎ 参考答案 ‎1-5 DBCCA 6-10 CBCDA 11．C 12．B ‎13．2x-y-2=0 14． 7 15． 16． 20‎ ‎17. (1)证明　连接OE，如图所示．‎ ‎∵O、E分别为AC、PC的中点，∴OE∥PA．‎ ‎∵OE⊂面BDE，PA⊄面BDE，‎ ‎∴PA∥面BDE．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6分 ‎(2)证明　∵PO⊥面ABCD，∴PO⊥BD．‎ 在正方形ABCD中，BD⊥AC，又∵PO∩AC＝O，∴BD⊥面PAC．‎ 又∵BD⊂面BDE，∴面PAC⊥面BDE．．．．．．．．．．．．．．．．．．．．12分 ‎18．解：（1）,∴数列是首项为，公比为的等比数列，‎ ‎∴．‎ 因为，所以．‎ ‎（2）由（1）知，, 所以 ‎ 所以 ‎ ‎ ‎．‎ ‎19.解：‎ ‎20．解：（1）根据图象可知 代入得，，‎ 把函数的图像向右平移个单位长度，再向下平移1个单位，得到函数 ‎，设，则，‎ 此时，所以值域为．‎ ‎（2）由（1）可知 ‎ 对任意都有恒成立 令，‎ ‎，是关于的二次函数，开口向上 则恒成立 而的最大值，在或时取到最大值 则，，‎ 解得 所以，则的最大值为．‎ ‎21．解：（1）由题意，函数，‎ 则，‎ 因为是函数的极值点，所以，故，‎ 即，令，解得或．‎ 令，解得,‎ 所以在和上单调递增，在上单调递减．‎ ‎（2）由，‎ 当时，，则在上单调递增，‎ 又，所以恒成立；‎ 当时，易知在上单调递增，‎ 故存在，使得，‎ 所以在上单调递减，在上单调递增，‎ 又，则，这与恒成立矛盾．‎ 综上，．‎ ‎22．解：(1)曲线的普通方程为 ，极坐标方程为 ------4分 ‎(2)设，则有解得 -------6分 设，则有解得--------8分 所以 ． --10分 ‎23．（I）解：∵|x﹣m|+|x|≥|x﹣m﹣x|=|m|，‎ ‎∴要使|x﹣m|+|x|＜2有解，则|m|＜2，解得﹣2＜m＜2．‎ ‎∵m∈N*，∴m=1．（5分）‎ ‎（II）证明：α，β＞0，f（α）+f（β）=2α﹣1+2β﹣1=2，‎ ‎∴α+β=2．‎ ‎∴+==≥=，‎ 当且仅当α=2β=时取等号．（10分）‎