【数学】2021届一轮复习人教A版导数常用的一些技巧和结论学案 10页

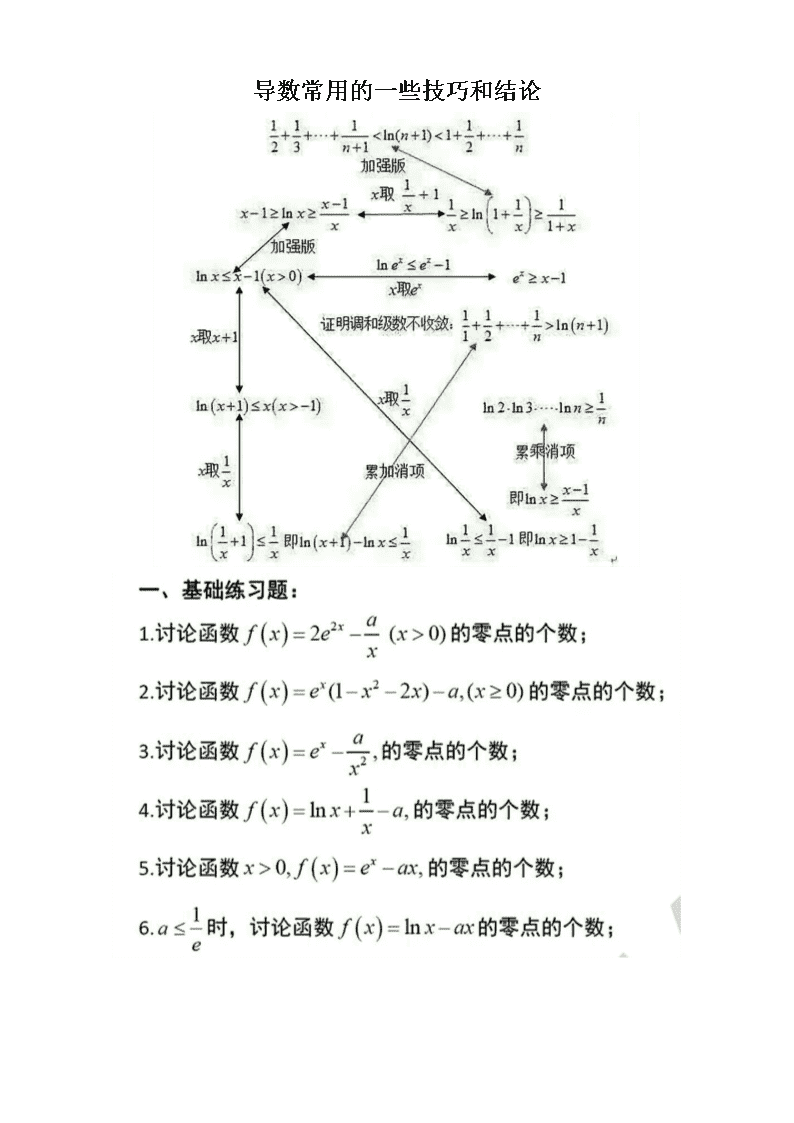
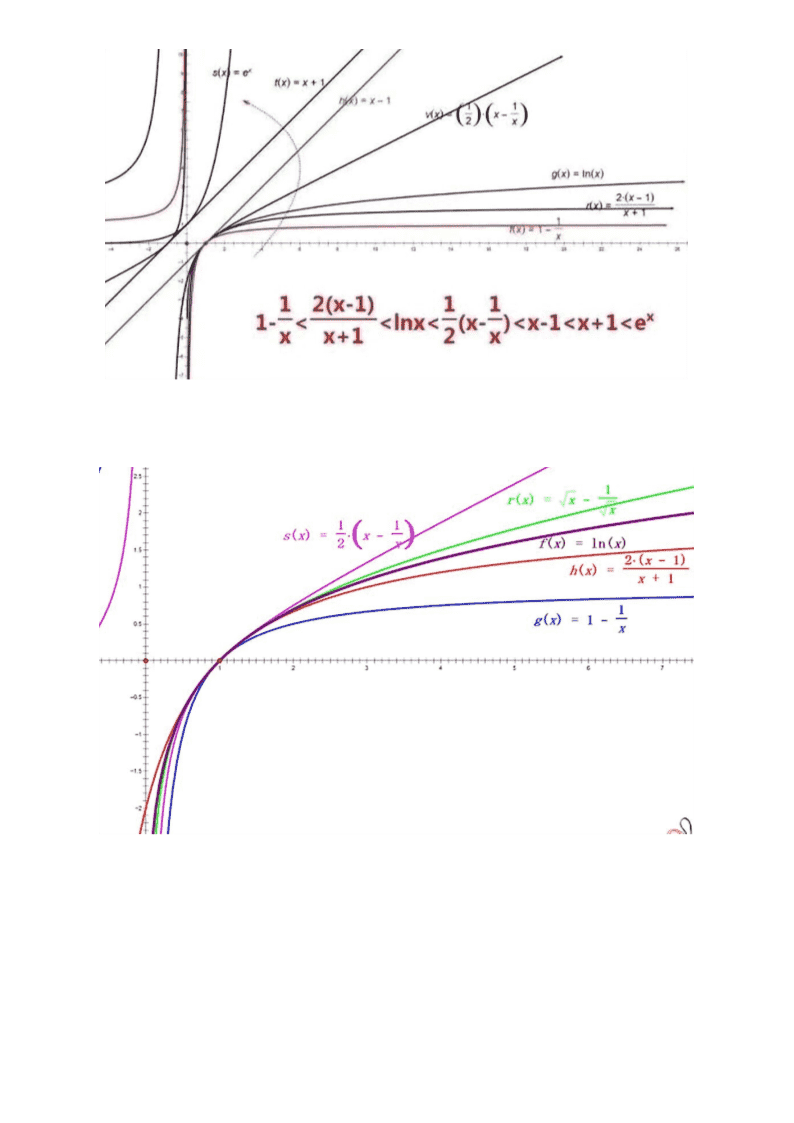
导数常用的一些技巧和结论 ‎（2018年全国新课标1·理·21）已知.‎ ‎（1）讨论的单调性；‎ ‎（2）若有两个零点，求的取值范围.‎ 解析：（1）‎ 若，则恒成立，所以在R上递减；‎ 若，令，得.‎ 当时，，所以在上递减；‎ 当时，，所以在上递增.‎ 综上，当时，在R上递减；当时，在上递减，在上递增.‎ ‎（2）有两个零点，必须满足，即，且.‎ 构造函数，. 易得，所以单调递减.‎ 又因为，所以.‎ 下面只要证明当时，有两个零点即可，为此我们先证明当时，.‎ 事实上，构造函数，易得，∴，所以，即.‎ 当时，，‎ ‎，‎ 其中，，所以在和上各有一个零点.‎ 故的取值范围是.‎ 注意：取点过程用到了常用放缩技巧。‎ 一方面：；‎ 另一方面：时，（目测的）‎ 常用的放缩公式（考试时需给出证明过程）‎ 第一组：对数放缩 ‎（放缩成一次函数），，‎ ‎（放缩成双撇函数），，‎ ‎，，‎ ‎（放缩成二次函数），，‎ ‎（放缩成类反比例函数），，，‎ ‎，，‎ 第二组：指数放缩 ‎（放缩成一次函数），，，‎ ‎（放缩成类反比例函数），，‎ ‎（放缩成二次函数），，‎ 第三组：指对放缩 第四组：三角函数放缩 ‎，，. ‎ 第五组：以直线为切线的函数 ‎，，，，.‎ 几个经典函数模型 经典模型一：或.‎ ‎【例1】讨论函数的零点个数.‎ ‎（1）时，无零点.‎ ‎，.‎ ‎（2）时，1个零点.‎ ‎，.‎ ‎（3）当时，2个零点.‎ ‎（目测），，其中.（放缩）‎ ‎.‎ ‎，其中.（用到了）‎ ‎（4）当时，1个零点.‎ ‎，单调递增.，‎ ‎.‎ ‎【变式】（经过换元和等价变形之后均可以转化到例1：）：‎ ‎1. 讨论的零点个数（令，）；‎ ‎2. 讨论的零点个数（令）；‎ ‎3. 讨论的零点个数（考虑）；‎ ‎4. 讨论的零点个数（考虑，令，）；‎ ‎5. 讨论的零点个数（令，）；‎ ‎6. 讨论的零点个数（令）.‎ 经典模型二：或 ‎【例2】讨论函数的零点个数.‎ ‎（1）时，1个零点.‎ ‎，单调递增.‎ 且，，所以在上有一个零点；‎ ‎（2）时，无零点.‎ 恒成立；‎ ‎（3）时，无零点.‎ ‎；‎ ‎（4）时，2个零点.‎ ‎，，.‎ ‎【变式】（经过换元和等价变形之后均可以转化到例题2：）：‎ ‎1. 讨论的零点个数（令，）；‎ ‎2. 讨论的零点个数（去分母后与1等价）；‎ ‎3. 讨论的零点个数（移项平方后与1等价）；‎ ‎4. 讨论的零点个数（移项开方后换元与1等价）；‎ ‎5. 讨论的零点个数（乘以系数e，令）；‎ ‎6. 讨论的零点个数（令，转化成2）‎ ‎7. 讨论的零点个数（令，）；‎ 经典模型三：或 ‎【例】讨论函数的零点个数.‎ ‎（1）时，1个零点. ‎ ‎，单调递增.‎ ‎，.‎ ‎（2）时，1个零点（）.‎ ‎（3）时，无零点.‎ ‎，‎ ‎（4）时，1个零点.‎ ‎.‎ ‎（5）时，2个零点.‎ ‎，，，‎ ‎【变式】（经过换元和等价变形之后均可以转化到例题3：）：‎ ‎1.讨论的零点个数；‎ ‎2. 讨论的零点个数（考虑，令）；‎ ‎3. 讨论的零点个数（令）；‎ ‎4. 讨论的零点个数；‎ 练习题 ‎1. 已知函数有两个零点，求的取值范围.‎ ‎2. 设函数，讨论的导函数的零点的个数.‎ ‎3. 已知函数有两个零点，求的取值范围.‎ ‎4.已知函数. 当时，试讨论的零点的个数.‎