2020届二轮复习抛物线课件课件（全国通用） 17页

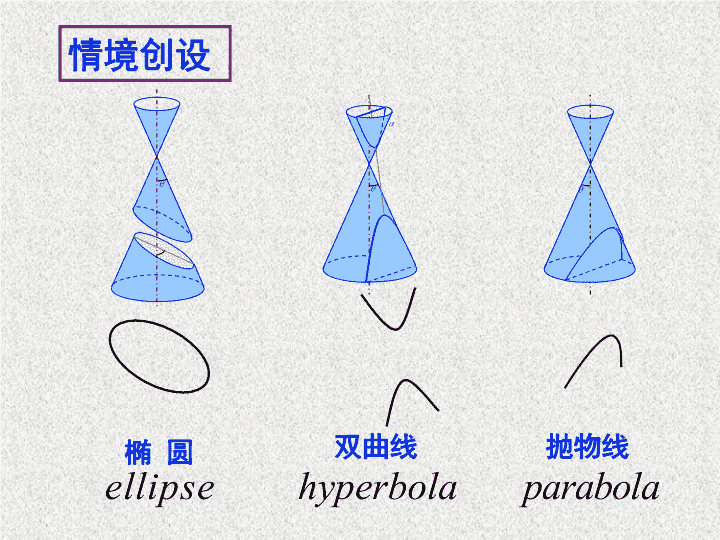
    椭 圆 双曲线 抛物线 情境创设 2.4 抛物线 2.4 抛物线 如何确定抛物线的标准方程？ 抛物线有哪些几何性质？ 知识回顾 · · F M l N 抛物线的定义： 平面内与一个定点 F 和一条定直线 l （点 F 不在直线 l 上 ）的距离相等的点的轨迹叫做 抛物线 . 定点 F 叫做抛物线的 焦点 (focus) . 定直线 l 叫做抛物线的 准线 (directrix) . 数学建构 · · F M l N 设焦点 F 到准线 l 的距离为 p ① MF = MN ② 探究 : 如何建立平面直角坐标系？ 抛物线的标准方程 ． y x o ﹒ y x o ﹒ y x o ﹒ ﹒ y x o ） ） 图像 方程 焦点 准 线 问题 1 ： 已知抛物线的标准方程是 y 2 = 6x ， 求它的焦点坐标和准线方程； 变题： 已知抛物线的方程是 y = － 6x 2 ，求它的焦点坐标和准线方程 . 数学应用 变题 2: 求过点 A （ -3 ， 2 ）的抛物线的标准方程 . 问题 2 ： 已知抛物线的焦点坐标是 F （ 0 ， -2 ），求它的标准方程 . 数学应用 变题 1 ： 已知抛物线顶点在原点，对称轴为坐标轴，焦点在直线 上，求它的标准方程 . 1 、根据下列条件，写出抛物线的标准方程： （ 1 ）焦点是 F （ 3 ， 0 ）； （ 2 ）准线方程是 ； （ 3 ）焦点到准线的距离是 2 。 学生活动 2 、求下列抛物线的焦点坐标和准线方程： 焦点坐标 准线方程 本节课你有哪些收获？ 本节课你还有哪些困惑？ 本节课你有哪些收获？ 问题 3 ： 若抛物线 有一点 M(6,6) ，求点 M 到焦点的距离 . 变题 1 ： M 是抛物线 y 2 = 2px （ P ＞ 0 ）上一点，若点 M 的横坐标为 X 0 ，求点 M 到焦点的距离。 数学拓展 变题 2 ： 若抛物线 上有一点 M ，若点 M 的横坐标为 9 ，它到焦点的距离是 10 ， 求抛物线方程和 M 点的坐标 . 问题 3 ：若抛物线 有一点 M ，其横坐标为 6 ，求点 M 到焦点的距离 . 变题 1 ： M 是抛物线 y 2 = 2px （ P ＞ 0 ）上一点，若点 M 的横坐标为 X 0 ，求点 M 到焦点的距离 . 数学拓展