【数学】2020届一轮复习人教版（理）第2章第5讲指数与指数函数学案 11页

第5讲　指数与指数函数 ‎[考纲解读]　1.理解有理指数幂的含义，掌握指数幂的运算，并能通过具体实例了解实数指数幂的意义．‎ ‎2.理解指数函数的概念，理解指数函数的单调性并掌握指数函数的图象及其通过的特殊点．(重点、难点)‎ ‎3.通过具体实例，了解指数函数模型的实际背景，并体会指数函数是一类重要的函数模型．‎ ‎[考向预测]　从近三年高考情况来看，本讲是高考中的命题热点．预测2020年高考主要与函数的图象、最值、比较大小、指数函数图象过定点为命题方向；也有可能与其他知识相结合进行考查.‎ ‎1．根式 ‎2．有理数指数幂 ‎(1)幂的有关概念 ‎①正数的正分数指数幂：a＝(a>0，m，n∈N*且n>1)．‎ ‎②正数的负分数指数幂：a－＝＝(a>0，m，n∈N*且n>1)．‎ ‎③0的正分数指数幂等于0；0的负分数指数幂没有意义．‎ ‎(2)有理数指数幂的性质 ‎①aras＝ar＋s(a>0，r，s∈Q)；‎ ‎②(ar)s＝ars(a>0，r，s∈Q)；‎ ‎③(ab)r＝arbr(a>0，b>0，r∈Q)．‎ ‎3．指数函数的图象与性质 y＝ax (a>0且a≠1)‎ a>1‎ ‎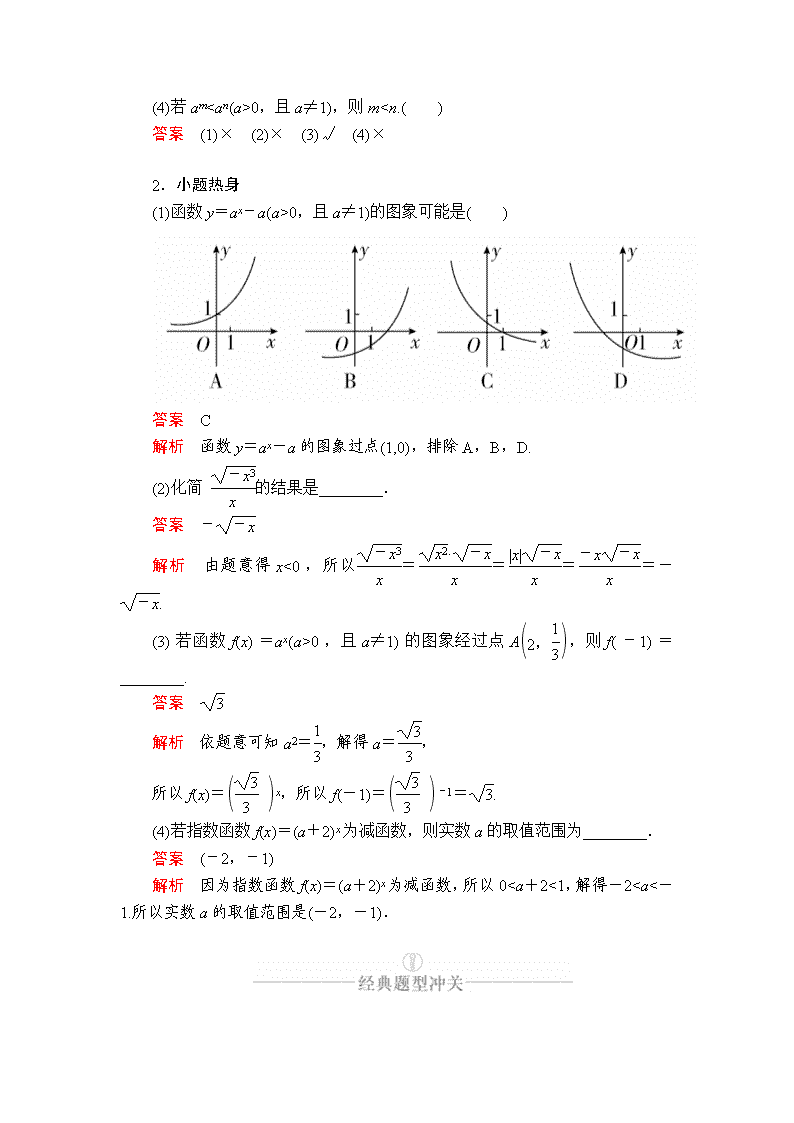00，且a≠1)，则m0，且a≠1)的图象可能是(　　)‎ 答案　C 解析　函数y＝ax－a的图象过点(1,0)，排除A，B，D.‎ ‎(2)化简 的结果是________．‎ 答案　－ 解析　由题意得x<0，所以＝＝＝＝－.‎ ‎(3)若函数f(x)＝ax(a>0，且a≠1)的图象经过点A，则f(－1)＝________.‎ 答案　 解析　依题意可知a2＝，解得a＝，‎ 所以f(x)＝x，所以f(－1)＝－1＝.‎ ‎(4)若指数函数f(x)＝(a＋2)x为减函数，则实数a的取值范围为________．‎ 答案　(－2，－1)‎ 解析　因为指数函数f(x)＝(a＋2)x为减函数，所以00，a≠1)的图象恒过点A，下列函数中图象不经过点A的是(　　)‎ A．y＝ B．y＝|x－2|‎ C．y＝2x－1 D．y＝log2(2x)‎ 答案　A 解析　函数f(x)＝ax－1(a>0，且a≠1)的图象恒过点A(1,1)，经检验知，只有选项A中函数的图象不经过点A.‎ ‎2．(2018·青岛模拟)函数f(x)＝21－x的大致图象为(　　)‎ 答案　A 解析　函数f(x)＝21－x在R上是减函数，其图象过点(0,2)，故选A.‎ 条件探究1　举例说明2中函数改为f(x)＝2|x－1|，其图象是(　　)‎ 答案　B 解析　f(x)＝2|x－1|＝ 所以f(x)在(－∞，1]上单调递减，在(1，＋∞)上单调递增，故排除A，C，D.‎ 条件探究2　举例说明2中函数改为y＝21－x＋m，若此函数的图象不经过第一象限，则m的取值范围如何？‎ 解　因为y＝21－x＋m＝x－1＋m，函数y＝x－1的图象如图所示，‎ 则要使函数y＝21－x＋m的图象不经过第一象限，则m≤－2.‎ ‎(1)画指数函数y＝ax(a>0，且a≠1)的图象，应抓住三个关键点：(1，a)，(0,1)，.如举例说明1.‎ ‎(2)指数函数图象的应用 ‎①已知函数解析式判断其图象一般是取特殊点，判断选项中的图象是否过这些点，若不满足则排除．‎ ‎②对于有关指数型函数的图象问题，一般是从最基本的指数函数的图象入手，通过平移、伸缩、对称变换而得到．特别地，当底数a与1的大小关系不确定时应注意分类讨论．‎ ‎(3)指数函数在同一坐标系中的图象的相对位置与底数大小关系 如图所示，其中0b>c B．b>a>c C．c>a>b D．c>b>a 答案　A 解析　因为a＝(22)0.8＝21.6，b＝(23)0.46＝21.38，c＝(2－1)－1.2＝21.2，‎ 函数y＝2x在R上单调递增，且1.2<1.38<1.6，‎ 所以21.2<21.38<21.6，即c0，即a<1时，41－a＝‎2a－(a－1)，解得a＝；当1－a<0，即a>1时，‎2a－(1－a)＝‎4a－1，此方程无解．综上所述，a＝.‎ ‎3．不等式2－x2＋2x>x＋4的解集为________．‎ 答案　{x|－1x＋4，‎ ‎∴ x2－2x >x＋4，‎ ‎∴x2－2x0，且a≠1)型函数最值问题多用换元法，即令t＝ax转化为y＝t2＋bt＋c的最值问题，注意根据指数函数求t的范围．‎ ‎(2)形如y＝af(x)(a>0，且a≠1)型函数最值问题，可令t＝f(x)，则y＝at，先由x的取值范围求t的取值范围，再求y＝at的最值．如举例说明4.‎ ‎4．对于形如y＝af(x)的函数的单调性 ‎(1)若a>1，函数f(x)的单调增(减)区间即函数y＝af(x)的单调增(减)区间；‎ ‎(2)若0b>c B．a>c>b C．c>a>b D．b>c>a 答案　A 解析　∵指数函数y＝0.4x为减函数，0.2<0.6，‎ ‎∴‎0.40.2‎>0.40.6，∴b>c.‎ ‎∵幂函数y＝x0.2为增函数，2>0.4，‎ ‎∴20.2>‎0.40.2‎，‎ ‎∴a>b，∴a>b>c.‎ ‎2．函数f(x)＝－x2＋2x＋1的单调减区间为________．‎ 答案　(－∞，1]‎ 解析　设u＝－x2＋2x＋1，‎ 因为y＝u在R上为减函数，‎ 所以函数f(x)＝－x2＋2x＋1的单调减区间即为函数u＝－x2＋2x＋1的单调增区间．‎ 又u＝－x2＋2x＋1的单调增区间为(－∞，1]，‎ 所以f(x)的单调减区间为(－∞，1]．‎ ‎3．设函数f(x)＝若f(a)<1，则实数a的取值范围是________．‎ 答案　(－3,1)‎ 解析　当a<0时，不等式f(a)<1可化为a－7<1，‎ 即a<8，即a<－3，‎ ‎∴a>－3.又a<0，∴－3