新教材数学北师大版（2019）必修第二册课件：阶段提升课 第五课　复数 课件（16张） 16页

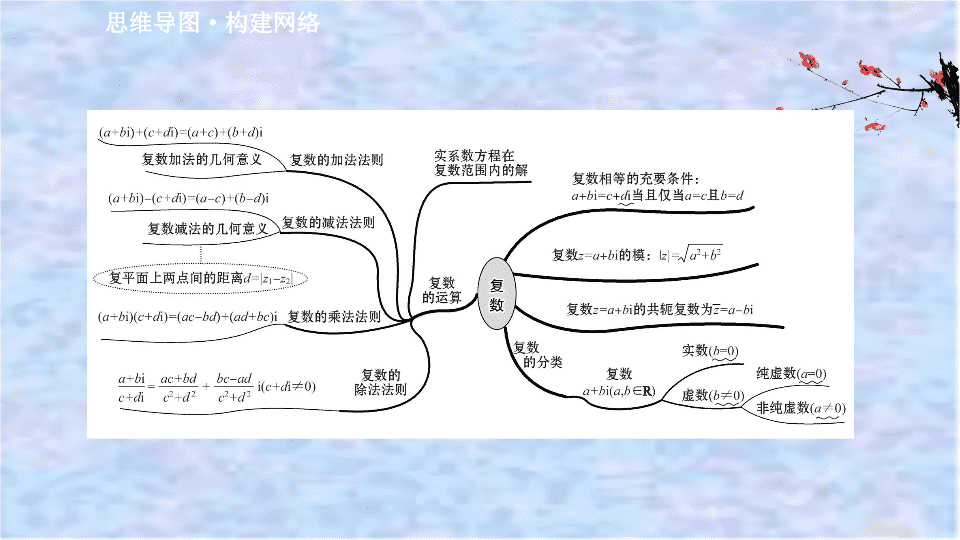
阶段提升课 第五课　复　　数 思维导图·构建网络 考点整合·素养提升 题组训练一　复数的概念问题  1.i是虚数单位,复数z= 为纯虚数,则实数a为 (　　) A.-2　 B.2 C.- 　 D. (a i)(1 2i)  1 2 1 2 2.若复数z= ,其中i为虚数单位,则下列结论正确的是 (　　) A.z的虚部为-i B.|z|=2 C.z2为纯虚数 D.z的共轭复数为-1-i 2 1 i 3.当实数a为何值时,z=a2-2a+(a2-3a+2)i. (1)为实数;(2)为纯虚数; (3)对应的点在第一象限内; (4)复数z对应的点在直线x-y=0上. 【解析】1.选B.因为z= 为纯虚数,所以 解得a=2 . 2.选C.由题意得z= 对于A,由z=1-i得复数z的虚部为-1,所以A不正确.对于B,|z|=|1-i|= ,所以 B不正确. 对于C,由于z2=(1-i)2=-2i,所以z2为纯虚数,所以C正确.对于D,z=1-i的共轭复 数为 =1+i,所以D不正确. (a i)(1 2i) (a 2) (2a 1)i    － a 2 0 2a 1 0     － ， ，   2 2(1 i) 1 i1 i 1 i (1 i)    － － ．－ 2 z 3.(1)z∈R⇔a2-3a+2=0,解得a=1或a=2. (2)z为纯虚数, 即 故a=0. (3)z对应的点在第一象限,则 所以 所以a<0,或a>2. 所以a的取值范围是(-∞,0)∪(2,+∞). (4)依题设(a2-2a)-(a2-3a+2)=0,所以a=2. 2 2 a 2a 0 a 3a 2 0   － ＝ ， － ＋ ， a 0 a 2 a 1 a 2.     ＝ 或 ＝ ， 且 2 2 a 2a 0 a 3a 2 0    － ， － ＋ ， a 0 a 2 a 1 a 2      ，或 ， ，或 ， 【方法技巧】 　处理复数概念问题的两个注意点 (1)当复数不是a+bi(a,b∈R)的形式时,要通过变形化为a+bi的形式,以便确定其 实部和虚部. (2)求解时,要注意实部和虚部本身对变量的要求,否则容易产生增根. 题组训练二　复数的几何意义  1.复数z= (i为虚数单位)在复平面内对应点的坐标是 (　　) 2.已知复数z1=2+3i,z2=a+bi,z3=1-4i,它们在复平面上所对应的点分别为 A,B,C.若 则a=________,b=________.  2 4i 1 i  － A 3,3 B 1,3 C 3, 1 D 1,3．( ) ．( ) ．( － ) ．(－ ) OC 2OA OB    ＝ ＋ ， 【解析】1.选D.因为z= 所以z在复平面内对应点的坐标是 2.因为 所以1-4i=2(2+3i)+(a+bi), 即 所以 答案:-3　-10 2 4i (2 4i)(1 i) 1 3i1 i 2     － ，－ 1,3(－ )． OC 2OA OB    ＝ ＋ ， 1 4 a 4 6 b    ＝ ＋ ， － ＝ ＋ ， a 3 b 10.    ＝－ ， ＝－ 【方法技巧】 　在复平面内确定复数对应点的步骤 (1)由复数确定有序实数对,即z=a+bi(a,b∈R)确定有序实数对(a,b). (2)由有序实数对(a,b)确定复平面内的点(a,b). 题组训练三　复数的四则运算  1.已知 是z的共轭复数,若z· i+2=2z,则z=(　　) A.1+i　 B.1-i C.-1+i　　 D.-1-i 2.已知复数z1=2-3i,z2= ,则 =(　　) A.-4+3i　 B.3+4i C.3-4i　　 D.4-3i z z 2 3 2i (2 i) ＋ ＋ 1 2 z z 【解析】1.选A.设z=a+bi(a,b∈R), 则 =a-bi,代入z· i+2=2z中得,(a+bi)(a-bi)i+2=2(a+bi),所以 2+(a2+b2)i=2a+2bi, 由复数相等的条件得, 所以 所以z=1+i. z z 2 2 2a 2 a b 2b    ＝ ， ＋ ＝ ， a 1 b 1.    ＝ ， ＝ 2.选D. 2 1 2 z (2 3i)(2 i) z 3 2i － ＋＝ ＋    22 3i 3 2i 2 i (3 2i)(3 2i)    ＝ ＋ － 13i(3 4i) 4 3i.13 － ＋＝ ＝ － 【方法技巧】 　进行复数代数运算的策略 (1)复数代数形式的运算的基本思路就是应用运算法则进行计算. (2)复数的四则运算中含有虚数单位i的看作一类同类项,不含i的看作另一类 同类项,分别合并即可,但要注意把i的幂写成最简形式. (3)利用复数相等可实现复数问题的实数化.