【数学】2020届一轮复习人教A版直线、平面垂直的判定和性质考点 10页

直线、平面垂直的判定和性质 ‎ 审稿: ‎ ‎【考纲要求】‎ ‎1、掌握直线和平面垂直的判定定理和性质定理； ‎ ‎2、掌握两个平面垂直的判定定理和性质定理．‎ ‎3、能运用公理、定理和已经获得的结论证明一些空间图形的垂直关系的简单命题。‎ ‎【知识网络】‎ 直线、平面垂直 判定定理 性质定理 线面垂直 面面垂直 判定定理 性质定理 ‎【考点梳理】‎ 考点一、直线与平面垂直的判定 ‎1、定义：如果直线与平面α内的任意一条直线都垂直，则直线与平面α垂直；‎ ‎2、判定定理：‎ ‎（1）内容：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；‎ ‎（2）符合语言：‎ ‎ ‎ ‎3、证明直线和平面垂直的常用方法有：‎ ‎（1）利用判定定理；‎ ‎（2）利用平行线垂直于平面的传递性 ‎（3）利用面面平行的性质 ‎（4）利用面面垂直的性质。‎ 要点诠释：‎ 当直线和平面垂直时，该直线垂直于平面内的任一直线，常用来证明线线垂直。‎ 考点二、直线与平面垂直的性质 1、 如果两条直线同垂直于一个平面,那么这两条直线平行。‎ 2、 如果两条平行线中有一条垂直于一个平面，那么另外一条也垂直于这个平面。‎ 考点三、平面与平面垂直的判定 ‎1、二面角的有关概念 ‎（1）二面角：从一条直线出发的两个半平面所组成的图形叫做二面角；‎ ‎（2）二面角的平面角：以二面角的棱上任一点为端点，在两个半平面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角。‎ ‎2、平面与平面垂直 ‎（1）定义：如果两个平面所成的二面角是直二面角，就说这两个平面互相垂直；‎ ‎（2）判定定理：一个平面过另一个平面的垂线，则这两个平面垂直；‎ ‎（3）符号语言：‎ ‎3、证明面面垂直的主要方法是：‎ ‎①利用判定定理。在审题时要注意直观判断哪条直线可能是垂线，充分利用等腰三角形底边的中线垂直于底边，勾股定理等结论。‎ ‎②用定义证明。只需判定两平面所成二面角为直二面角。‎ ‎③客观题中，也可应用：两个平行平面中的一个垂直于第三个平面，则另一个也垂直于第三个平面。‎ 考点四、平面与平面垂直的性质 ‎1、判定定理：若两个平面互相垂直，那么在一个平面内垂直于它们的交线的直线垂直于另一个平面 ‎ ‎2、符号语言：‎ 要点诠释：立体几何中垂直问题的证明，通常是从线线垂直切入，然后向线面垂直或面面垂直延伸。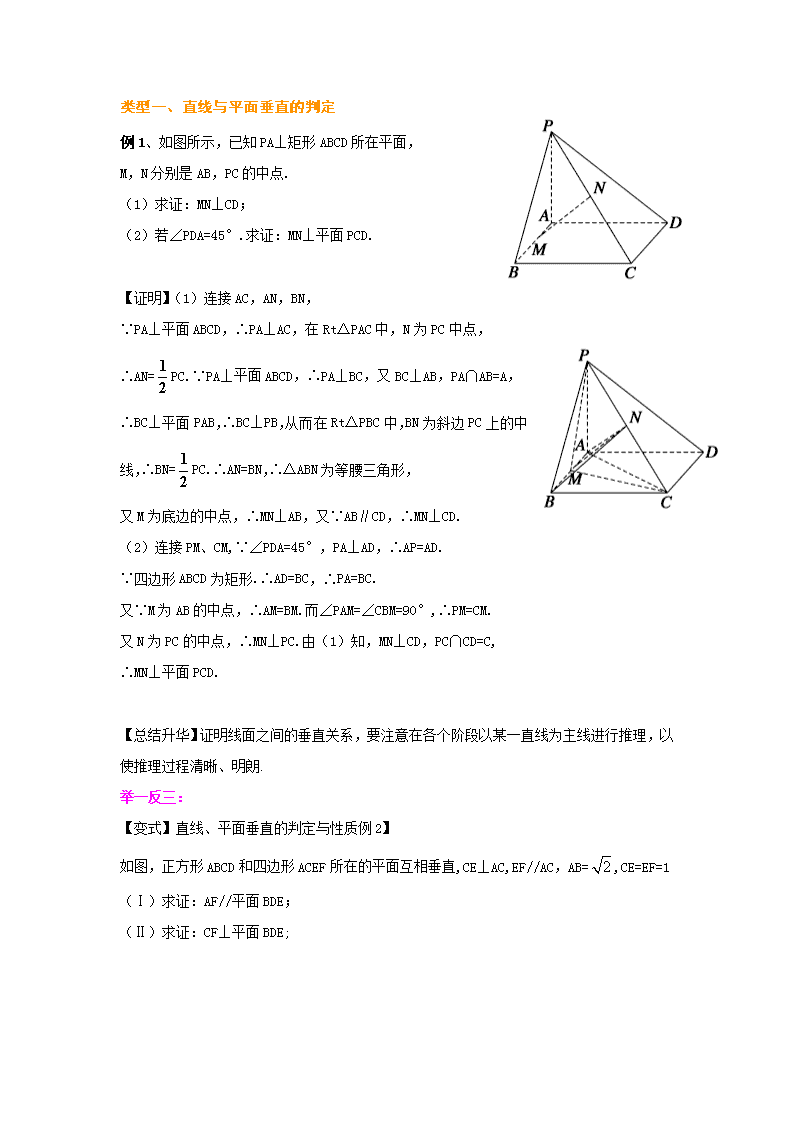‎ ‎【典型例题】‎ 类型一、直线与平面垂直的判定 例1、如图所示，已知PA⊥矩形ABCD所在平面，‎ M，N分别是AB，PC的中点.‎ ‎（1）求证：MN⊥CD；‎ ‎（2）若∠PDA=45°.求证：MN⊥平面PCD.‎ ‎【证明】（1）连接AC，AN，BN，‎ ‎∵PA⊥平面ABCD，∴PA⊥AC，在Rt△PAC中，N为PC中点，‎ ‎∴AN=PC.∵PA⊥平面ABCD，∴PA⊥BC，又BC⊥AB，PA∩AB=A，‎ ‎∴BC⊥平面PAB，∴BC⊥PB，从而在Rt△PBC中，BN为斜边PC上的中线，∴BN=PC.∴AN=BN，∴△ABN为等腰三角形，‎ 又M为底边的中点，∴MN⊥AB，又∵AB∥CD，∴MN⊥CD.‎ ‎（2）连接PM、CM,∵∠PDA=45°，PA⊥AD，∴AP=AD.‎ ‎∵四边形ABCD为矩形.∴AD=BC，∴PA=BC.‎ 又∵M为AB的中点，∴AM=BM.而∠PAM=∠CBM=90°,∴PM=CM.‎ 又N为PC的中点，∴MN⊥PC.由（1）知，MN⊥CD，PC∩CD=C,‎ ‎∴MN⊥平面PCD.‎ ‎【总结升华】证明线面之间的垂直关系，要注意在各个阶段以某一直线为主线进行推理，以使推理过程清晰、明朗.‎ 举一反三：‎ ‎【变式】直线、平面垂直的判定与性质例2】‎ 如图，正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF//AC，AB=,CE=EF=1‎ ‎（Ⅰ）求证：AF//平面BDE；‎ ‎（Ⅱ）求证：CF⊥平面BDE;‎ 证明：（Ⅰ）设AC与BD交于点G。‎ 因为EF∥AG,且EF=1，AG=AC=1，所以四边形AGEF为平行四边形 所以AF∥EG因为EG平面BDE,AF平面BDE,所以AF∥平面BDE ‎（Ⅱ）连接FG，因为EF∥CG,EF=CG=1,且CE=1,所以平行四边形CEFG为菱形 所以CF⊥EG.‎ 因为四边形ABCD为正方形，所以BD⊥AC.‎ 又因为平面ACEF⊥平面ABCD,且平面ACEF∩平面ABCD=AC,‎ 所以BD⊥平面ACEF.所以CF⊥BD.‎ 又BD∩EG=G,所以CF⊥平面BDE.‎ 类型二、直线与平面垂直的性质 例2、如图所示，平面，点C在以AB为直径的⊙O上，，，点E为线段PB的中点，点M在上，且∥．‎ ‎（Ⅰ）求证：平面∥平面PAC；‎ ‎（Ⅱ）求证：平面PAC平面；‎ ‎【解析】‎ ‎（Ⅰ）证明：因为点E为线段PB的中点，点为线段的中点，‎ ‎ 所以 ∥. ‎ ‎ 因为 平面，平面，‎ ‎ 所以 ∥平面PAC. ‎ 因为 ∥，‎ ‎ 因为 平面，平面，‎ ‎ 所以 ∥平面PAC. ‎ 因为 平面，平面，，‎ 所以 平面∥平面PAC. ‎ ‎（Ⅱ）证明：因为 点C在以AB为直径的⊙O上，‎ 所以 ，即. ‎ 因为 平面，平面，‎ 所以 . ‎ 因为 平面，平面，， ‎ 所以 平面.‎ 因为 平面， ‎ 所以 平面PAC平面. ‎ ‎【总结升华】（1）当两个平面垂直时，常作的辅助线是在其中一个面内作交线的垂线。把面面垂直转化为线面垂直，进而可以证明线段线线垂直，构造二面角的平面角或得到点到面的距离相等。‎ ‎（2）已知面面垂直时，通过作辅助线可转化为线面垂直，从而有更多的线线垂直的条件可用，必要时可以通过平面几何的知识证明垂直关系，通过证线面垂直来证线线垂直是空间中两直线垂直证明书的最常用方法。‎ 举一反三：‎ ‎【变式】如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，AB//DC，ΔPAD是等边三角形，已知BD=2AD=8，AB=2DC=4。‎ ‎（1）设M是PC上的一点，证明：平面MBD⊥平面PAD；‎ ‎（2）求四棱锥P-ABCD的体积。‎ ‎【证明】（1）在ΔABD中，‎ ‎（2）过P作PO⊥AD，∵面PAD⊥面ABCD，∴PO⊥面ABCD，即PO为四棱锥P-ABCD的高。又ΔPAD是边长为4的等边三角形，∴PO=。‎ 类型三、平面与平面垂直的判定 例3、如图所示，在三棱锥P—ABC中，PA⊥底面ABC，△ABC为正三角形，D、E分别是BC、CA的中点.‎ ‎（1）证明：平面PBE⊥平面PAC；‎ ‎（2）如何在BC上找一点F，使AD∥平面PEF？并说明理由.‎ ‎【解析】‎ ‎（1）证明 因为PA⊥底面ABC，所以PA⊥BE.‎ 又因为△ABC是正三角形，且E为AC的中点，‎ 所以BE⊥CA.‎ 又PA∩CA=A，所以BE⊥平面PAC. ‎ 因为BE平面PBE，所以平面PBE⊥平面PAC.‎ ‎（2）取CD的中点F，则点F即为所求.‎ 因为E、F分别为CA、CD的中点，所以EF∥AD.‎ 又EF平面PEF，AD平面PEF，‎ 所以AD∥平面PEF.‎ ‎【总结升华】证明线面、面面平行与垂直问题注意要转化为线线的平行与垂直问题。‎ 如图所示，平面ABEF⊥平面ABCD，四边形ABEF与ABCD都是直角梯 ‎ 形，∠BAD=∠FAB=90°,BCAD,BEFA,G、H分别为FA、FD的中点.‎ ‎（1）证明：四边形BCHG是平行四边形；‎ ‎（2）C、D、F、E四点是否共面？为什么？‎ ‎（3）设AB=BE，证明：平面ADE⊥平面CDE.‎ 方法一 (1)证明 由题设知,FG=GA,‎ FH=HD,所以GHAD.‎ 又BCAD,故GHBC.‎ 所以四边形BCHG是平行四边形.‎ ‎(2)解 C、D、F、E四点共面.‎ 理由如下：‎ 由BEAF，G是FA的中点知，‎ BEGF，所以EF∥BG.‎ 由（1）知BG∥CH，所以EF∥CH，故EC、FH共面.‎ 又点D在直线FH上，所以C、D、F、E四点共面.‎ ‎（3）证明 如图，连接EG，由AB=BE，BE AG及∠BAG=90°知ABEG是正方形,故BG⊥EA.‎ 由题设知,FA、AD、AB两两垂直，故AD⊥平面FABE，‎ 因此EA是ED在平面FABE内的射影，根据三垂线定理，BG⊥ED.‎ 又ED∩EA=E,所以BG⊥平面ADE.‎ 由(1)知,CH∥BG,所以CH⊥平面ADE.‎ 由(2)知CH平面CDE,得平面ADE⊥平面CDE.‎ 举一反三：‎ ‎【变式】如图，在四棱锥中，底面是正方形，其他四个侧面都是等边三角形，与的交点为O. ‎ ‎（Ⅰ）求证：平面；‎ O S A B C D E ‎（Ⅱ）已知为侧棱上一个动点. 试问对于上任意一点，平面与平面是否垂直？若垂直，请加以证明；若不垂直，请说明理由.‎ ‎ ‎ ‎【解析】证明：（Ⅰ）因为四边形是正方形，，‎ 所以O是，中点.‎ 由已知，, ,‎ 所以,,‎ 又，‎ 所以平面. ‎ ‎（Ⅱ）对于上任意一点，平面平面.‎ 证明如下：由（Ⅰ）知，‎ 而，所以.‎ 又因为四边形是正方形，所以.‎ 因为，所以.‎ 又因为，所以平面平面. ‎ 类型四、平面与平面垂直的性质及应用 例4如图，在边长为的正三角形中，，，分别为，，上的点，且满足.将△沿折起到△的位置，使平面平面，连结，.（如图）‎ ‎（Ⅰ）若为中点，求证：∥平面；‎ ‎（Ⅱ）求证：.‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 图1 图2 ‎ ‎【解析】‎ 证明：（Ⅰ）取中点，连结．‎ ‎ 在△中，分别为的中点，‎ ‎ 所以∥，且． ‎ ‎ 因为，‎ ‎ 所以∥,且，‎ ‎ 所以∥，且． ‎ ‎ 所以四边形为平行四边形．‎ ‎ 所以∥． ‎ ‎ 又因为平面，且平面，‎ ‎ 所以∥平面． ‎ ‎（Ⅱ） 取中点，连结.‎ 因为，，‎ 所以，而，即△是正三角形. ‎ 又因为, 所以. ‎ 所以在图2中有. ‎ 因为平面平面，平面平面，‎ 所以⊥平面. 又平面，所以⊥. ‎ 举一反三：‎ ‎【变式】如图，四棱锥的底面是边长为的正方形，侧棱底面，且，是侧棱上的动点.‎ ‎(Ⅰ) 求四棱锥的体积；‎ ‎(Ⅱ) 如果是的中点，‎ 求证∥平面；‎ ‎(Ⅲ) 是否不论点在侧棱的任何位置，‎ 都有？证明你的结论．‎ ‎【解析】（Ⅰ） ∵平面，∴‎ 即四棱锥的体积为. ‎ ‎（Ⅱ） 连结交于，连结．‎ ‎∵四边形是正方形，∴是的中点．‎ 又∵是的中点，∴． ‎ 平面平面 ∴平面． ‎ ‎（Ⅲ）不论点在何位置，都有. 　　　 ‎ 证明如下：∵四边形是正方形，∴． ‎ ‎∵底面，且平面，∴． 　 ‎ 又∵，∴平面． 　 ‎ ‎∵不论点在何位置，都有平面. ‎ ‎∴不论点在何位置，都有. ‎