【数学】河南省南阳市六校2019-2020学年高二下学期第二次联考（文）（解析版） 13页

河南省南阳市六校2019-2020学年 高二下学期第二次联考（文）‎ 考生注意：‎ ‎1.本试卷分选择题和非选择题两部分.满分150分，考试时间120分钟.‎ ‎2.答题前，考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚.‎ ‎3.考生作答时，请将答案答在答题卡上.选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效.‎ ‎4.本卷命题范围：北师大版选修1-1（30%），选修1-2（40%），选修4-4（30%）.‎ 一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.命题“，”的否定是（ ）‎ A.， B.，‎ C.， D.， ‎ ‎2.已知，为虚数单位，复数满足，且，则（ ）‎ A.3 B.3或1 C. D.‎ ‎3.圆的圆心的直角坐标为（ ）‎ A. B. C. 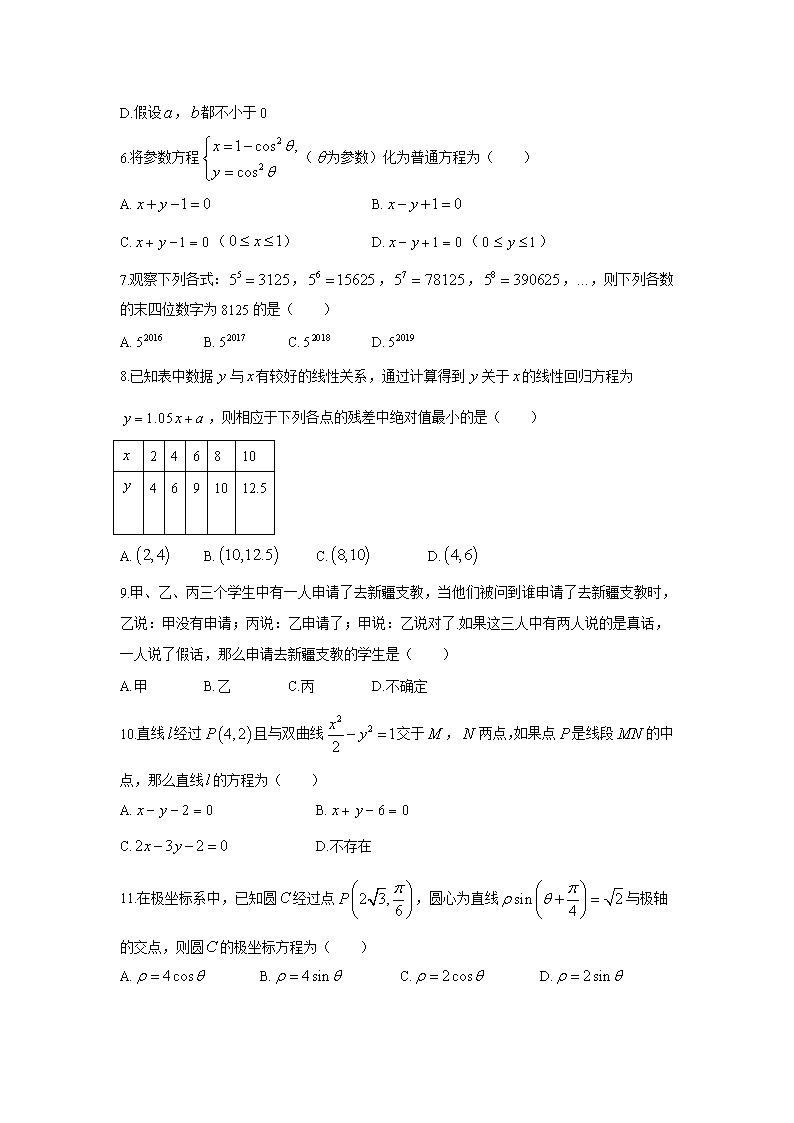D.‎ ‎4.已知椭圆上一点到其一个焦点的距离为3，则点到其另一个焦点的距离等于（ ）‎ A.2 B.3 C.1 D.‎ ‎5.用反证法证明命题“已知，，，则，中至多有一个不小于0”时，假设正确的是（ ）‎ A.假设，都不大于0‎ B.假设，至多有一个大于0‎ C.假设，都小于0‎ D.假设，都不小于0‎ ‎6.将参数方程（为参数）化为普通方程为（ ）‎ A. B.‎ C.（） D.（）‎ ‎7.观察下列各式：，，，，…，则下列各数的末四位数字为8125的是（ ）‎ A. B. C. D.‎ ‎8.已知表中数据与有较好的线性关系，通过计算得到关于的线性回归方程为，则相应于下列各点的残差中绝对值最小的是（ ）‎ ‎2‎ ‎4‎ ‎6‎ ‎8‎ ‎10‎ ‎4‎ ‎6‎ ‎9‎ ‎10‎ ‎12.5‎ A. B. C. D.‎ ‎9.甲、乙、丙三个学生中有一人申请了去新疆支教，当他们被问到谁申请了去新疆支教时，乙说：甲没有申请；丙说：乙申请了；甲说：乙说对了.如果这三人中有两人说的是真话，一人说了假话，那么申请去新疆支教的学生是（ ）‎ A.甲 B.乙 C.丙 D.不确定 ‎10.直线经过且与双曲线交于，两点，如果点是线段的中点，那么直线的方程为（ ）‎ A. B.‎ C. D.不存在 ‎11.在极坐标系中，已知圆经过点，圆心为直线与极轴的交点，则圆的极坐标方程为（ ）‎ A. B. C. D.‎ ‎12.直线与双曲线（，）的左支、右支分别交于，两点，为右焦点，若，则该双曲线的离心率为（ ）‎ A. B. C. 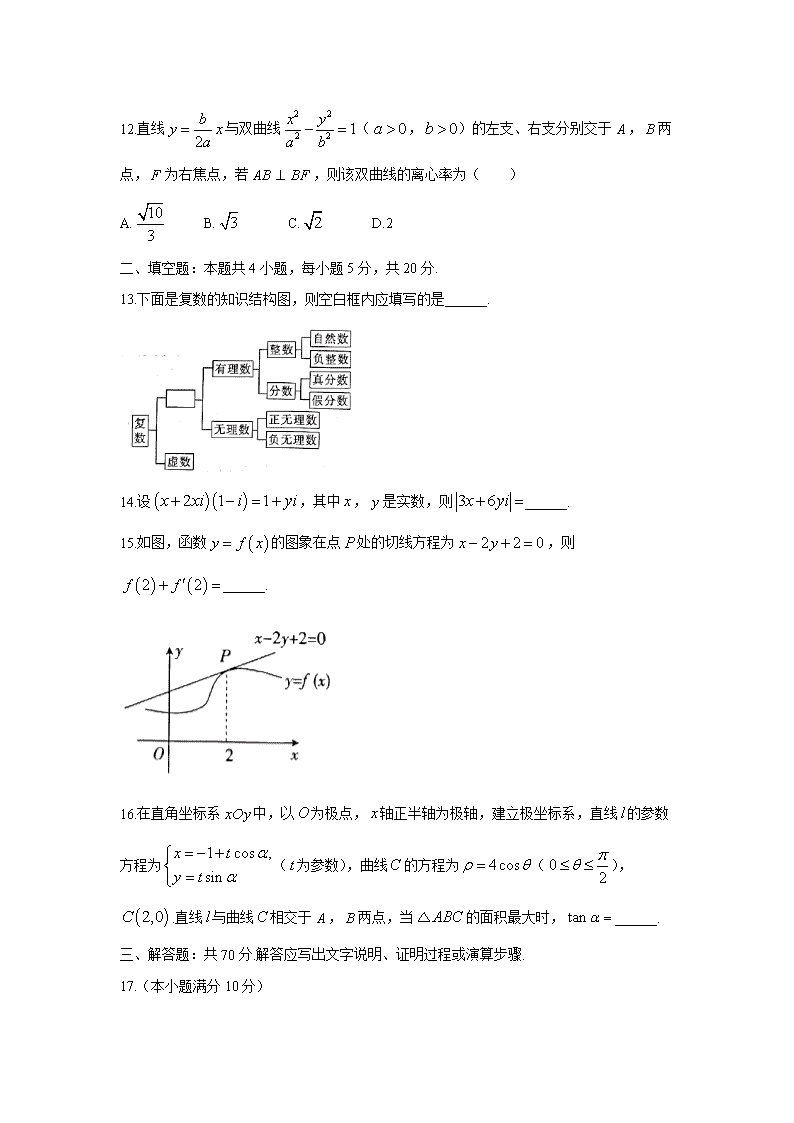D.2‎ 二、填空题：本题共4小题，每小题5分，共20分.‎ ‎13.下面是复数的知识结构图，则空白框内应填写的是______.‎ ‎14.设，其中，是实数，则______.‎ ‎15.如图，函数的图象在点处的切线方程为，则______.‎ ‎16.在直角坐标系中，以为极点，轴正半轴为极轴，建立极坐标系，直线的参数方程为（为参数），曲线的方程为（），.直线与曲线相交于，两点，当的面积最大时，______.‎ 三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.‎ ‎17.（本小题满分10分）‎ ‎2016年1月1日，我国全面实行二孩政策，某机构进行了街头调查，在所有参与调查的青年男女中，持“响应”“犹豫”和“不响应”态度的人数如下表所示：‎ 响应 犹豫 不响应 男性青年 ‎500‎ ‎300‎ ‎200‎ 女性青年 ‎300‎ ‎200‎ ‎300‎ 根据已知条件完成下面的列联表，并判断能否有97.5%的把握认为犹豫与否与性别有关？请说明理由.‎ 犹豫 不犹豫 总计 男性青年 女性青年 总计 ‎1800‎ 参考公式：，.‎ 参考数据：‎ ‎（）‎ ‎0.150‎ ‎0.100‎ ‎0.050‎ ‎0.025‎ ‎0.010‎ ‎2.072‎ ‎2.076‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎18.（本小题满分12分）‎ ‎“双十一网购狂欢节”源于淘宝商城（天猫）2009年11月11日举办的促销活动，当时参与的商家数量和促销力度均有限，但营业额远超预想的效果，于是11月11日成为天猫举办大规模促销活动的固定日期.如今，中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用（单位：万元）和利润（单位：十万元）之间的关系，得到下列数据：‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ ‎9‎ ‎11‎ ‎1‎ ‎2‎ ‎3‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ ‎（1）请用相关系数说明与之间是否存在线性相关关系（当时，说明与之间具有线性相关关系）；‎ ‎（2）根据（1）的判断结果，建立与之间的回归方程，并预测当时，对应的利润为多少（，，精确到0.1）.‎ 附参考公式：回归方程中中和最小二乘估计分别为 ‎，，相关系数 参考数据：‎ ‎，，，.‎ ‎19.（本小题满分12分）‎ 在直角坐标系中，以坐标原点为极点，轴正半轴为极轴建立极坐标系，圆的极坐标方程为.‎ ‎（1）求圆的参数方程；‎ ‎（2）设为圆上一动点，，若点到直线的距离为，求的大小.‎ ‎20.（本小题满分12分）‎ 在直角坐标系中，曲线的参数方程为（为参数）.以直角坐标系的原点为极点，以轴的正半轴为极轴建立极坐标系，已知直线的极坐标方程为.‎ ‎（1）求曲线的普通方程；‎ ‎（2）若与曲线相切，且与坐标轴交于，两点，求以为直径的圆的极坐标方程.‎ ‎21.（本小题满分12分）‎ 在直角坐标系中，曲线：与直线交与，两点.‎ ‎（1）当时，求弦长；‎ ‎（2）轴上是否存在点，使得当变动时，总有？说明理由.‎ ‎22.（本小题满分12分）‎ 已知函数，.‎ ‎（1）当时，求的最值；‎ ‎（2）若函数存在两个极值点，，求的取值范围.‎ 参考答案 ‎1.A 全称命题的否定是特称命题.‎ ‎2.D 因为，所以，又，所以，解得.‎ ‎3.B 圆的直角坐标方程为.‎ ‎4.C ‎5.D 反证法的应用是假设结论不成立，因此要假设为“假设，都不小于0”.‎ ‎6.C 由（为参数），得，但是 ‎7.D 经观察易知的末四位数字为3125，的末四位数字为5625，的末四位数字为8125，的末四位数字为0625，的末四位数字为3125，故周期.由于，因此的末四位数字是8125.故选D.‎ ‎8.B ∵，，∴，∴，∴，相应于点，，，的残差分别为，，，0，故选B.‎ ‎9.C 若乙说了假话，则甲、丙说了真话，那么甲，乙都申请了，与题意只有一人申请矛盾；若丙说了假话，则甲、乙说的话为真，甲.乙都没有申请，申请的人是丙.‎ ‎10.A 当斜率不存在时，显然不符合题意；当斜率存在时，设，代入双曲线方程得，两式相减得，则，则直线方程为，联立直线方程与双曲线方程后，得到，经检验，方程有解，所以直线满足题意.‎ ‎11.A 在中，令，得，‎ 所以圆的圆心坐标为.因为圆经过点，所以圆C的半径 ‎，于是圆过极点，所以圆的极坐标方程为.‎ ‎12.B 联立与，得，∴，∴，‎ 则，∵，∴，‎ 整理得，即，∴.‎ ‎13.实数 复数包括实数与虚数.‎ ‎14. 由，化简得，即解得 ‎∴.‎ ‎15. 由图可知，，将代入，得，∴过，即，∴.‎ ‎16. 曲线的普通方程为（），表示的是以为圆心，2为半径的上半个圆.由题意可知，当为直角时的面积最大，此时到直线的距离，因为直线与轴交于，所以，于是，所以.‎ ‎17.解：完成列联表如下 犹豫 不犹豫 总计 男性青年 ‎300‎ ‎700‎ ‎1000‎ 女性青年 ‎200‎ ‎600‎ ‎800‎ 总计 ‎500‎ ‎1300‎ ‎1800‎ ‎……………………5分 因为，………………8分 所以有97.5%的把握认为犹豫与否与性别有关.……………………10分 ‎18.解：（1）由题意得，.……………………2分 又，，，‎ 所以，‎ ‎…………5分 所以，与之间具有线性相关关系.………………6分 ‎（2）因为，……………………8分 ‎，‎ 所以回归直线方程为.………………10分 当时，.………………12分 ‎19.解：（1）∵，∴，∴，………………2分 即，∴圆的参数方程为（为参数）.………………5分 ‎（2）由（1）可设，，………………6分 的直角坐标方程为，………………7分 则到直线的距离为 ‎，…………9分 ‎∴，‎ ‎∵，∴或，‎ 故或.………………12分 ‎20.解：（1）由，得，………………1分 ‎，即，‎ 故曲线的普通方程为.………………4分 ‎（2）由，得，…………5分 联立，得，………………6分 因为与曲线相切，所以，.………………7分 所以的方程为，不妨假设，则，线段的中点为.…………8分 所以，又，‎ 故以为直径的圆的直角坐标方程为，………………10分 其对应的极坐标方程为.………………12分 ‎21.解：（1）当时，直线方程为，设，，‎ 联立∴，………………2分 ‎∴，，‎ ‎∴.………………5分 ‎（2）假设存在满足条件的点，设，，，‎ 联立∴，‎ 则，∴，.………………7分 ‎∵，∴，‎ 即.………………8分 所以，整理得：，‎ 所以，所以对任意成立，所以，‎ 所以存在点满足要求.………………12分 ‎22.解：（1）当时，，‎ ‎，…………1分 令，得，‎ 所以函数在上单调递减，在上单调递增，…………2分 所以当时，，无最大值.………………4分 ‎（2）（），‎ ‎，……………………5分 由题知，，是方程的两个不相等的正实数根，‎ 即，是方程的两个不相等的正实数根，…………6分 所以 解得.………………8分 因为 是关于的减函数，………………11分 所以.‎ 故的取值范围是.………………12分