【数学】2019届一轮复习人教A版（文）第八章第七节抛物线学案 26页

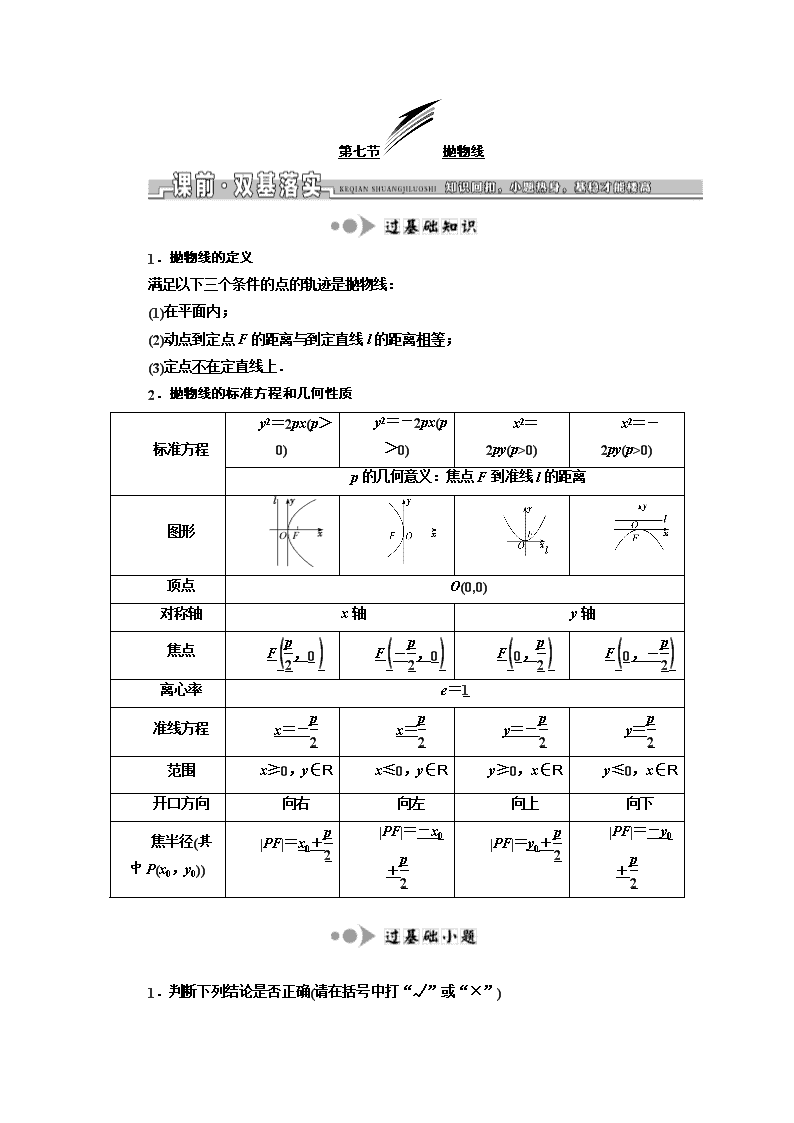
第七节抛物线 ‎1．抛物线的定义 满足以下三个条件的点的轨迹是抛物线：‎ ‎(1)在平面内；‎ ‎(2)动点到定点F的距离与到定直线l的距离相等；‎ ‎(3)定点不在定直线上．‎ ‎2．抛物线的标准方程和几何性质 标准方程 y2＝2px(p＞0)‎ y2＝－2px(p＞0)‎ x2＝2py(p>0)‎ x2＝－2py(p>0)‎ p的几何意义：焦点F到准线l的距离 图形 顶点 O(0,0)‎ 对称轴 x轴 y轴 焦点 F F F F 离心率 e＝ 准线方程 x＝－ x＝ y＝－ y＝ 范围 x≥0，y∈R x≤0，y∈R y≥0，x∈R y≤0，x∈R 开口方向 向右 向左 向上 向下 焦半径(其中P(x0，y0))‎ ‎|PF|＝x0＋ ‎|PF|＝－x0＋ ‎|PF|＝y0＋ ‎|PF|＝－y0＋ ‎1．判断下列结论是否正确(请在括号中打“√”或“×”)‎ ‎(1)平面内与一个定点F和一条定直线l的距离相等的点的轨迹一定是抛物线．(　　)‎ ‎(2)抛物线y2＝4x的焦点到准线的距离是4.(　　)‎ ‎(3)抛物线既是中心对称图形，又是轴对称图形．(　　)‎ ‎(4)方程y＝ax2(a≠0)表示的曲线是焦点在x轴上的抛物线，且其焦点坐标是，准线方程是x＝－.(　　)‎ 答案：(1)×　(2)×　(3)×　(4)×‎ ‎2．已知点F，直线l：x＝－，点B是l上的动点．若过点B垂直于y轴的直线与线段BF的垂直平分线交于点M，则点M的轨迹是(　　)‎ A．双曲线　　　　　　　 　B．椭圆 C．圆 D．抛物线 解析：选D　由已知得|MF|＝|MB|，根据抛物线的定义知，点M的轨迹是以点F为焦点，直线l为准线的抛物线．‎ ‎3．抛物线8x2＋y＝0的焦点坐标为________．‎ 解析：由8x2＋y＝0，得x2＝－y.‎ ‎∴2p＝，p＝，‎ ‎∴焦点为.‎ 答案： ‎4．焦点在直线2x＋y＋2＝0上的抛物线的标准方程为________．‎ 解析：当焦点在x轴上时，令方程2x＋y＋2＝0中的y＝0，得焦点为(－1,0)，‎ 故抛物线方程为y2＝－4x，‎ 当焦点在y轴上时，令方程2x＋y＋2＝0中的x＝0，得焦点为(0，－2)，‎ 故抛物线方程为x2＝－8y.‎ 答案：y2＝－4x或x2＝－8y ‎5．(教材习题改编)若抛物线y＝4x2上的一点M到焦点的距离为1，则点M的纵坐标是________．‎ 解析：M到准线的距离等于M到焦点的距离，‎ 又准线方程为y＝－，‎ 设M(x，y)，则y＋＝1，∴y＝.‎ 答案： 　　　　 ‎[考什么·怎么考]‎ 高考要求考生掌握四种不同的抛物线的标准形式.高考试题的考查形式主要有两种：一是求抛物线的方程；二是根据抛物线的方程研究抛物线的几何性质，题型多为选择题、填空题，难度适中.‎ ‎1．顶点在原点，对称轴为坐标轴，且过点P(－4，－2)的抛物线的标准方程是(　　)‎ A．y2＝－x　　　　　　　　 　B．x2＝－8y C．y2＝－8x或x2＝－y D．y2＝－x或x2＝－8y 解析：选D　(待定系数法)设抛物线为y2＝mx，代入点P(－4，－2)，解得m＝－1，则抛物线方程为y2＝－x；设抛物线为x2＝ny，代入点P(－4，－2)，解得n＝－8，则抛物线方程为x2＝－8y.‎ ‎2．已知抛物线y2＝2px(p＞0)的准线经过点(－1,1)，则该抛物线的焦点坐标为(　　)‎ A．(－1,0) B．(1,0)‎ C．(0，－1) D．(0,1)‎ 解析：选B　抛物线y2＝2px(p＞0)的准线方程为x＝－，由题设知－＝－1，即＝1，所以焦点坐标为(1,0)．‎ ‎3．若抛物线的顶点在原点，开口向上，F为焦点，M为准线与y轴的交点，A为抛物线上一点，且|AM|＝，|AF|＝3，则此抛物线的标准方程为________________．‎ 解析：设所求抛物线的标准方程为x2＝2py(p＞0)，A(x1，y1)，则F，M，‎ 则解得p＝4或p＝2.‎ 故所求抛物线的标准方程为x2＝8y或x2＝4y.‎ 答案：x2＝8y或x2＝4y ‎4．(2017·天津高考)设抛物线y2＝4x的焦点为F，准线为l.已知点C在l上，以C为圆心的圆与y轴的正半轴相切于点A.若∠FAC＝120°，则圆的方程为________________．‎ 解析：由题意知该圆的半径为1，‎ 设圆心坐标为C(－1，a)(a＞0)，则A(0，a)．‎ 又F(1,0)，所以＝(－1,0)，＝(1，－a)，‎ 由题意得与的夹角为120°，‎ 故cos 120°＝＝－，解得a＝，‎ 所以圆的方程为(x＋1)2＋(y－)2＝1.‎ 答案：(x＋1)2＋(y－)2＝1‎ ‎[怎样快解·准解]‎ 求抛物线标准方程的方法 ‎(1)抛物线的标准方程有四种不同的形式，要掌握焦点到准线的距离，顶点到准线、焦点的距离，通径长与标准方程中系数2p的关系．‎ ‎(2)求标准方程要先确定形式，必要时要进行分类讨论，标准方程有时可设为y2＝mx或x2＝my(m≠0)．‎ ‎(3)焦点到准线的距离简称为焦准距，抛物线y2＝2px(p＞0)上的点常设为.‎ ‎[注意]　求抛物线的标准方程时，一定要先确定抛物线的焦点坐标，即抛物线标准方程的形式，否则极易发生漏解的情况．(如第1题)‎ 　　　　 ‎[题点全练]‎ 角度(一)　利用抛物线的定义解决最值、距离问题 ‎1．若点A的坐标为(3,2)，F是抛物线y2＝2x的焦点，点M在抛物线上移动时，使|MF|＋|MA|取得最小值的M的坐标为(　　)‎ A．(0,0)　　　　　　　　 　B. C．(1，) D．(2,2)‎ 解析：选D　过点M作准线的垂线，垂足是N，则|MF|＋|MA|＝|MN|＋|MA|，当A，M，N三点共线时，|MF|＋|MA|取得最小值，此时M(2,2)．‎ ‎2．已知直线l1：4x－3y＋6＝0和直线l2：x＝－1，抛物线y2＝4x上一动点P到直线l1‎ 和直线l2的距离之和的最小值是(　　)‎ A. B．2‎ C. D．3‎ 解析：选B　由题可知l2：x＝－1是抛物线y2＝4x的准线，设抛物线的焦点为F(1,0)，则动点P到l2的距离等于|PF|，故动点P到直线l1和直线l2的距离之和的最小值，即焦点F到直线l1：4x－3y＋6＝0的距离，所以最小值是＝2.‎ ‎3．(2017·全国卷Ⅱ)过抛物线C：y2＝4x的焦点F，且斜率为的直线交C于点M(M在x轴的上方)，l为C的准线，点N在l上且MN⊥l，则M到直线NF的距离为(　　)‎ A. B．2 C．2 D．3 解析：选C　法一：由题意，得F(1,0)，‎ 则直线FM的方程是y＝(x－1)．‎ 由得x＝或x＝3.‎ 由M在x轴的上方，得M(3,2)，‎ 由MN⊥l，得|MN|＝|MF|＝3＋1＝4.‎ 又∠NMF等于直线FM的倾斜角，即∠NMF＝60°，‎ 因此△MNF是边长为4的等边三角形，‎ 所以点M到直线NF的距离为4×＝2.‎ 法二：依题意，得直线FM的倾斜角为60°，‎ 则|MN|＝|MF|＝＝4.‎ 又∠NMF等于直线FM的倾斜角，即∠NMF＝60°，‎ 因此△MNF是边长为4的等边三角形，‎ 所以点M到直线NF的距离为4×＝2.‎ ‎[题型技法]‎ ‎(1)涉及抛物线的焦点和准线的有关问题，应充分利用抛物线的定义求解．由抛物线定义，把抛物线上点到焦点距离与到准线距离相互转化．‎ ‎(2)注意灵活运用抛物线上一点P(x，y)到焦点F的距离|PF|＝|x|＋或|PF|＝|y|＋.‎ 角度(二)　利用抛物线的定义处理焦点弦问题 ‎4．(2017·全国卷Ⅰ)已知F为抛物线C：y2＝4x的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于A，B两点，直线l2与C交于D，E两点，则|AB|＋|DE|的最小值为(　　)‎ A．16 B．14‎ C．12 D．10‎ ‎[思维路径]‎ 要求|AB|＋|DE|的最小值，需用合适的变量表示|AB|＋|DE|，因为AB和DE均过焦点F，故考虑利用抛物线的定义，用点A，B和D，E的坐标表示|AB|和|DE|，然后利用函数或基本不等式求最值．‎ 解析：选A　法一：抛物线C：y2＝4x的焦点为F(1,0)，‎ 由题意可知l1，l2的斜率存在且不为0.‎ 不妨设直线l1的斜率为k，‎ 则l1：y＝k(x－1)，l2：y＝－(x－1)，‎ 由消去y，得k2x2－(2k2＋4)x＋k2＝0，‎ 设A(x1，y1)，B(x2，y2)，‎ ‎∴x1＋x2＝＝2＋，‎ 由抛物线的定义可知，‎ ‎|AB|＝x1＋x2＋2＝2＋＋2＝4＋.‎ 同理得|DE|＝4＋4k2，‎ ‎∴|AB|＋|DE|＝4＋＋4＋4k2‎ ‎＝8＋4≥8＋8＝16，‎ 当且仅当＝k2，即k＝±1时取等号，‎ 故|AB|＋|DE|的最小值为16.‎ 法二：如图所示，设直线AB的倾斜角为θ，过A，B分别作准线的垂线，垂足为A1，B1，‎ 则|AF|＝|AA1|，|BF|＝|BB1|，过点F向AA1引垂线FG，得＝＝cos θ，‎ 则|AF|＝，同理|BF|＝，‎ 则|AB|＝|AF|＋|BF|＝，即|AB|＝，‎ 因为l1与l2垂直，故直线DE的倾斜角为θ＋或θ－，‎ 则|DE|＝，则|AB|＋|DE|＝＋ ‎＝＝＝，‎ 则易知|AB|＋|DE|的最小值为16.‎ ‎[题型技法]‎ ‎1．灵活选用方法准解题 定义法 ‎|AB|＝x1＋x2＋p 斜率法 ‎|AB|＝×2p(k为AB的斜率)‎ 倾斜角法 ‎|AB|＝(θ为AB的倾斜角)‎ ‎2．谨记二级结论快解题 如图所示，AB是抛物线y2＝2px(p＞0)过焦点F的一条弦，设A(x1，y1)，B(x2，y2)．‎ ‎①y1y2＝－p2，x1x2＝.‎ ‎②|AF|＝，|BF|＝(θ为AB的倾斜角)．‎ ‎③＋为定值.‎ ‎④焦点弦端点与顶点构成的三角形面积：‎ S△AOB＝＝|AB||d|＝|OF|·|y1－y2|.‎ ‎⑤以AB为直径的圆与准线相切．‎ ‎⑥以AF或BF为直径的圆与y轴相切．‎ ‎⑦过焦点弦的端点的切线互相垂直且交点在准线上．‎ ‎[冲关演练]‎ ‎1．(2017·全国卷Ⅱ)已知F是抛物线C：y2＝8x的焦点，M是C上一点，FM的延长线交y轴于点N.若M为FN的中点，则|FN|＝________.‎ 解析：法一：依题意，抛物线C：y2＝8x的焦点F(2,0)，因为M是C上一点，FM的延长线交y轴于点N，M为FN的中点，设M(a，b)(b>0)，所以a＝1，b＝2，所以N(0,4)，|FN|＝＝6.‎ 法二：如图，不妨设点M位于第一象限内，抛物线C的准线交x轴于点A，过点M作准线的垂线，垂足为点B，交y轴于点P，∴PM∥OF.由题意知，F(2，0)，|FO|＝|AO|＝2.‎ ‎∵点M为FN的中点，PM∥OF，‎ ‎∴|MP|＝|FO|＝1.‎ 又|BP|＝|AO|＝2，‎ ‎∴|MB|＝|MP|＋|BP|＝3.‎ 由抛物线的定义知|MF|＝|MB|＝3，‎ 故|FN|＝2|MF|＝6.‎ 答案：6‎ ‎2．已知过抛物线y2＝2px(p>0)的焦点，斜率为2的直线交抛物线于A(x1，y1)，B(x2，y2)(x10)的焦点为F，经过点F的直线交抛物线于A，B两点，点C 在抛物线的准线上，且BC∥x轴．证明：直线AC经过原点O.‎ 证明：设直线AB的方程为x＝my＋，‎ 代入y2＝2px，得y2－2pmy－p2＝0.‎ 由根与系数的关系，得yAyB＝－p2，即yB＝－.‎ ‎∵BC∥x轴，且C在准线x＝－上，‎ ‎∴C.‎ 则kOC＝＝＝＝kOA.‎ ‎∴直线AC经过原点O.‎ 　　　　 直线与抛物线的位置关系是每年高考的重点，题型既有选择题、填空题，也有解答题，属于中等偏上.‎ ‎[典题领悟]‎ ‎(2017·全国卷Ⅰ)设A，B为曲线C：y＝上两点，A与B的横坐标之和为4.‎ ‎(1)求直线AB的斜率；‎ ‎(2)设M为曲线C上一点，C在M处的切线与直线AB平行，且AM⊥BM，求直线AB的方程．‎ ‎[学审题]‎ 看到曲线的切线?想到导数的几何意义；看到AM⊥BM?想到直角三角形的性质或·＝0.‎ 解：(1)设A(x1，y1)，B(x2，y2)，‎ 则x1≠x2，y1＝，y2＝，x1＋x2＝4，‎ 于是直线AB的斜率k＝＝＝1.‎ ‎(2)法一：由y＝，得y′＝.‎ 设M(x3，y3)，由题设知＝1，解得x3＝2，‎ 于是M(2,1)．‎ 设直线AB的方程为y＝x＋m，‎ 故线段AB的中点为N(2,2＋m)，|MN|＝|m＋1|.‎ 将y＝x＋m代入y＝，得x2－4x－‎4m＝0.‎ 当Δ＝16(m＋1)＞0，即m＞－1时，x1,2＝2±2.‎ 从而|AB|＝|x1－x2|＝4.‎ 由题设知|AB|＝2|MN|，‎ 即4＝2(m＋1)，解得m＝7.‎ 所以直线AB的方程为x－y＋7＝0.‎ 法二：由y＝，得y′＝，‎ 设M(x3，y3)，由题设知＝1，‎ 解得x3＝2，于是M(2,1)．‎ 设直线AB的方程为y＝x＋m，‎ 由得x2－4x－‎4m＝0.‎ 由Δ＝16(m＋1)＞0，得m＞－1.‎ 则x1＋x2＝4，x1x2＝－‎4m.‎ ‎∵AM⊥BM，∴·＝0，‎ 即(x1－2)(x2－2)＋(y1－1)(y2－1)＝0，‎ 又y＝x＋m，‎ ‎∴(x1－2)(x2－2)＋(x1＋m－1)(x2＋m－1)＝0，‎ 即2x1x2＋(m－3)(x1＋x2)＋4＋(m－1)2＝0，‎ ‎∴－‎8m＋4(m－3)＋4＋(m－1)2＝0，‎ 整理得m2－‎6m－7＝0，‎ 解得m＝7或m＝－1，‎ 又m＞－1，∴m＝7，‎ ‎∴直线AB的方程为x－y＋7＝0.‎ ‎[解题师说]‎ 解决直线与抛物线的位置关系问题的常用方法 ‎(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系．‎ ‎(2)有关直线与抛物线相交的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式|AB|＝|xA|＋|xB|＋p或|AB|＝|yA|＋|yB|＋p，若不过焦点，则必须用一般弦长公式．‎ ‎(3)涉及抛物线的弦长、中点、距离等相关问题时，一般利用根与系数的关系采用“设而不求”“整体代入”等解法．‎ ‎[注意]　涉及弦的中点、斜率时一般用“点差法”求解．‎ ‎[冲关演练]‎ ‎(2018·洛阳模拟)已知抛物线C：x2＝2py(p＞0)，过焦点F的直线交C于A，B两点，D是抛物线的准线l与y轴的交点．‎ ‎(1)若AB∥l，且△ABD的面积为1，求抛物线的方程；‎ ‎(2)设M为AB的中点，过M作l的垂线，垂足为N.证明：直线AN与抛物线相切．‎ 解：(1)∵AB∥l，∴|FD|＝p，|AB|＝2p.‎ ‎∴S△ABD＝p2，∴p＝1，‎ 故抛物线C的方程为x2＝2y.‎ ‎(2)设直线AB的方程为y＝kx＋，‎ 由得x2－2kpx－p2＝0.‎ ‎∴x1＋x2＝2kp，x1x2＝－p2.‎ 其中A，B.‎ ‎∴M，N.‎ ‎∴kAN＝＝＝＝＝.‎ 又x2＝2py，∴y′＝.‎ ‎∴抛物线x2＝2py在点A处的切线斜率k＝.‎ ‎∴直线AN与抛物线相切．‎ ‎(一)普通高中适用作业 A级——基础小题练熟练快 ‎1．已知抛物线x2＝2py(p＞0)的准线经过点(1，－1)，则抛物线的焦点坐标为(　　)‎ A．(0,1)　　　　　　　　 　B．(0,2)‎ C．(1,0) D．(2,0)‎ 解析：选A　由抛物线x2＝2py(p＞0)的准线为y＝－＝－1，得p＝2，故所求抛物线的焦点坐标为(0,1)．‎ ‎2．已知AB是抛物线y2＝2x的一条焦点弦，|AB|＝4，则AB中点C的横坐标是(　　)‎ A．2 B. C. D. 解析：选C　设A(x1，y1)，B(x2，y2)，则|AB|＝x1＋x2＋p＝4，又p＝1，所以x1＋x2＝3，所以点C的横坐标是＝.‎ ‎3．设抛物线C：y2＝4x的焦点为F，准线l与x轴的交点为A，过抛物线C上一点P作准线l的垂线，垂足为Q.若△QAF的面积为2，则点P的坐标为(　　)‎ A．(1,2)或(1，－2) B．(1,4)或(1，－4)‎ C．(1,2) D．(1,4)‎ 解析：选A　设点P的坐标为(x0，y0)．因为△QAF的面积为2，所以×2×|y0|＝2，即|y0|＝2，所以x0＝1，所以点P的坐标为(1,2)或(1，－2)．‎ ‎4．已知点F是抛物线y2＝x的焦点，A，B是该抛物线上的两点．若|AF|＋|BF|＝3，则线段AB的中点到y轴的距离为(　　)‎ A. B. C. D．1‎ 解析：选B　设A(xA，yA)，B(xB，yB)，则|AF|＋|BF|＝xA＋＋xB＋＝xA＋xB＋p＝3，则AB的中点C到y轴的距离d＝＝＝.‎ ‎5．已知点A(0,2)，抛物线C1：y2＝ax(a＞0)的焦点为F，射线FA与抛物线C相交于点M，与其准线相交于点N.若|FM|∶|MN|＝1∶，则a的值为(　　)‎ A. B. C．1 D．4‎ 解析：选D　依题意，点F的坐标为，设点M在准线上的射影为K，由抛物线的定义知|MF|＝|MK|，|KM|∶|MN|＝1∶，则|KN|∶|KM|＝2‎ ‎∶1.∵kFN＝＝－，kFN＝－＝－2，∴＝2，解得a＝4.‎ ‎6．已知抛物线y2＝4x的焦点为F，过焦点F的直线交抛物线于A，B两点，O为坐标原点．若△AOB的面积为4，则|AB|＝(　　)‎ A．6 B．8‎ C．12 D．16‎ 解析：选D　设A，B，F(1,0)．当AB⊥x轴时，|AB|＝4，S△AOB＝|OF|·|AB|＝2，不成立，所以＝⇒y1y2＝－4.由△AOB的面积为4，得|y1－y2|×1＝4，所以y＋y＝56，因此|AB|＝x1＋x2＋p＝＋2＝16.‎ ‎7．已知点P在抛物线y2＝4x上，且点P到y轴的距离与其到焦点的距离之比为，则点P到x轴的距离为________．‎ 解析：设点P的坐标为(xP，yP)，抛物线y2＝4x的准线方程为x＝－1，根据抛物线的定义，点P到焦点的距离等于点P到准线的距离，故＝，‎ 解得xP＝1，‎ 所以y＝4，所以|yP|＝2.‎ 答案：2‎ ‎8．一个顶点在原点，另外两点在抛物线y2＝2x上的正三角形的面积为________．‎ 解析：如图，根据抛物线的对称性得∠AOx＝30°.‎ 直线OA的方程y＝x，‎ 代入y2＝2x，得x2－6x＝0，‎ 解得x＝0或x＝6.‎ 即得A的坐标为(6,2)．‎ ‎∴|AB|＝4，正三角形OAB的面积为×4×6＝12.‎ 答案：12 ‎9．已知抛物线y2＝4x，过焦点F的直线与抛物线交于A，B两点，过A，B分别作y轴的垂线，垂足分别为C，D，则|AC|＋|BD|的最小值为________．‎ 解析：由题意知F(1,0)，|AC|＋|BD|＝|AF|＋|FB|－2＝|AB|－2，即|AC|＋|BD|取得最小值时当且仅当|AB|取得最小值．依抛物线定义知当|AB|为通径，即|AB|＝2p＝4‎ 时为最小值，所以|AC|＋|BD|的最小值为2.‎ 答案：2‎ ‎10．已知抛物线y2＝4x的焦点为F，过点F作一条直线交抛物线于A，B两点．若|AF|＝3，则|BF|＝________.‎ 解析：设A(xA，yA)，B(xB，yB)，点A在第一象限，‎ 则|AF|＝xA＋1＝3，所以xA＝2，yA＝2，‎ 所以直线AB的斜率为k＝＝2.‎ 则直线AB的方程为y＝2(x－1)，‎ 与抛物线方程联立整理得2x2－5x＋2＝0，xA＋xB＝，‎ 所以xB＝，所以|BF|＝xB＋＝＋1＝.‎ 答案： B级——中档题目练通抓牢 ‎1．已知抛物线C：y2＝8x的焦点为F，P是抛物线C的准线上一点，且P的纵坐标为正数，Q是直线PF与抛物线C的一个交点．若|PQ|＝|QF|，则直线PF的方程为(　　)‎ A．x－y－2＝0 B．x＋y－2＝0‎ C．x－y＋2＝0 D．x＋y＋2＝0‎ 解析：选B　如图，过点Q作QM⊥l于点M.∵|QF|等于点Q到准线的距离|QM|，∴|PQ|＝|QM|，∴∠PQM＝45°，∴∠PFO＝45°，∴直线PF的倾斜角为135°，即斜率k＝－1，∴直线PF的方程为y－0＝－1×(x－2)，即x＋y－2＝0.‎ ‎2．已知点P是抛物线y2＝2x上的动点，点P在y轴上的射影是M，点A，则|PA|＋|PM|的最小值是(　　)‎ A. B．4‎ C. D．5‎ 解析：选C　设抛物线y2＝2x的焦点为F，‎ 则|PF|＝|PM|＋，∴|PM|＝|PF|－.‎ ‎∴|PA|＋|PM|＝|PA|＋|PF|－.‎ 将x＝代入抛物线方程y2＝2x，得y＝±.‎ ‎∵＜4，∴点A在抛物线的外部．‎ ‎∴当P，A，F三点共线时，|PA|＋|PF|有最小值．‎ ‎∵F，∴|AF|＝ ＝5.‎ ‎∴|PA|＋|PM|有最小值5－＝.‎ ‎3.如图，过抛物线y2＝2px(p>0)的焦点F的直线依次交抛物线及其准线于点A，B，C，若|BC|＝2|BF|，且|AF|＝3，则抛物线的方程为(　　)‎ A．y2＝x　　　　　 　B．y2＝3x C．y2＝x D．y2＝9x 解析：选B　如图，分别过点A，B作准线的垂线，交准线于点E，D，‎ 设|BF|＝a，则|BC|＝‎2a，‎ 由抛物线的定义得，|BD|＝a，‎ 故∠BCD＝30°，‎ 在直角三角形ACE中，‎ 因为|AE|＝|AF|＝3，|AC|＝3＋‎3a，‎ ‎2|AE|＝|AC|，‎ 所以6＝3＋‎3a，从而得a＝1，‎ 因为BD∥FG，所以＝.‎ 即＝，解得p＝，‎ 因此抛物线方程为y2＝3x.‎ ‎4．(2017·山东高考)在平面直角坐标系xOy中，双曲线－＝1(a>0，b>0)的右支与焦点为F的抛物线x2＝2py(p>0)交于A，B两点．若|AF|＋|BF|＝4|OF|，则该双曲线的渐近线方程为________．‎ 解析：设A(x1，y1)，B(x2，y2)，由抛物线的定义可知 ‎|AF|＝y1＋，|BF|＝y2＋，|OF|＝，‎ 由|AF|＋|BF|＝y1＋＋y2＋＝y1＋y2＋p＝4|OF|＝2p，得y1＋y2＝p.‎ 联立消去x，得a2y2－2pb2y＋a2b2＝0，‎ 所以y1＋y2＝，所以＝p，‎ 即＝，故＝，‎ 所以双曲线的渐近线方程为y＝±x.‎ 答案：y＝±x ‎5．已知直线y＝a交抛物线y＝x2于A，B两点．若该抛物线上存在点C，使得∠ACB为直角，则实数a的取值范围为________．‎ 解析：如图，设C(x0，x)(x≠a)，A(－，a)，B(，a)，‎ 则＝(－－x0，a－x)，＝(－x0，a－x)．‎ ‎∵CA⊥CB，∴·＝0，‎ 即－(a－x)＋(a－x)2＝0，(a－x)(－1＋a－x)＝0.‎ ‎∴x＝a－1≥0，∴a≥1.‎ 答案：[1，＋∞)‎ ‎6．已知抛物线y2＝2px(p>0)的焦点为F，A是抛物线上横坐标为4，且位于x轴上方的点，A到抛物线准线的距离等于5，过A作AB垂直于y轴，垂足为B，OB的中点为M.‎ ‎(1)求抛物线的方程；‎ ‎(2)若过M作MN⊥FA，垂足为N，求点N的坐标．‎ 解：(1)抛物线y2＝2px的准线为x＝－，‎ 于是4＋＝5，∴p＝2.‎ ‎∴抛物线方程为y2＝4x.‎ ‎(2)∵点A的坐标是(4,4)，‎ 由题意得B(0,4)，M(0,2)．‎ 又∵F(1,0)，∴kFA＝，‎ ‎∵MN⊥FA，∴kMN＝－.‎ ‎∴FA的方程为y＝(x－1)，①‎ MN的方程为y－2＝－x，②‎ 联立①②，解得x＝，y＝，‎ ‎∴N的坐标为.‎ ‎7.如图所示，抛物线关于x轴对称，它的顶点在坐标原点，点P(1,2)，A(x1，y1)，B(x2，y2)均在抛物线上．‎ ‎(1)写出该抛物线的方程及其准线方程．‎ ‎(2)当PA与PB的斜率存在且倾斜角互补时，求y1＋y2的值及直线AB的斜率．‎ 解：(1)由已知条件，可设抛物线的方程为y2＝2px(p>0)．‎ 因为点P(1,2)在抛物线上，‎ 所以22＝2p×1，解得p＝2.‎ 故所求抛物线的方程是y2＝4x，准线方程是x＝－1.‎ ‎(2)设直线PA的斜率为kPA，直线PB的斜率为kPB.‎ 则kPA＝(x1≠1)，kPB＝(x2≠1)，‎ 因为PA与PB的斜率存在且倾斜角互补，‎ 所以kPA＝－kPB.‎ 由A(x1，y1)，B(x2，y2)均在抛物线上，‎ 得 所以＝－，‎ 所以y1＋2＝－(y2＋2)．‎ 所以y1＋y2＝－4.‎ 由①－②得，y－y＝4(x1－x2)，‎ 所以kAB＝＝＝－1(x1≠x2)．‎ C级——重难题目自主选做 ‎1．过抛物线y2＝4x的焦点F的直线交抛物线于A，B两点，分别过A，B两点作准线的垂线，垂足分别为A′，B′两点，以线段A′B′为直径的圆C过点E(－2,3)，则圆C的方程为(　　)‎ A．(x＋1)2＋(y－2)2＝2‎ B．(x＋1)2＋(y－1)2＝5‎ C．(x＋1)2＋(y＋1)2＝17‎ D．(x＋1)2＋(y＋2)2＝26‎ 解析：选B　设直线AB的方程为x－1＝ty.‎ 由得y2－4ty－4＝0.‎ 设A(x1，y1)，B(x2，y2)，则A′(－1，y1)，B′(－1，y2)．‎ ‎∴y1＋y2＝4t，y1y2＝－4.‎ 又∵以A′B′为直径的圆C过点E(－2,3)，‎ ＝(－1,3－y1)，＝(－1,3－y2)，‎ ‎∴·＝1＋(3－y1)(3－y2)＝0，‎ 即y1y2－3(y1＋y2)＋10＝－4－12t＋10＝0，解得t＝.‎ ‎∴y1＋y2＝2，‎ ‎∴圆C的圆心为＝(－1,1)．‎ 半径R＝＝＝.‎ ‎∴圆C的方程为(x＋1)2＋(y－1)2＝5.‎ ‎2．(2018·武汉调研)已知直线y＝k(x－2)与抛物线Γ：y2＝x相交于A，B两点，M是线段AB的中点，过M作y轴的垂线交Γ于点N.‎ ‎(1)证明：抛物线Γ在点N处的切线与直线AB平行；‎ ‎(2)是否存在实数k使·＝0？若存在，求k的值；若不存在，请说明理由．‎ 解：(1)证明：由消去y并整理，‎ 得2k2x2－(8k2＋1)x＋8k2＝0.‎ 设A(x1，y1)，B(x2，y2)，则x1＋x2＝，x1x2＝4，‎ ‎∴xM＝＝，‎ yM＝k(xM－2)＝k＝.‎ 由题设条件可知，yN＝yM＝，xN＝2y＝，‎ ‎∴N.‎ 设抛物线Γ在点N处的切线l的方程为 y－＝m，‎ 将x＝2y2代入上式，得2my2－y＋－＝0.‎ ‎∵直线l与抛物线Γ相切，‎ ‎∴Δ＝1－4×‎2m×＝＝0，‎ ‎∴m＝k，即l∥AB.‎ ‎(2)假设存在实数k，使·＝0，则NA⊥NB.‎ ‎∵M是AB的中点，‎ ‎∴|MN|＝|AB|.‎ 由(1)，得|AB|＝|x1－x2|‎ ‎＝· ‎＝·＝·.‎ ‎∵MN⊥y轴，‎ ‎∴|MN|＝|xM－xN|＝－＝.‎ ‎∴＝·，解得k＝±.‎ 故存在k＝±，使·＝0.‎ ‎(二)重点高中适用作业 A级——保分题目巧做快做 ‎1．设F为抛物线C：y2＝4x的焦点，曲线y＝(k＞0)与C交于点P，PF⊥x轴，则k＝(　　)‎ A.　　　　　　　　　　 　B．1‎ C. D．2‎ 解析：选D　∵y2＝4x，∴F(1,0)．又∵曲线y＝(k＞0)与C交于点P，PF⊥x轴，∴P(1,2)．将点P(1,2)的坐标代入y＝(k＞0)，得k＝2.‎ ‎2．已知抛物线C：y2＝8x的焦点为F，准线为l，P是l上一点，Q是直线PF与C的一个交点．若＝4，则|QF|＝(　　)‎ A．3 B. C. D. 解析：选A　已知F(2,0)，设P(－2，t)，Q(x0，y0)，则＝(－4，t)，＝(x0－2，y0)．由题设可得4(x0－2)＝－4，即x0＝1，所以|QF|＝x0＋2＝3.‎ ‎3．已知抛物线x2＝4y上有一条长为6的动弦AB，则AB的中点到x轴的最短距离为(　　)‎ A. B. C．1 D．2‎ 解析：选D　设AB的中点为M，焦点为F(0,1)，过点M作准线l：y＝－1的垂线MN，垂足为N，过点A作AC⊥l于点C，过点B作BD⊥l于点D，则|MN|＝＝≥＝3，当且仅当直线AB过焦点F时等号成立，所以AB的中点到x轴的最短距离dmin＝3－1＝2.故选D.‎ ‎4．已知点A是抛物线C：x2＝2py(p＞0)上一点，O为坐标原点．若A，B是以点M(0,10)为圆心，OA的长为半径的圆与抛物线C的两个公共点，且△ABO为等边三角形，则p的值是(　　)‎ A. B. C. D. 解析：选C　如图，因为|MA|＝|OA|，所以点A在线段OM的垂直平分线上．又因为M(0,10)，所以可设A(x,5)．由tan 30°＝，得x＝.将A代入方程x2＝2py，得p＝.‎ ‎5．(2018·太原模拟)已知抛物线y2＝4x的焦点为F，过焦点F的直线交该抛物线于A，B两点，O为坐标原点，若|AB|＝6，则△AOB的面积为(　　)‎ A. B．2 C．2 D．4‎ 解析：选A　因为抛物线y2＝4x的焦点F的坐标为(1,0)，当直线AB垂直于x轴时，|AB|＝4，不满足题意，所以设直线AB的方程为y＝k(x－1)，与y2＝4x联立，消去x得ky2－4y－4k＝0.设A(x1，y1)，B(x2，y2)，则y1＋y2＝，y1y2＝－4，所以|y1－y2|＝ ，因为|‎ AB|＝|y1－y2|＝6，所以4＝6，解得k＝±，所以|y1－y2|＝＝2，所以△AOB的面积为×1×2＝，故选A.‎ ‎6．过点P(－2,0)的直线与抛物线C：y2＝4x相交于A，B两点，且|PA|＝|AB|，则点A到抛物线C的焦点的距离为________．‎ 解析：设A(x1，y1)，B(x2，y2)，分别过点A，B作直线x＝－2的垂线，垂足分别为D，E，∵|PA|＝|AB|，‎ ‎∴又得x1＝，‎ 则点A到抛物线C的焦点的距离为1＋＝.‎ 答案： ‎7．(2017·山东高考)在平面直角坐标系xOy中，双曲线－＝1(a>0，b>0)的右支与焦点为F的抛物线x2＝2py(p>0)交于A，B两点．若|AF|＋|BF|＝4|OF|，则该双曲线的渐近线方程为________．‎ 解析：设A(x1，y1)，B(x2，y2)，由抛物线的定义可知 ‎|AF|＝y1＋，|BF|＝y2＋，|OF|＝，‎ 由|AF|＋|BF|＝y1＋＋y2＋＝y1＋y2＋p＝4|OF|＝2p，得y1＋y2＝p.‎ 联立消去x，得a2y2－2pb2y＋a2b2＝0，‎ 所以y1＋y2＝，所以＝p，‎ 即＝，故＝，‎ 所以双曲线的渐近线方程为y＝±x.‎ 答案：y＝±x ‎8．已知直线y＝a交抛物线y＝x2于A，B两点．若该抛物线上存在点C，使得∠ACB为直角，则实数a的取值范围为________．‎ 解析：如图，设C(x0，x)(x≠a)，A(－，a)，B(，a)，‎ 则＝(－－x0，a－x)，＝(－x0，a－x)．‎ ‎∵CA⊥CB，∴·＝0，‎ 即－(a－x)＋(a－x)2＝0，(a－x)(－1＋a－x)＝0.‎ ‎∴x＝a－1≥0，∴a≥1.‎ 答案：[1，＋∞)‎ ‎9.如图所示，已知抛物线C：y2＝4x的焦点为F，直线l经过点F且与抛物线C相交于A，B两点．‎ ‎(1)若线段AB的中点在直线y＝2上，求直线l的方程；‎ ‎(2)若线段|AB|＝20，求直线l的方程．‎ 解：(1)由已知，得抛物线的焦点为F(1,0)．‎ 因为线段AB的中点在直线y＝2上，‎ 所以直线l的斜率存在，‎ 设直线l的斜率为k，A(x1，y1)，B(x2，y2)，‎ AB的中点M(x0，y0)，由 得(y1＋y2)(y1－y2)＝4(x1－x2)，‎ 所以2y0k＝4.‎ 又y0＝2，所以k＝1，‎ 故直线l的方程是y＝x－1.‎ ‎(2)设直线l的方程为x＝my＋1，与抛物线方程联立得 消去x，得y2－4my－4＝0，‎ 所以y1＋y2＝‎4m，y1y2＝－4，Δ＝16(m2＋1)>0.‎ ‎|AB|＝|y1－y2|‎ ‎＝· ‎＝· ‎＝4(m2＋1)．‎ 所以4(m2＋1)＝20，解得m＝±2，‎ 所以直线l的方程是x＝±2y＋1，即x±2y－1＝0.‎ ‎10.(2018·合肥模拟)如图，点O为坐标原点，直线l经过抛物线C：y2＝4x的焦点F.设点A是直线l与抛物线C在第一象限的交点．以点F为圆心，|FA|为半径的圆与x轴负半轴的交点为点B.‎ ‎(1)若点O到直线l的距离为，求直线l的方程；‎ ‎(2)试判断直线AB与抛物线C的位置关系，并给出证明．‎ 解：(1)由题易知，抛物线C的焦点为F(1,0)，‎ 当直线l的斜率不存在时，即x＝1时，不符合题意．‎ 当直线l的斜率存在时，设直线l的方程为y＝k(x－1)，‎ 即kx－y－k＝0.‎ 所以＝，解得k＝±.‎ 即直线l的方程为y＝±(x－1)．‎ ‎(2)直线AB与抛物线C相切，证明如下：‎ 设A(x0，y0)，则y＝4x0.‎ 因为|BF|＝|AF|＝x0＋1，所以B(－x0,0)．‎ 所以直线AB的方程为y＝(x＋x0)，‎ 整理得，x＝－x0，‎ 把上式代入y2＝4x得y0y2－8x0y＋4x0y0＝0，‎ Δ＝64x－16x0y＝64x－64x＝0，‎ 所以直线AB与抛物线C相切．‎ B级——拔高题目稳做准做 ‎1．(2016·全国卷Ⅰ)以抛物线C的顶点为圆心的圆交C于A，B两点，交C的准线于D，E两点．已知|AB|＝4，|DE|＝2，则C的焦点到准线的距离为(　　)‎ A．2 B．4‎ C．6 D．8‎ 解析：选B　设抛物线的方程为y2＝2px(p>0)，圆的方程为x2＋y2＝r2.∵|AB|＝4，|DE|＝2，抛物线的准线方程为x＝－，∴不妨设A，D.∵点A，D在圆x2＋y2＝r2上，∴∴＋8＝＋5，解得p＝4(负值舍去)．‎ ‎∴C的焦点到准线的距离为4.‎ ‎2．设抛物线C：y2＝2px(p>0)的焦点为F，点M在C上，|MF|＝5.若以MF为直径的圆过点(0,2)，则抛物线C的方程为(　　)‎ A．y2＝4x或y2＝8x B．y2＝2x或y2＝8x C．y2＝4x或y2＝16x D．y2＝2x或y2＝16x 解析：选C　由已知得抛物线的焦点F，设点A(0,2)，M(x0，y0)，则＝，＝.由已知得，·＝0，即y－8y0＋16＝0，因而y0＝4，M.由|MF|＝5得，‎ ＋＝5，又p＞0，解得p＝2或p＝8，所以抛物线C的方程为y2＝4x或y2＝16x.‎ ‎3．过抛物线x2＝4y的焦点F作直线AB，CD与抛物线交于A，B，C，D四点，且AB⊥CD，则·＋·的最大值为(　　)‎ A．－4 B．－16‎ C．4 D．－8‎ 解析：选B　设A(xA，yA)，B(xB，yB)，‎ 依题意可得，·＝－(||·||)．‎ 又因为||＝yA＋1，||＝yB＋1，‎ 所以·＝－(yAyB＋yA＋yB＋1)．‎ 设直线AB的方程为y＝kx＋1(k≠0)，‎ 联立x2＝4y，可得y2－(2＋4k2)y＋1＝0，‎ 所以yA＋yB＝4k2＋2，yAyB＝1，‎ 所以·＝－(4k2＋4)．‎ 同理：·＝－.‎ 所以·＋·＝－≤－16.‎ 当且仅当k＝±1时等号成立．‎ ‎4．(2018·长春模拟)过抛物线y2＝4x的焦点作倾斜角为45°的直线l交抛物线于A，B两点，O为坐标原点，则△OAB的面积为________．‎ 解析：由题意知，抛物线焦点为(1,0)，直线l的方程为y＝x－1，与抛物线方程联立，得消去x，得y2－4y－4＝0，设A，B的坐标分别为(x1，y1)，(x2，y2)，则y1＋y2＝4，y1y2＝－4，|y1－y2|＝＝4，从而△OAB的面积为××|y1－y2|＝2.‎ 答案：2 ‎5.如图，已知抛物线C：y2＝2px(p＞0)，焦点为F，过点G(p,0)作直线l交抛物线C于A，M两点，设A(x1，y1)，M(x2，y2)．‎ ‎(1)若y1y2＝－8，求抛物线C的方程；‎ ‎(2)若直线AF与x轴不垂直，直线AF交抛物线C于另一点B，直线BG交抛物线C于另一点N.求证：直线AB与直线MN斜率之比为定值．‎ 解：(1)设直线AM的方程为x＝my＋p，‎ 代入y2＝2px得y2－2mpy－2p2＝0，‎ 则y1y2＝－2p2＝－8，得p＝2.‎ ‎∴抛物线C的方程为y2＝4x.‎ ‎(2)证明：设B(x3，y3)，N(x4，y4)．‎ 由(1)可知y3y4＝－2p2，y1y3＝－p2.‎ 又直线AB的斜率kAB＝＝，‎ 直线MN的斜率kMN＝＝，‎ ‎∴＝＝＝＝2.‎ 故直线AB与直线MN斜率之比为定值．‎ ‎6．(2018·武汉调研)已知直线y＝k(x－2)与抛物线Γ：y2＝x相交于A，B两点，M是线段AB的中点，过M作y轴的垂线交Γ于点N.‎ ‎(1)证明：抛物线Γ在点N处的切线与直线AB平行；‎ ‎(2)是否存在实数k使·＝0？若存在，求k的值；若不存在，请说明理由．‎ 解：(1)证明：由消去y并整理，‎ 得2k2x2－(8k2＋1)x＋8k2＝0.‎ 设A(x1，y1)，B(x2，y2)，则x1＋x2＝，x1x2＝4，‎ ‎∴xM＝＝，‎ yM＝k(xM－2)＝k＝.‎ 由题设条件可知，yN＝yM＝，xN＝2y＝，‎ ‎∴N.‎ 设抛物线Γ在点N处的切线l的方程为 y－＝m，‎ 将x＝2y2代入上式，得2my2－y＋－＝0.‎ ‎∵直线l与抛物线Γ相切，‎ ‎∴Δ＝1－4×‎2m×＝＝0，‎ ‎∴m＝k，即l∥AB.‎ ‎(2)假设存在实数k，使·＝0，则NA⊥NB.‎ ‎∵M是AB的中点，‎ ‎∴|MN|＝|AB|.‎ 由(1)，得|AB|＝|x1－x2|‎ ‎＝· ‎＝·＝·.‎ ‎∵MN⊥y轴，‎ ‎∴|MN|＝|xM－xN|＝－＝.‎ ‎∴＝·，解得k＝±.‎ 故存在k＝±，使·＝0.‎