【数学】2019届一轮复习人教B版　数列问题新情境，理解题意最关键学案 10页

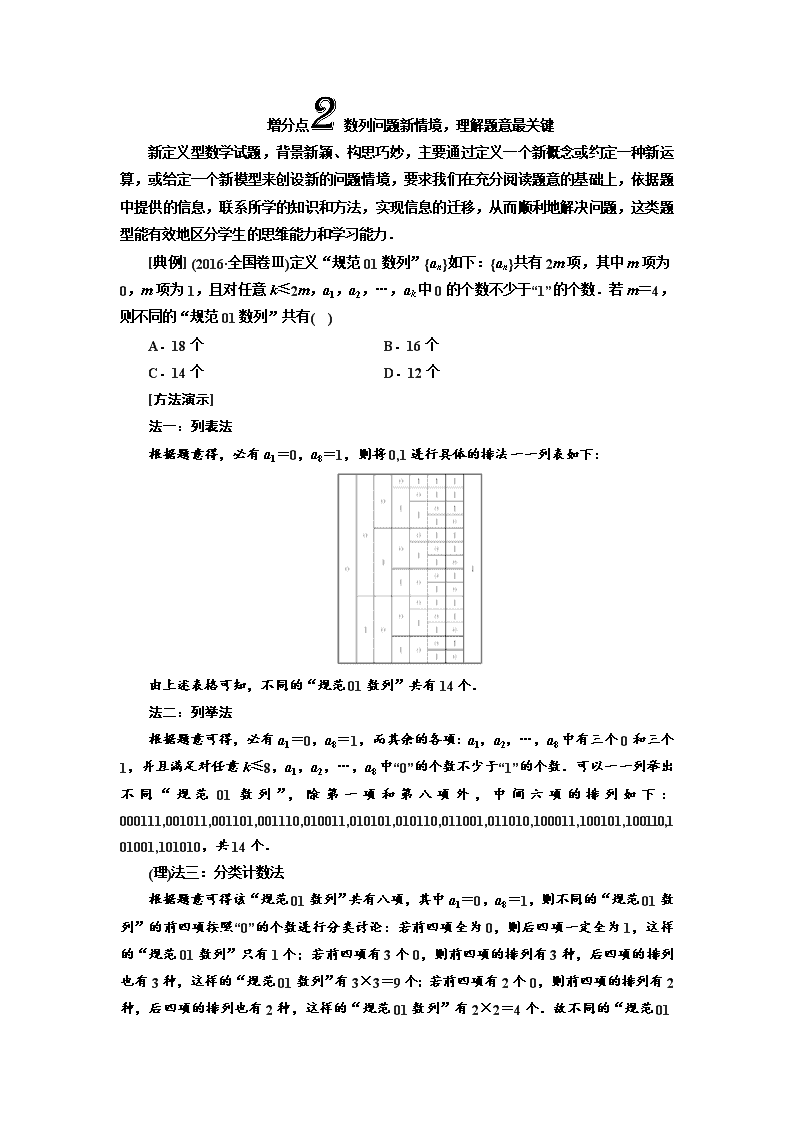
增分点 数列问题新情境，理解题意最关键 新定义型数学试题，背景新颖、构思巧妙，主要通过定义一个新概念或约定一种新运算，或给定一个新模型来创设新的问题情境，要求我们在充分阅读题意的基础上，依据题中提供的信息，联系所学的知识和方法，实现信息的迁移，从而顺利地解决问题，这类题型能有效地区分学生的思维能力和学习能力．‎ ‎[典例] (2016·全国卷Ⅲ)定义“规范01数列”{an}如下：{an}共有‎2m项，其中m项为0，m项为1，且对任意k≤‎2m，a1，a2，…，ak中0的个数不少于“‎1”‎的个数．若m＝4，则不同的“规范01数列”共有( )‎ A．18个 B．16个 C．14个 D．12个 ‎[方法演示] ‎ 法一：列表法 根据题意得，必有a1＝0，a8＝1，则将0,1进行具体的排法一一列表如下：‎ 由上述表格可知，不同的“规范01数列”共有14个．‎ 法二：列举法 根据题意可得，必有a1＝0，a8＝1，而其余的各项：a1，a2，…，a8中有三个0和三个1，并且满足对任意k≤8，a1，a2，…，a8中“0”的个数不少于“1”的个数．可以一一列举出不同“规范01数列”，除第一项和第八项外，中间六项的排列如下：000111,001011,001101,001110,010011,010101,010110,011001,011010,100011,100101,100110,101001,101010，共14个．‎ ‎(理)法三：分类计数法 根据题意可得该“规范01数列”共有八项，其中a1＝0，a8＝1，则不同的“规范01数列”的前四项按照“0”的个数进行分类讨论：若前四项全为0，则后四项一定全为1，这样的“规范01数列”只有1个；若前四项有3个0，则前四项的排列有3种，后四项的排列也有3种，这样的“规范01数列”有3×3＝9个；若前四项有2个0，则前四项的排列有2种，后四项的排列也有2种，这样的“规范01数列”有2×2＝4个．故不同的“‎ 规范01数列”的总数为14种．‎ ‎(理)法四：填“空”格法 根据题意可得该“规范01数列”共有八项，其中，a1＝0，a8＝1，则不同的“规范01数列”采用“0,1”填“空”的方式计数．具体如下：‎ 将“规范01数列”的八个项按照序号从小到大的方式以“空”格形式表示，再用“0,1”去填“空”格．可以得到一些不同的“规范01数列”．‎ 第7个“空”格填“1”，则其余5个“空”格只需选2个“空”格填“1”，然后再排除第2个和第3个“空”格连排“1”的情况，有C－1＝9(种)；‎ 第7个“空”格填“0”，显然第6个“空”格只能填“1”，再对第5个“空”格分类讨论：若第5个“空”格填“0”，第4个“空”格只能填“1”的方法只有2种；若第5个“空”格填“1”，那么最后一个“1”可以任意排的方法只有3种．故不同的“规范01数列”共有9＋2＋3＝14种．‎ 答案：C ‎[解题师说]‎ 可以从以下三个方面解决此类问题．‎ ‎(1)提取新定义的信息，明确新定义的名称和符号；‎ ‎(2)深刻理解新定义的概念、法则、性质，纵横联系探求解题方法，比较相近知识点，明确不同点；‎ ‎(3)对新定义中提取的知识进行等价转换，其中提取、化归与转化是解题的关键，也是解题的难点．‎ 新定义问题的解题思路为：‎ ‎①若新定义是运算法则，直接按照运算法则计算即可；‎ ‎②若新定义是性质，要判断性质的适用性，能否利用定义外延；也可用特殊值排除等方法．‎ ‎[应用体验]‎ ‎1．(2018·茂名一模)我国古代数学著作《九章算术》有如下问题：“今有金箠，长五尺，斩本一尺，重四斤，斩末一尺，重二斤，问次一尺各重几何？”意思是：“现有一根金箠，长五尺，一头粗，一头细，在粗的一端截下1尺，重4斤，在细的一端截下1尺，重2斤，问依次每一尺各重多少斤？”根据上题的已知条件，若金箠由粗到细是均匀变化的，问第二尺与第四尺的重量之和为( )‎ A．6斤 B．9斤 C．9.5斤 D．12斤 解析：选A 依题意， 金箠由粗到细各尺的重量构成一个等差数列，设首项a1＝4，则a5＝2，由等差数列的性质得a2＋a4＝a1＋a5＝6，所以第二尺与第四尺的重量之和为6斤．‎ ‎2．已知数列{an}中，a1＝，an＋1＝[an]＋([an]与〈an〉分别表示an的整数部分与小数部分)，则〈a2 018〉＝( )‎ A.－1 B. C.－1 D. 解析：选B 因为a1＝，an＋1＝[an]＋，所以[a1]＝1，〈a1〉＝－1，所以a2＝1＋＝2＋，a3＝2＋＝4＋(－1)，a4＝4＋＝5＋，a5＝5＋＝7＋(－1)，a6＝7＋＝8＋，…，〈a2n－1〉＝－1，〈a2n〉＝，所以〈a2 018〉＝.‎ 一、选择题 ‎1．在数列{an}中，若存在非零整数T，使得am＋T＝am对于任意的正整数n均成立，那么称数列{an}为周期数列，其中T叫做数列{an}的周期．若数列{xn}满足xn＋1＝|xn－xn－1|(n≥2，n∈N)，如x1＝1，x2＝a(a∈R，a≠0)，当数列{xn}的周期最小时，该数列的前2 018项的和是( )‎ A．672 B．673‎ C．1 344 D．1 346‎ 解析：选D 要使周期最小，即使得第一项之后的各项中尽早出现1，又已知第二项不应是0，所以1,0,1,0不符合．所以1,1,0,1,1,0，…，周期为3.又2 018＝3×672＋2，所以S2 018＝1＋1＋2×672＝1 346.‎ ‎2．我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯( )‎ A．1盏 B．3盏 C．5盏 D．9盏 解析：选B 每层塔所挂的灯数从上到下构成等比数列，记为{an}，则前7项的和S7＝381，公比q＝2，依题意，得＝381，解得a1＝3.‎ ‎3．《九章算术》是我国古代数学名著，在其中有道“竹九节问题”：“今有竹九节，下三节容量四升，上四节容量三升．问中间二节欲均容各多少？”意思为：今有竹九节，下三节容量和为‎4升，上四节容量之和为‎3升，且每一节容量变化均匀(即每节容量成等差数列)．问每节容量各为多少？在这个问题中，中间一节的容量为( )‎ A. B. C. D. 解析：选C 设从最下节往上的容量构成等差数列{an}，公差为d.则即 解得a1＝，d＝－.‎ 中间为第五节，即a5＝a1＋4d＝＋4×＝.‎ ‎4．对于一切实数x，令[x]为不大于x的最大整数，则函数f(x)＝[x]称为高斯函数或取整函数．若an＝f，n∈N*，Sn为数列{an}的前n项和，则S3n＝( )‎ A.n2－n B.n2＋n C．3n2－2n D.n2－n 解析：选A 由题意，当n＝3k，n＝3k＋1，n＝3k＋2时均有an＝f＝＝k，所以S3n＝0＋0＋1＋1＋＋2＋2＋＋…＋(n－1)＋(n－1)＋(n－1＋n＝3××(n－1)＋n＝n2－n.‎ ‎5．(2018·泉州模拟)若存在常数k(k∈N*，k≥2)，q，d，使得无穷数列{an}满足an＋1＝则称数列{an}为“段比差数列”，其中常数k，q，d分别叫做段长、段比、段差．设数列{bn}为“段比差数列”．若{bn}的首项、段长、段比、段差分别为1,3,0,3，则b2 019＝( )‎ A．3 B．4‎ C．5 D．6‎ 解析：选D 法一：∵{bn}的首项、段长、段比、段差分别为1,3,0,3，∴b2 017＝0×b2 016＝0，∴b2 018＝b2 017＋3＝3，∴b2 019＝b2 018＋3＝6.‎ 法二：∵{bn}的首项、段长、段比、段差分别为1,3,0,3，∴b1＝1，b2＝4，b3＝7，b4＝0×b3＝0，b5＝b4＋3＝3，b6＝b5＋3＝6，b7＝0×b6＝0，……，∴当n≥4时，{bn}是周期为3的周期数列．∴b2 019＝b6＝6.‎ ‎6．由n(n≥2)个不同的数构成的数列a1，a2，…，an中，若1≤i1)的中点，设数列{an}，{bn}满足：＝＋ (n∈N*)，给出下列四个命题，其中假命题是( )‎ A．数列{an}是单调递增数列，数列{bn}是单调递减数列 B．数列{an＋bn}是等比数列 C．数列(n>1，n∈N*)既有最小值，又有最大值 D．在△ABC中，若C＝90°，CA＝CB，则||最小时，an＋bn＝ 解析：选C 由B＝＝(－)，＝，＝＋B＝＋(－)＝＋，所以an＝1－，bn＝－1，则数列{an}是单调递增数列，数列{bn}是单调递减数列，故A正确；数列{an＋bn}中， an＋bn＝，a1＋b1＝，即数列{an＋bn}是首项为，公比为的等比数列，故B正确；当n>1时，＝＝－1＋单调递增，有最小值，无最大值，故C错误；在△ABC中， 若C＝90°，CA＝CB，则||2＝(a＋b)2＋2an·＝(a＋b)2，a＋b＝2＋2＝5×2－6×n＋2＝52＋，当n＝1时，a＋b取得最小值，即当||最小时，an＋bn＝，故D正确．‎ ‎9．(2017·全国卷Ⅰ)几位大学生响应国家的创业号召，开发了一款应用软件．为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动．这款软件的激活码为下面数学问题的答案：已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16，…，其中第一项是20，接下来的两项是20,21，再接下来的三项是20,21,22，依此类推．求满足如下条件的最小整数N：N>100且该数列的前N项和为2的整数幂．那么该款软件的激活码是( )‎ A．440 B．330‎ C．220 D．110‎ 解析：选A 设第一项为第1组，接下来的两项为第2组，再接下来的三项为第3组，依此类推，则第n组的项数为n，前n组的项数和为.‎ 由题意可知，N>100，令>100，‎ 得n≥14，n∈N*，即N出现在第13组之后．‎ 易得第n组的所有项的和为＝2n－1，前n组的所有项的和为－n＝2n＋1－n－2.‎ 设满足条件的N在第k＋1(k∈N*，k≥13)组，且第N项为第k＋1组的第t(t∈N*)个数，‎ 若要使前N项和为2的整数幂，则第k＋1组的前t项的和2t－1应与－2－k互为相反数，‎ 即2t－1＝k＋2，∴2t＝k＋3，∴t＝log2(k＋3)，‎ ‎∴当t＝4，k＝13时，N＝＋4＝95<100，不满足题意；‎ 当t＝5，k＝29时，N＝＋5＝440；‎ 当t>5时，N>440，故选A.‎ ‎10.如图，点列{An}，{Bn}分别在某锐角的两边上，且|AnAn＋1|＝|An＋1An＋2|，An≠An＋2，n∈N*，|BnBn＋1|＝|Bn＋1Bn＋2|，Bn≠Bn＋2，n∈N*(P≠Q表示点P与Q不重合)．若dn＝|AnBn|，Sn为△AnBnBn＋1的面积，则( )‎ A．{Sn}是等差数列 B．{S}是等差数列 C．{dn}是等差数列 D．{d}是等差数列 解析：选A 由题意，过点A1，A2，A3，…，An，An＋1，…分别作直线B1Bn＋1的垂线，高分别记为h1，h2，h3，…，hn，hn＋1，…，根据平行线的性质，得h1，h2，h3，…，hn，hn＋1，…成等差数列，又Sn＝×|BnBn＋1|×hn，|BnBn＋1|为定值，所以{Sn}是等差数列．‎ ‎11．设无穷数列{an}，如果存在常数A，对于任意给定的正数ε(无论多小)，总存在正整数N，使得n>N时，恒有|an－A|<ε成立，则称数列{an}的极限为A.给出下列四个无穷数列：‎ ‎①{(－1)n×2}；‎ ‎②；‎ ‎③；‎ ‎④{1×2＋2×22＋3×23＋…＋n×2n}，‎ 其极限为2的共有( )‎ A．4个 B．3个 C．2个 D．1个 解析：选D 对于①，|an－2|＝|(－1)n×2－2|＝2×|(－1)n－1|，当n是偶数时，|an－2|＝0；当n是奇数时，|an－2|＝4，所以不符合数列{an}的极限定义，即2不是数列{(－1)n×2}的极限．‎ 对于②，|an－2|＝ ＝ ＝1＋>1，所以对于任意给定的正数ε(无论多小)，不存在正整数N，使得n>N时，恒有|an－2|<ε，即2不是数列 的极限．‎ 对于③，由|an－2|＝＝‎ ＝<ε，得n>1－log2ε，即对于任意给定的正数ε(无论多小)，总存在正整数N，使得n>N时，恒有|an－2|<ε成立，所以2是数列 的极限．‎ 对于④，|an－2|＝|1×2＋2×22＋3×23＋…＋n×2n－2|＝2×22＋3×23＋…＋n×2n>1，所以对于任意给定的正数ε(无论多小)，不存在正整数N，使得n>N时，恒有|an－2|<ε，即2不是数列{1×2＋2×22＋3×23＋…＋n×2n}的极限．‎ 综上所述，极限为2的数列共有1个．‎ ‎12．对于数列{xn}，若对任意n∈N*，都有xn＋2－xn＋1，‎ 化简得t(n2－4n)>n－2，‎ 由题知，当n≥5时，t(n2－4n)>n－2恒成立，‎ 所以t>＝恒成立．‎ 令n－2＝x(x≥3，x∈N*)，设y＝x－(x≥3，x∈N*)．‎ 易知函数y＝x－在[3，＋∞)上是增函数，‎ 所以当x＝3时，y取得最小值，‎ 所以当x＝3时，＝取得最大值，‎ 即当n≥5时，的最大值为，‎ 则t的取值范围是.‎ 二、填空题 ‎13．在数列中，n∈N*，若＝k(k为常数)，则称为“等差比数列”，下列是对“等差比数列”的判断：‎ ‎①k不可能为0；‎ ‎②等差数列一定是“等差比数列”；‎ ‎③等比数列一定是“等差比数列”；‎ ‎④“等差比数列”中可以有无数项为0.‎ 其中判断正确的序号是________．‎ 解析：由等差比数列的定义可知，k不为0，所以①正确；‎ 当等差数列的公差为0，即等差数列为常数列时，等差数列不是等差比数列，所以②错误；‎ 当是等比数列，且公比q＝1时，不是等差比数列，所以③错误；‎ 数列0,1,0,1，…是等差比数列，该数列中有无数多个0，所以④正确．‎ 答案：①④‎ ‎14．(2018·兰州模拟)对于正整数n，设曲线y＝xn(1－x)在x＝2处的切线与平面直角坐标系的y轴交点的纵坐标为an，则数列的前10项和等于__________．‎ 解析：y′＝nxn－1－(n＋1)xn＝[n－(n＋1)x]xn－1，当x＝2时，y＝2n(1－2)＝－2n，所以曲线在点(2，－2n)处的切线的斜率k＝(－n－2)×2n－1，切线方程为y－(－2n)＝(－n－2)×2n－1×(x－2)，当x＝0时，y＝(n＋1)×2n，所以an＝(n＋1)×2n，‎ 所以log2＝log22n＝n，即数列是首项为1，公差为1的等差数列，其前10项的和为×10＝55.‎ 答案：55‎ ‎15．(2018·昆明质检)在平面直角坐标系上，有一点列P1，P2，…，Pn，…(n∈N*)，设点Pn的坐标为(n，an)，其中an＝(n∈N*)，过点Pn，Pn＋1的直线与两坐标轴所围成的三角形的面积为bn，设Sn表示数列{bn}的前n项和，则S5＝__________.‎ 解析：由题意得，过点Pn，Pn＋1的直线为＝，即2x＋n(n＋1)y－2(2n＋1)＝0.‎ 令y＝0，得x＝2n＋1，令x＝0，得y＝，‎ 所以bn＝×(2n＋1)×＝4＋＝4＋－，‎ 所以S5＝4×5＋1－＋－＋…＋－＝.‎ 答案： ‎16．定义：max{a，b}表示实数a，b中的较大者．已知数列{an}满足a1＝a(a>0)，a2＝1，an＋2＝(n∈N*)，若a2 019＝‎2a，记数列{an}的前n项和为Sn，则S2 019的值为________．‎ 解析：由题意知，a3＝＝，a4＝，若≥2，即a≤2，则a4＝，a5＝＝4，a6＝＝a，a7＝1，……，故数列{an}是周期为5的数列，故a2 019＝a403×5＋4＝a4＝＝‎2a(a>0)，所以a＝2，S2 019＝403×(a1＋a2＋a3＋a4＋a5)＋a1＋a2＋a3＋a4＝403×(2＋1＋2＋4＋4)＋2＋1＋2＋4＝5 248.若<2，即a>2，则a4＝4，a5＝＝‎2a，a6＝＝a，a7＝1，……，故数列{an}是周期为5的数列，故a2 019＝a403×5＋4＝a4＝4＝‎2a(a>0)，因为a>2，所以a＝2不合题意．综上，S2 019＝5 248.‎ 答案：5 248‎