【数学】2020届一轮复习人教A版解不等式的方法（文）学案 5页

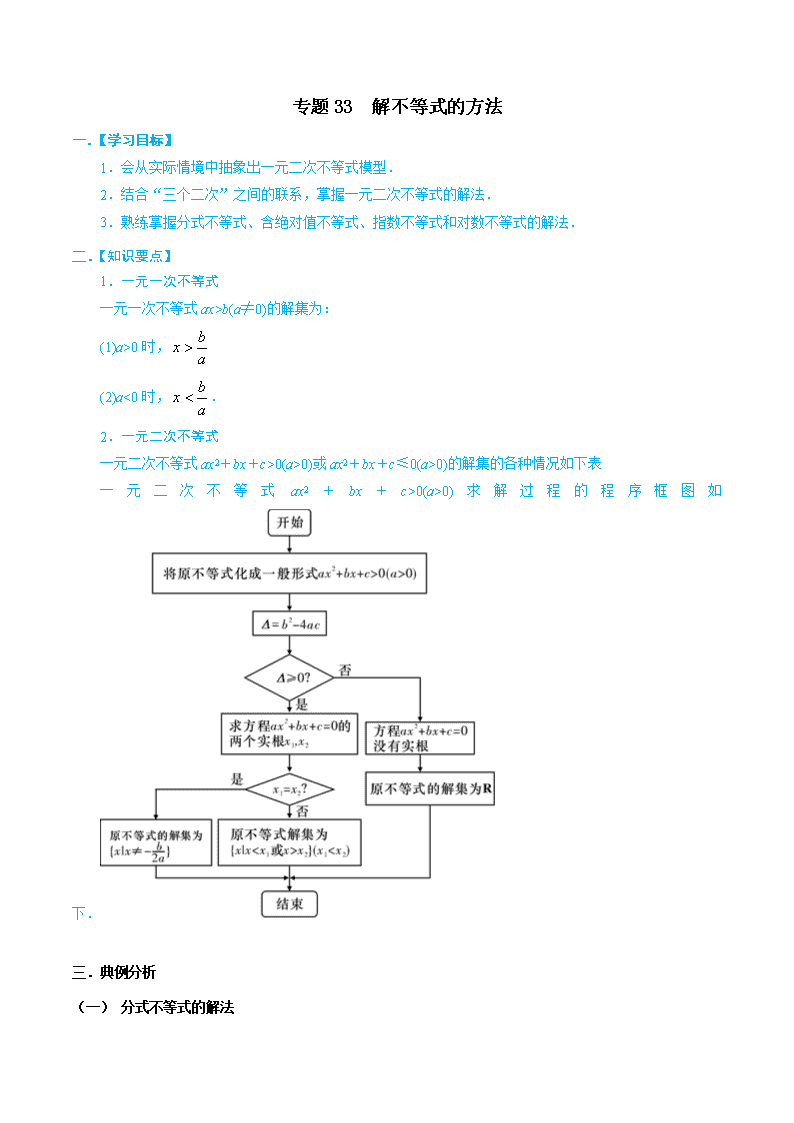
专题33 解不等式的方法 一．【学习目标】‎ ‎1．会从实际情境中抽象出一元二次不等式模型．‎ ‎2．结合“三个二次”之间的联系，掌握一元二次不等式的解法．‎ ‎3．熟练掌握分式不等式、含绝对值不等式、指数不等式和对数不等式的解法．‎ 二．【知识要点】‎ ‎1．一元一次不等式 一元一次不等式ax>b(a≠0)的解集为：‎ ‎(1)a>0时，‎ ‎(2)a<0时，．‎ ‎2．一元二次不等式 一元二次不等式ax2＋bx＋c>0(a>0)或ax2＋bx＋c≤0(a>0)的解集的各种情况如下表 一元二次不等式ax2＋bx＋c>0(a>0)求解过程的程序框图如下． ‎ 三．典例分析 ‎（一） 分式不等式的解法 ‎1．设集合，集合，则（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】A＝{x|﹣2＜x＜4}，B＝{x|x＞﹣1}；‎ ‎∴A∩B＝{x|﹣1＜x＜4}．‎ 故选：D．‎ 练习1．若函数是奇函数，则使成立的的取值范围是( )‎ A． B． C． D．‎ ‎【答案】D 练习2．已知a∈R，不等式的解集为p，且－2∉p，则a的取值范围为(　　)‎ A．(－3，＋∞) B．(－3,2)‎ C．(－∞，2)∪(3，＋∞) D．(－∞，－3)∪[2，＋∞)‎ ‎【答案】D ‎【解析】‎ ‎∵－2∉p，∴<1或－2＋a＝0，解得a≥2或a<－3.‎ 点睛：解分式不等式时，一般是把分式不等式转化为整式不等式求解，如果不等号中含有“等号”，但在转化时特别要注意分母不为零，否则就是错误的结论．本题中－2不是题中不等式的解，则就有使分母为零的一种情形，不能遗漏．‎ 练习3．已知函数f(x)(x∈R)的图象如图所示，f′(x)是f(x)的导函数，则不等式(x2－2x－3)f′(x ‎)>0的解集为(　　)‎ A．(－∞，－2)∪(1，＋∞)‎ B．(－∞，－2)∪(1,2)‎ C．(－∞，－1)∪(－1,0)∪(2，＋∞)‎ D．(－∞，－1)∪(－1,1)∪(3，＋∞)‎ ‎【答案】D ‎【解析】由f(x)的图象可知，在(－∞，－1)，(1，＋∞)上，f′(x)>0，在(－1,1)上，f′(x)<0.由(x2－2x－3)·f′(x)>0，得或即或，所以不等式的解集为(－∞，－1)∪(－1,1)∪(3，＋∞)． ‎ 故实数m的取值范围为 ‎ ‎(3)∵f(x)≤n2-2bn+1对所有x∈[-1,1]恒成立,‎ ‎∴[f(x)]max≤n2-2bn+1,‎ 又[f(x)]max=f(0)=1,‎ ‎∴n2-2bn+1≥1,即n2-2bn≥0在b∈[-1,1]上恒成立.令h(b)=-2nb+n2,‎ ‎∴h(b)=-2nb+n2在b∈[-1,1]上恒大于等于0.‎ ‎∴‎ 即 由①得 解得n≥0或n≤-2.‎ 同理由②得n≤0或n≥2.‎ ‎∴n∈(-∞,-2]∪{0}∪[2,+∞).‎ 故n的取值范围是(-∞,-2]∪{0}∪[2,+∞)‎ 练习3．已知二次函数满足，且.‎ ‎（1）求的解析式；‎ ‎（2）若函数的最小值为，且，求实数的值；‎ ‎（3）若对任意互不相同的，都有成立，‎ 求实数的取值范围.‎ ‎【答案】（1）f（x）=x2-2x+3；（2）m的值为-1；（3）[6，+∞）．‎ ‎【解析】（1）设二次函数的解析式为f（x）=ax2+bx+c （a≠0） 由f（0）=3得c=3， 故f（x）=ax2+bx+3． 因为f（x+1）-f（x）=2x-1， 所以a（x+1）2+b（x+1）+3-（ax2+bx+3）=2x-1． 即2ax+a+b=2x-1， 根据系数对应相等 ，解得， ， 所以f（x）=x2-2x+3；学-科网 （2）由于f（x）=x2-2x+3=（x-1）2+2， 函数y=f（log3x+m）=（log3x+m-1）2+2， 令t=log3x，（-1≤t≤1），则y=（t+m-1）2+2， 由题意可知最小值只能在端点处取得， 若t=1时，取得最小值3，即有m2+2=3，解得m=±1， 当m=1时，函数y=t2+2在区间[-1，1]的最小值为2， 则m=1舍去； 当m=-1时，函数y=（t-2）2+2在区间[-1，1]递减， 可得t=1时取得最小值且为3； 若t=-1时，取得最小值3，即有（m-2）2+2=3，解得m=3或1， 当m=1时，函数y=t2+2在区间[-1，1]的最小值为2， 则m=1舍去； 当m=3时，函数y=（t+2）2+2在区间[-1，1]递增， 可得t=-1时取得最小值且为3．‎ 结合可知.‎