【数学】2020届北京一轮复习通用版6-1数列的概念及其表示 5页

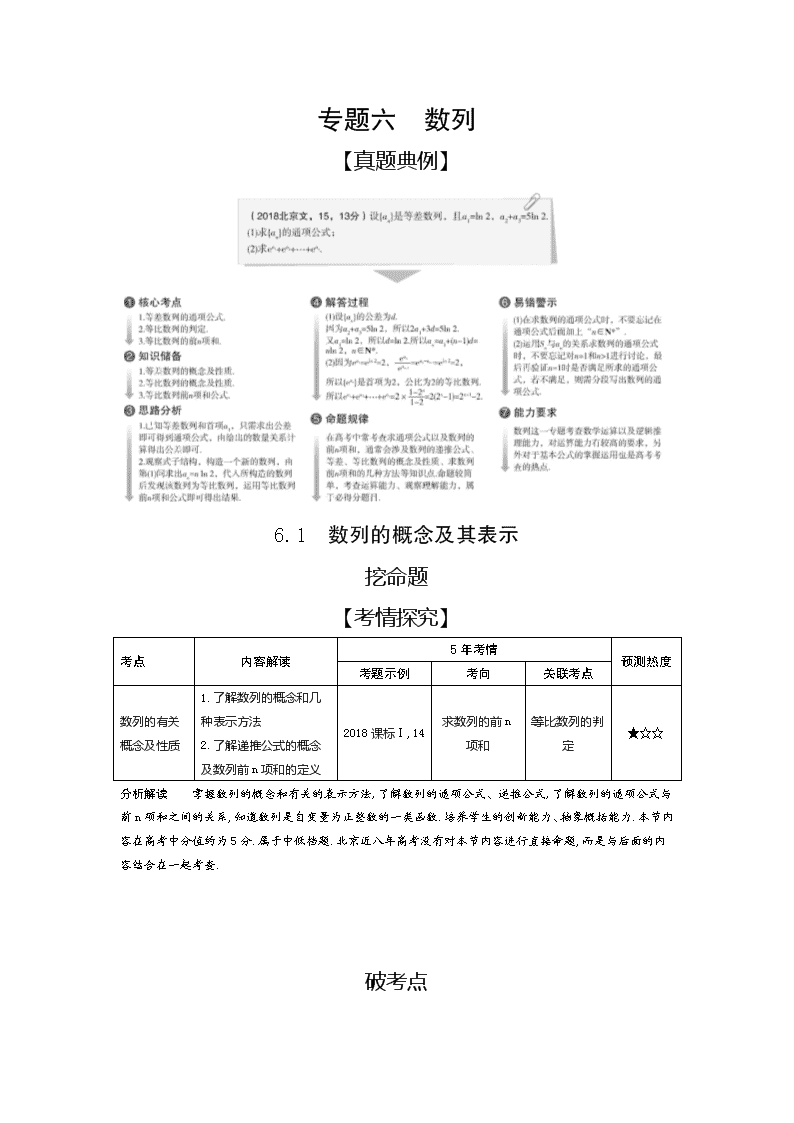
专题六　数列 ‎【真题典例】‎ ‎6.1　数列的概念及其表示 挖命题 ‎【考情探究】‎ 考点 内容解读 ‎5年考情 预测热度 考题示例 考向 关联考点 数列的有关概念及性质 ‎1.了解数列的概念和几种表示方法 ‎2.了解递推公式的概念及数列前n项和的定义 ‎2018课标Ⅰ,14‎ 求数列的前n项和 等比数列的判定 ‎★☆☆‎ 分析解读　　掌握数列的概念和有关的表示方法,了解数列的通项公式、递推公式,了解数列的通项公式与前n项和之间的关系,知道数列是自变量为正整数的一类函数.培养学生的创新能力、抽象概括能力.本节内容在高考中分值约为5分.属于中低档题.北京近八年高考没有对本节内容进行直接命题,而是与后面的内容结合在一起考查.‎ 破考点 ‎【考点集训】‎ 考点　数列的有关概念及性质 ‎1.在数列{an}中,a1=0,an+1=‎3‎‎+‎an‎1-‎‎3‎an,则a2 016=(　　)‎ A.2‎3‎　　　　B.‎3‎　　　　C.0　　　　D.-‎‎3‎ 答案　D　‎ ‎2.已知数列{an}满足a1=1,且an=n(an+1-an)(n∈N*),则a2=　　　;an=　　　. ‎ 答案　2;n ‎3.已知数列{an}满足an=3an-1+3n-1(n∈N*,n≥2),且a1=5,则an=　　　　. ‎ 答案　(n+4)·3n-1‎ ‎4.已知数列{an}的前n项和为Sn,且Sn=an+1-2n+2,a2=2,则an=　　　　. ‎ 答案　‎‎2,n=1‎‎2‎n‎-2,n>1‎ 炼技法 ‎【方法集训】‎ 方法1　利用an与Sn的关系求通项 ‎1.已知数列{an}的前n项和为Sn,若3Sn=2an-3n,则a2 018=(　　)‎ A.22 018-1　　　　B.32 018-6　　　　C.‎1‎‎2‎‎2 018‎-‎7‎‎2‎　　　　D.‎1‎‎3‎‎2 018‎-‎‎10‎‎3‎ 答案　A　‎ ‎2.已知数列{an}的前n项和为Sn,且Sn=2an-1,则S‎6‎a‎6‎=(　　)‎ A.‎63‎‎32‎　　　　B.‎31‎‎16‎　　　　C.‎123‎‎64‎　　　　D.‎‎127‎‎128‎ 答案　A　‎ ‎3.已知数列{an}的前n项和为Sn,且a1=1,Sn=‎(n+1)‎an‎2‎,则a2 017=(　　)‎ A.2 016　　　　B.2 017　　　　C.4 032　　　　D.4 034‎ 答案　B　‎ ‎4.已知Sn为数列{an}的前n项和,且log2(Sn+1)=n+1,则数列{an}的通项公式为　　　　. ‎ 答案　an=‎‎3,n=1‎‎2‎n‎,n≥2‎ 方法2　利用递推关系求数列的通项 ‎5.已知数列{an}中,a1=1,an+1=2an+1(n∈N*),Sn为其前n项和,则S5的值为(　　)‎ A.57　　　　B.61　　　　C.62　　　　D.63‎ 答案　A　‎ ‎6.在数列{an}中,a1=1,an+1=‎2‎anan‎+2‎,则数列{an}的通项an=　　　　. ‎ 答案　‎‎2‎n+1‎ ‎7.已知数列{an}的前n项之和为Sn,若a1=2,an+1=an+2n-1+1,则S10=　　　　. ‎ 答案　1 078‎ 过专题 ‎【五年高考】‎ 统一命题、省(区、市)卷题组 ‎1.(2018课标Ⅰ,14,5分)记Sn为数列{an}的前n项和.若Sn=2an+1,则S6=　　　　. ‎ 答案　-63‎ ‎2.(2016浙江,13,6分)设数列{an}的前n项和为Sn.若S2=4,an+1=2Sn+1,n∈N*,则a1=　　　　,S5=　　　　. ‎ 答案　1;121‎ ‎3.(2015课标Ⅱ,16,5分)设Sn是数列{an}的前n项和,且a1=-1,an+1=SnSn+1,则Sn=　　　　. ‎ 答案　-‎‎1‎n ‎4.(2016课标Ⅲ,17,12分)已知各项都为正数的数列{an}满足a1=1,an‎2‎-(2an+1-1)an-2an+1=0.‎ ‎(1)求a2,a3;‎ ‎(2)求{an}的通项公式.‎ 解析　(1)由题意得a2=‎1‎‎2‎,a3=‎1‎‎4‎.‎ ‎(2)由an‎2‎-(2an+1-1)an-2an+1=0得2an+1(an+1)=an(an+1).‎ 因为{an}的各项都为正数,所以an+1‎an=‎1‎‎2‎.‎ 故{an}是首项为1,公比为‎1‎‎2‎的等比数列,因此an=‎1‎‎2‎n-1‎.‎ 评析本题主要考查了数列的递推公式及等比数列的定义,属基础题.‎ C组　教师专用题组 ‎1.(2013课标Ⅰ,14,5分)若数列{an}的前n项和Sn=‎2‎‎3‎an+‎1‎‎3‎,则{an}的通项公式是an=　　　　. ‎ 答案　(-2)n-1‎ ‎2.(2013安徽,14,5分)如图,互不相同的点A1,A2,…,An,…和B1,B2,…,Bn,…分别在角O的两条边上,所有AnBn相互平行,且所有梯形AnBnBn+1An+1的面积均相等.设OAn=an.若a1=1,a2=2,则数列{an}的通项公式是　　　　　　. ‎ 答案　an=‎‎3n-2‎ ‎3.(2014大纲全国,17,10分)数列{an}满足a1=1,a2=2,an+2=2an+1-an+2.‎ ‎(1)设bn=an+1-an,证明{bn}是等差数列;‎ ‎(2)求{an}的通项公式.‎ 解析　(1)证明:由an+2=2an+1-an+2得,‎ an+2-an+1=an+1-an+2,即bn+1=bn+2.‎ 又b1=a2-a1=1.‎ 所以{bn}是首项为1,公差为2的等差数列.‎ ‎(2)由(1)得bn=1+2(n-1),即an+1-an=2n-1.‎ 于是‎∑‎k=1‎n‎(ak+1‎-ak)=‎∑‎k=1‎n(2k-1),‎ 所以an+1-a1=n2,即an+1=n2+a1.‎ 又a1=1,所以{an}的通项公式为an=n2-2n+2.‎ ‎【三年模拟】‎ 一、选择题(每小题5分,共15分)‎ ‎1.(2017北京西城一模,7)若数列{an}的通项公式为an=|n-c|(n∈N*),则“c≤1”是“{an}为递增数列”的(　　)‎ A.充分而不必要条件　　　　B.必要而不充分条件　　　　C.充要条件　　　　D.既不充分也不必要条件 答案　A　‎ ‎2.(2019届北京海淀期中文,7)数列{an}的通项公式为an=n+an,若数列{an}单调递增,则实数a的取值范围是(　　)‎ A.(-∞,0]　　　　B.[0,+∞)　　　　C.(-∞,2)　　　　D.[1,+∞)‎ 答案　C　‎ ‎3.(2019届北京朝阳期中,8)将正奇数数列1,3,5,7,9,…依次按两项、三项分组,得到分组序列如下:(1,3),(5,7,9),(11,13),(15,17,19),…,称(1,3)为第1组,(5,7,9)为第2组,依此类推,则原数列中的2 019位于分组序列中的(　　)‎ A.第404组　　　　B.第405组　　　　C.第808组　　　　D.第809组 答案　A　‎ 二、填空题(每小题5分,共35分)‎ ‎4.(2017北京海淀期末,10)已知数列{an}满足an+1-an=2,n∈N*,且a3=3,则a1=　　　　,其前n项和Sn=　　　　. ‎ 答案　-1;n2-2n ‎5.(2017北京石景山一模,10)在数列{an}中,a1=1,an·an+1=-2(n=1,2,3,…),那么a8等于　　　　. ‎ 答案　-2‎ ‎6.(2019届北京杨镇一中10月月考文,12)已知数列{an}的通项公式为an=n2-an(n∈N*),若{an}是递增数列,则实数a的取值范围是　　　　. ‎ 答案　a<3‎ ‎7.(2019届北京人大附中期中,13)无穷数列{an}由k个不同的数组成,Sn为{an}的前n项和.若对任意n∈N*,Sn∈{2,3},则k的最大值为　　　　. ‎ 答案　4‎ ‎8.(2019届北京潞河中学10月月考文,12)数列{an}中,如果an+1=an-‎3‎‎2‎(n∈N*),且a1=‎1‎‎2‎,那么数列{an}的前5项的和S5的值为　　　　. ‎ 答案　-‎‎25‎‎2‎ ‎9.(2018北京朝阳期末,12)已知数列{an}满足an+1=an-an-1(n≥2),a1=p,a2=q(p,q∈R).设Sn=‎∑‎i=1‎nai,则a10=　　　　;S2 018=　　　　.(用含p,q的式子表示) ‎ 答案　-p;p+q ‎10.(2018北京朝阳一模,13)等比数列{an}满足如下条件:‎ ‎①a1>0;②数列{an}的前n项和Sn<1.‎ 试写出满足上述所有条件的一个数列的通项公式:　　　. ‎ 答案　an=‎1‎‎2‎n(答案不唯一)‎