新教材数学北师大版（2019）必修第二册课件：2-6-2-一 向量在几何证明中的应用 课件（67张） 67页

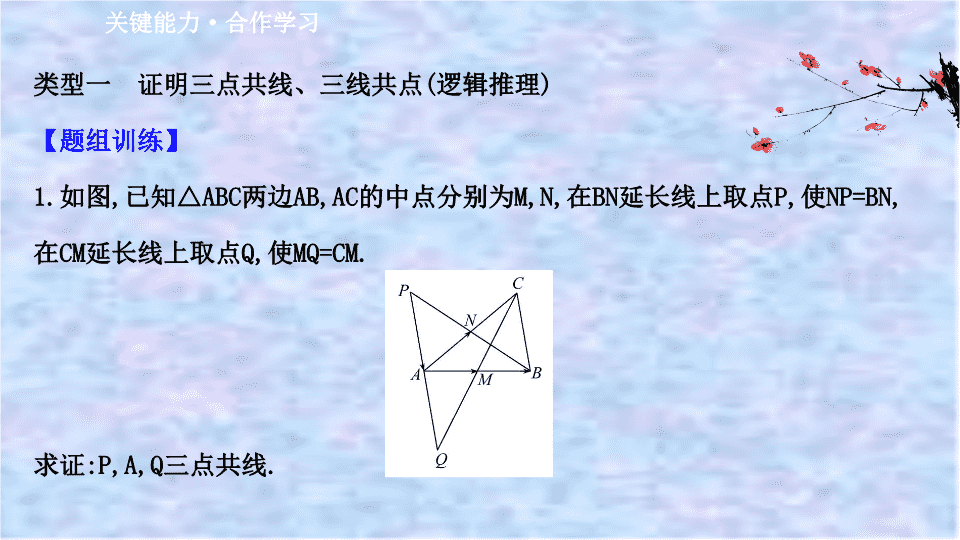
6.2　平面向量在几何、物理中的应 用举例　　　 一、向量在几何证明中的应用 关键能力·合作学习 类型一　证明三点共线、三线共点(逻辑推理) 【题组训练】 1.如图,已知△ABC两边AB,AC的中点分别为M,N,在BN延长线上取点P,使NP=BN, 在CM延长线上取点Q,使MQ=CM. 求证:P,A,Q三点共线. 2.如图,点O是平行四边形ABCD的中心,E,F分别在边CD,AB上,且 = = . 求证:点E,O,F在同一直线上. CE ED AF FB 1 2 3.已知D,E,F分别为△ABC三边BC,AC,AB的中点. 求证:AD,CF,BE相交于一点. 【证明】1.设 则 由此可得 所以 故 故 且它们有公共点A,所 以P,A,Q三点共线. AB AC   ， ，a b 1 1AN AM2 2    ， ，b a 1 1BN NP CM MQ2 2        － ， － ，b a a b PA AN NP PA ( )       － ， － － － ，b a a b QA AM MQ AQ ( )       － ， － － － ，b a a b PA AQ  ， PA AQ   ， 2.设 由 知E,F分别是CD,AB的三等分点,所以 又O为 和 的公共点,所以点E,O,F在同一条直线上. AB AD   ， ，m n CE AF 1 ED FB 2   ，     1 1 1 1 1 1 1 1FO FA AO BA AC OE OC CE AC CD3 2 3 2 6 2 2 3 1 1 1 1 .2 3 6 2                            － ， － 所以 m m n m n m n m m n FO OE  ，故 FO OE    FO  OE  3.设 =a, =b,直线AD,BE交于点G.设 =λ , =μ ,则 = + =(b-a)+μ =(b-a)+μ =b-a+μ =( μ-1)a+(1-μ)b, 又 =λ =λ( + )=λ = -λa+ λb,所以 解得 则 又因为 所以 所以G在中线CF上,所以AD,CF,BE相交于一点. CA  CB  AG  AD  BG  BE  AG  AB  BG  BE  1(BC CA)2   1( )2 a b 1 2 AG  AD  AC  CD  1( )2  a b 1 2 1 1,2 1 1 ,2         － － － 2 ,3 2.3     2 2 1 1 1CG CA AG AD ( ) .3 3 2 3 3             －a a a b a b 1 1CF 2 2   ，a b 2CG CF3   ， 【解题策略】 三点共线的证明 (1)平面上三点A,B,C共线⇔ =λ (向量共线且有公共点才能得出三点共 线). (2)点P为线段AB的中点,O为平面内任意一点⇔ . AB  BC  1OP (OA OB)2     (3)平面上三点A,B,C共线,O为不同于A,B,C的任意一点⇔ 且λ+μ=1. OC OA OB      类型二　证明等式、求值(逻辑推理、数学运算) 【典例】PQ过△OAB的重心G,且 求证: OP mOA OQ nOB.     ， 1 1 3.m n   【解题策略】 　向量法证明等式 向量法证明等式的关键是熟练掌握条件的向量等价表达式,常常借助三角形的 性质(例如:中线,重心等)及向量基本定理. 【跟踪训练】 如图,四边形ABCD是正方形,M是BC的中点,将正方形折叠,使点A与M重合,设折痕 为EF,若正方形面积为64,求△AEM的面积. 【解析】如图,建立坐标系,设E(e,0),AM交EF于点N,由正方形面积为64,可得边 长为8,由题意可得M(8,4),N是AM的中点,故N(4,2). 所以 因为 所以8(4-e)+4×2=0, 解得e=5,即AE=5,所以S△AEM= AE·BM=10. AM (8,4) EN AN AE (4,2) (e,0) (4 e,2)       ， － － － ， AM EN  ， 1 2 类型三　证明位置关系(逻辑推理) 　角度1　证明平行关系  【典例】证明顺次连接四边形各边中点所得四边形为平行四边形. 已知:如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点. 求证:四边形EFGH是平行四边形. 【思路导引】要证平行四边形,只需证一组对边平行且相等,即它们所对应的向 量相等. 【证明】连接AC.因为E,F分别是AB,BC的中点,所以 同理 所以 ,所以EF∥HG且EF=HG,所以四边形EFGH是平行四边形. 1 1 1 1EF EB BF AB BC (AB BC) AC2 2 2 2               ， 1HG AC2   ， EF HG  　角度2　证明垂直关系  【典例】证明直径所对的圆周角是直角. 已知:如图所示,已知☉O,AB为直径,C为☉O上任意一点. 求证:∠ACB=90°. 【思路导引】要证∠ACB=90°,只需证向量 ⊥ ,即 · =0. 【证明】连接CO,设 由此可得 即 · =0,即∠ACB=90°. AC  CB  AC  CB  AO OC AC CB        ， ，则 ， － ，a b a b a b   2 2 2 2 2 2AC CB ( ) | | r r 0.         － － －| | －a b a b a b a b AC  CB  【解题策略】 1.向量共线的相关结论 (1)a与b共线⇔a=λb(λ∈R,b≠0). (2)a=(x1,y1),b=(x2,y2),则a∥b⇔x1y2-x2y1=0. 2.向量垂直的相关结论 (1)数量积:a⊥b⇔a·b=0(a≠0,b≠0). (2)坐标表示:a=(x1,y1),b=(x2,y2),则a⊥b⇔x1x2+y1y2=0. 【题组训练】 1.若O为△ABC所在平面内一点,且满足( - )·( + -2 )=0,则△ABC 的形状为(　　) A.等腰三角形　　　　 B.直角三角形 C.正三角形 D.等腰直角三角形 OB  OC  OB  OC  OA  【解析】选A.因为 所以 所以 所以△ABC的中线和底边垂直,所以△ABC是等腰三角形. (OB OC) (OB OC 2OA) 0      － － ， CB (AB AC) 0     ， CB (AB AC)    ， 2.已知正方形ABCD,P为对角线AC上任意一点,PE⊥AB于点E,PF⊥BC于点F,连接 DP,EF.求证:DP⊥EF. 【证明】以A为原点,AB,AD所在直线分别为x轴,y轴建立直角坐标系. 设正方形边长为1,则 由已知,可设 并可得 因为 所以 ⊥ ,故DP⊥EF.    AB 1,0 AD 0,1 .   ， AP (a,a) ，  EB (1 a,0) BF 0,a EF (1 a,a) DP AP AD (a,a 1).          － ， ， － ， － － DP EF (a,a 1) (1 a,a) (1 a) a a (a 1) 0        － － － － ， DP  EF  3.在直角梯形ABCD中,AB∥CD,∠CDA=∠DAB=90°,CD=DA= AB. 求证:AC⊥BC. 1 2 【证明】如图,建立平面直角坐标系. 设CD=1,则A(0,0),B(2,0),C(1,1),D(0,1). 所以 =(-1,1), =(1,1), 所以 · =(-1,1)·(1,1)=-1+1=0, 所以 ⊥ ,即AC⊥BC. BC  AC  BC  AC  BC  AC  1.在△ABC中,若( + )·( - )=0,则△ABC(　　) A.是正三角形　　　　　　　　B.是直角三角形 C.是等腰三角形 D.形状无法确定 【解析】选C.因为 所以| |=| |,即CA=CB,故△ABC是等腰三角形. 课堂检测·素养达标 CA  CB  CA  CB  2 2 (CA CB) (CA CB) CA CB 0         － － ， CA  CB  2.在△ABC中,已知A(4,1),B(7,5),C(-4,7),则BC边上的中线AD的长是(　　) 【解析】选B.因为BC的中点为D , ,所以 . 5 5A.2 5 B. 2 7 5C.3 5 D. 2 3( ,6)2 5AD ( ,5)2  － 5 5AD 2  3.(教材二次开发:习题改编)在Rt△ABC中,斜边BC长为2,O是平面ABC外一点,点 P满足 则 等于(　　) A.2 B.1 C. D.4 1OP OA (AB AC)2       ， | AP |  1 2 【解析】选B.因为 所以 所以AP为Rt△ABC斜边BC的中线,所以| |=1. 1OP OA (AB AC)2       ， 1 1OP OA (AB AC) AP (AB AC)2 2           － ， ， AP  4.如图所示,在正方形ABCD中,E,F分别是AB,BC的中点. 求证:AF⊥DE. 【证明】如图,建立平面直角坐标系,设正方形的边长为2,则 A(0,0),D(0,2),E(1,0),F(2,1), =(2,1), =(1,-2). 因为 · =(2,1)·(1,-2)=2-2=0, 所以 ⊥ ,即AF⊥DE. AF  DE  AF  DE  AF  DE  二十六　向量在几何证明中的应用 【基础通关——水平一】 (15分钟　30分) 1.已知△ABC中, =a, =b,且a·b<0,则△ABC的形状为 (　　) A.钝角三角形　　　　　　 B.直角三角形 C.锐角三角形 D.等腰直角三角形 课时素养评价 AB  AC  【解析】选A.因为a·b= · =| |·| |cos A<0,所以A为钝角,故△ABC 为钝角三角形. AB  AC  AB  AC  2.在四边形ABCD中, = ,且| |=| |,那么四边形ABCD为(　　) A.平行四边形　　　　 B.菱形 C.长方形 D.正方形 【解析】选B.由 = 可知,该四边形为平行四边形,又由| |=| |知 邻边相等,故该四边形为菱形. AB  DC  AB  BC  AB  DC  AB  BC  3.△ABC顶点为A(a,0),B(-a,0),C(asin θ,acos θ),则△ABC为(　　) A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.等边三角形 【解析】选A.依题意可知a≠0, =(asin θ-a,acos θ), =(asin θ+a, acos θ), 与 不恒等,所以 · =(asin θ)2-a2+(acos θ)2 =a2(sin2θ+cos2θ)-a2=0,所以 ⊥ ,所以△ABC是直角三角形. BC  AC  | BC |  | AC |  BC  AC  BC AC  4.(2020·北京高考)已知正方形ABCD的边长为2,点P满足 = ( + ), 则| |=________; · =________.  【解析】如图建系,则A(0,0),B(2,0),C(2,2),D(0,2),所以 =(2,0), =(2,2), =(2,1),P(2,1), =(-2,1),| |= ,又 =(0,-1),所 以 · =-1. 答案: 　-1 AP  1 2 AB  AC  PD  PB  PD  AB  AC  AP  PD  5 PB  PB  PD  5 PD  5.在△ABC所在的平面内有一点P,如果 ,那么△PBC的面积与 △ABC的面积之比是________.  【解析】因为 所以 所以点P在边AC上,且3|PA|=|PC|,所以 ,如图, 设△ABC中AC边上的高为h,所以 答案: 2PA PC AB PB     － 2PA PC AB PB AB BP AP           － ， 2PA PC AP 3PA PC 0        － ， PC 3 AC 4  PBC ABC 1 PC h PCS 32 .1S AC 4AC h2       3 4 6.求证:以A(1,0),B(5,-2),C(8,4),D(4,6)为顶点的四边形是一个矩形. 【证明】因为 =(4,-2), =(3,6), =(4,-2), = , =(3,6) 不为零向量,且不与 平行,所以以A,B,C,D为顶点的四边形是平行四边形. 因为 · =0, ⊥ ,所以以A,B,C,D为顶点的四边形是矩形. AB  BC  DC  AB  DC  BC  AB  AB  BC  AB  BC  【能力进阶——水平二】 (30分钟　60分) 一、单选题(每小题5分,共20分) 1.若在△ABC中AB=AC=1,| + |= ,则△ABC的形状是 (　　) A.正三角形　　　　 B.锐角三角形 C.斜三角形 D.等腰直角三角形 AB  AC  2 【解析】选D.由| + |= , 得 ,因为AB=AC=1,所以 · =0,即AB⊥AC,所以 △ABC为等腰直角三角形. AB  AC  2 2 2 AB 2AB AC AC 2       AB  AC  【补偿训练】 已知非零向量 与 满足 且 则△ABC为(　　) A.等腰非等边三角形 B.直角三角形 C.等边三角形 D.三边均不相等的三角形 AB  AC  AB AC( ) BC 0 |AB| |AC|         ， | BC | 3|AB|  【解析】选A.不妨设 即 为∠BAC平分线所在直线上的向量, 又 ⊥ ,所以AB=AC,又 所以△ABC为等腰非等边三角形. AB ACAP |AB| |AC|      ， AP  AP  BC  | BC | 3 | AB| | AB|    2.已知△ABC为等腰三角形,满足AB=AC= ,BC=2,若P为底BC上的动点,则= (　　) A.有最大值8　　　　 B.是定值2 C.有最小值1 D.是定值4 3 AP (AB AC)    【解析】选D.设AD是等腰三角形的高,长度为 = .故 3 1 2 2 2 2AP (AB AC) (AD DP) 2AD 2AD 2DP AD 2AD 2 ( 2) 4.                     3.已知O是平面上一定点,满足 λ∈[0,+∞),则P 的轨迹一定通过△ABC的(　　) A.内心　　 B.垂心　　 C.重心　　 D.外心 AB ACOP OA ( ) |AB|cosB |AC|cosC         ， 【解析】选B.因为 所以 即 因为cos B= cos C= 所以 所以 垂直, 即 ⊥ ,所以点P在BC的高线上,即P的轨迹过△ABC的垂心. AB ACOP OA ( ) |AB|cos B |AC|cos C          ， AB ACOP OA ( ) |AB|cos B |AC|cos C        － ， AB ACAP ( ) |AB|cos B |AC|cos C        ， BA BC |BA||BC|     ， CA CB | CA||CB|     ， AB ACBC ( ) |BC| |BC| 0 |AB|cos B |AC|cos C           － ， AB ACBC ( ) |AB|cos B |AC|cos C      与 AP  BC  4.设a,b,c为同一平面内具有相同起点的任意三个非零向量,且a与b不共 线,a⊥c,|a|=|c|,则|b·c|的值一定等于(　　) A.以a,b为邻边的平行四边形的面积 B.以b,c为两边的三角形的面积 C.以a,b为两边的三角形的面积 D.以b,c为邻边的平行四边形的面积 【解析】选A.由题意可以画出图形:记 =a, =b, =c,=θ. 因为这三个向量的起点相同,且满足a与b不共线, a⊥c,|a|=|c|,利用向量的数量积定义,可得|b·c|= ||b|·|c|cos|=|OB|·|OC||cos θ|= |OB|·|OA|sin ∠AOB, 因为S△AOB= |OA|·|OB|sin∠AOB,所以|b·c|等于以a,b为邻边的平行四边形的 面积. OA  OB  OC  1 2 【误区警示】不作示意图,从而将角混淆. 二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错 的得0分) 5.在△ABC中,|AB|=2,|AC|=2 ,∠BAC=45°,P为线段AC上任意一点, 则 · 的可能值有 (　　) A.-2　　　 B.-1　　　 C.2　　　 D.3 2 PB  PC  【解析】选CD.设 因为 所以 因为0≤t≤1,所以- ≤ · ≤4,故2,3为可能取的值. PC tAC(0 t 1) AP (1 t)AC       ，则 － PB AB AP AB (1 t)AC,      － － － 2 2PB PC [AB (1 t)AC] tAC tAB AC t(1 t)AC 2 2 2t cos45 t( 1 t) (2 2)                － － － － － － 2 21 18t 4t 8(t )4 2  － － － ， 1 2 PB  PC  6.下列命题中正确的是 (　　) A.若向量a与b同向,且|a|>|b|,则a>b B.对于非零向量a,b,c,若a·(b-c)=0,则b=c C.已知A,B,C是平面内任意三点,则 D.若O为△ABC所在平面内任一点,且满足 则△ABC为等腰三角形 AB BC CA     0 (OB OC) (OB OC 2OA) 0      － － ， 【解析】选CD.选项A中,向量不能比较大小,故错误;选项B中,由a·(b-c)=0, 可得b=c或a⊥(b-c),故错误;选项C中, 故正确;选项D 中, 所以故△ABC为等腰三角形,正确. 【光速解题】本题中AB易判断错误,则可直接选CD. AB BC CA AC CA         ，0 2 2(OB OC) (OB OC 2OA) CB (AB AC) (AB AC) (AB AC) | AB| | AC | 0                      － － － － ， | AB| | AC |  ， 三、填空题(每小题5分,共10分) 7.点O是△ABC所在平面内的一点,满足 则点O是△ABC 的______心.  【解题指南】根据向量数量积的运算律可整理出 · =0,即OB⊥AC;同理 可得OA⊥BC,OC⊥AB,由垂心定义可知O为垂心. OA OB OB OC OC OA          ， OB  CA  【解析】因为 所以 即 · =0, 所以OB⊥AC,同理可得OA⊥BC,OC⊥AB, 所以点O为△ABC的垂心. 答案:垂 OA OB OB OC      ， (OA OC) OB 0   － ， OB  CA  【补偿训练】 过△ABC内一点M任作一条直线,再分别过顶点A,B,C作l的垂线,垂足分别为 D,E,F,若 恒成立,则点M是△ABC的________心.  【解析】本题采用特殊位置法较为简单. 因为过△ABC内一点M任作一条直线,可将此直线 特殊为过点A,则 =0,有 + =0. 如图,则有直线AM经过BC的中点,同理可得直线BM 经过AC的中点,直线CM经过AB的中点,所以点M是△ABC的重心. 答案:重 AD BE CF     0 AD  BE  CF  8.已知P是△ABC的边BC上任一点,且满足 ,x,y∈R,则 的最小值是____.  【解析】因为点P落在△ABC的边BC上,所以B,P,C三点共线,所以x+y=1.故 当且仅当 即x= ,y= 时取等号, 所以 的最小值为9. 答案:9 AP xAB yAC    1 4 x y  1 4 1 4 y 4x+ =( + )(x+y)= + +5 4+5=9,x y x y x y  y 4x x y  ， 1 3 2 3 1 4 x y  四、解答题(每小题10分,共20分) 9.如图,已知直角梯形ABCD中,AD⊥AB,AB=2AD=2CD,过点C作CE⊥AB于点E,M为 CE的中点. 求证:(1)DE∥BC;(2)D,M,B三点共线. 【证明】以E为原点,AB所在直线为x轴,EC所在直线为y轴建立平面直角坐标系, 如图.令| |=1,则| |=1,| |=2,因为CE⊥AB,AD=DC,所以四边形AECD为 正方形,所以各点坐标分别为E(0,0),B(1,0),C(0,1),D(-1,1),A(-1,0). AD  CD  AB  (1)因为 =(-1,1)-(0,0)=(-1,1), =(0,1)-(1,0)=(-1,1),所以 = ,即DE∥BC. (2)因为M为EC的中点,所以M(0, ),所以 =(-1,1)-(0, )=(-1, ), =(1,0)-(0, )=(1,- ),所以 =- ,所以 ∥ . 又 与 有公共点,所以D,M,B三点共线. ED  BC  ED  BC  1 2 1 2 1 2 1 2 1 2 MD  MB  MD  MB  MD  MB  MD  MB  10.四边形ABCD中, =a, =b, =c, =d,且a·b=b·c=c·d=d·a, 试问四边形ABCD是什么图形? 【解析】因为a·b=b·c,所以b·(a-c)=0,即b⊥(a-c).同理d⊥(a-c),所以b∥d,同 理a∥c,所以四边形ABCD是平行四边形.所以a=-c,故b·(a-c)=b·2a=0,所以a·b=0, 故该四边形为矩形. BC AB  CD  DA  【创新迁移】 在△ABC所在平面内有一点H满足  则H点是△ABC的________.  【解析】因为 所以 整理得 即AB⊥HC;同理可得AC⊥HB,BC⊥HA. 所以可知H为垂心. 答案:垂心 2 2 2 2 2 2 HA BC HB CA HC AB ,          BC HC HB,CA HA HC,AB HB HA           － － － ， 2 22 2HA (HC HB) HB (HA HC)        － － ， HC (HB HA) 0,HC AB 0,       － 【补偿训练】 设P,Q分别是梯形ABCD的对角线AC与BD的中点.(1)试用向量证明:PQ∥AB; (2)若AB=3CD,求PQ∶AB的值. 【解析】(1)因为Q为BD中点,所以 又因为P为AC中点,所以 所以 又向量 与 共线,设向量 则 CB CD 2CQ    ， CA 2CP  ； 2PQ 2CQ 2CP (CB CD) CA CB CD AC AB CD.                   － － CD  AB  CD AB   ， 2PQ (1 )AB    ， 所以 又梯形ABCD中, 所以λ≠-1, 所以 ∥ ,即PQ∥AB. (2)因为向量 与 反向,且 所以 即λ=- ,代入①式,得 所以PQ∶AB=1∶3. 1PQ AB.2    ① | AB| | CD |  ， PQ  AB  AB  CD  | AB| 3|CD|,  AB 3CD  － ， 1 3 11 13PQ AB AB2 3    － ，