高中数学（人教A版）必修4：2-3-1同步试题（含详解） 7页

高中数学(人教A版)必修4同步试题 ‎1．给出下面三种说法：‎ ‎①一个平面内只有一对不共线的非零向量可作为表示该平面所有向量的基底；‎ ‎②一个平面内有无数多对不共线的非零向量可作为表示该平面所有向量的基底；‎ ‎③零向量不可为基底中的向量．‎ 其中正确的说法是(　　)‎ A．①②　　　　　　　　 B．②③‎ C．①③ D．②‎ 解析　因为不共线的两个向量都可以作为一组基底，所以一个平面内有无数多个基底，又零向量和任何向量共线，所以基底中不含有零向量．因此本题中，①错，②、③正确，故选B.‎ 答案　B ‎2．已知e1和e2是表示平面内所有向量的一组基底，那么下面四组向量中不能作为一组基底的是(　　)‎ A．e1和e1＋e2‎ B．e1－2e2和e2－2e1‎ C．e1－2e2和4e2－2e1‎ D．e1＋e2和e1－e2‎ 解析　分析四个选项知，在C中，4e2－2e1＝－2(e1－2e2)．∴e1－2e2与4e2－2e1共线，应选C.‎ 答案　C ‎3．在△ABC中，＝3，则等于(　　)‎ A.(＋2)‎ B.(＋2)‎ C.(＋3)‎ D.(＋2)‎ 解析　如右图所示，‎ ＝＋ ‎＝＋ ‎＝＋(－)‎ ‎＝＋＝(＋2)，故选A.‎ 答案　A ‎4．已知四边形ABCD是菱形，点P在对角线AC上(不包括端点A，C)，则等于(　　)‎ A．λ(＋)，λ∈(0,1)‎ B．λ(＋)，λ∈ C．λ(－)，λ∈(0,1)‎ D．λ(－)，λ∈ 解析　∵ABCD是菱形，且AC是一条对角线，由向量的平行四边形法则知，＝＋，而点P在AC上，‎ ‎∴三点A，P，C共线，∴＝λ＝λ(＋)，显然λ∈(0,1)，故选A.‎ 答案　A ‎5．若四边形ABCD为正方形，E是CD的中点，且＝a，＝b，则等于(　　)‎ A．b＋a B．b－a C．a＋b D．a－b 解析　＝＋＝＋＝b－a.‎ 答案　B ‎6．已知a，b不共线，且c＝λ‎1a＋λ2b(λ1，λ2∈R)，若c与b共线，则λ1＝________.‎ 解析　∵a，b不共线，∴a，b可以作为一组基底，又c与b共线，∴c＝λ2b，∴λ1＝0.‎ 答案　0‎ ‎7．设向量a，b不共线，且＝k‎1a＋k2b，＝h‎1a＋h2b，若＋＝ma＋nb，则实数m＝________，n＝________.‎ 解析　＋＝(k1＋h1)a＋(k2＋h2)b＝ma＋nb.‎ ‎∴m＝k1＋h1，n＝k2＋h2.‎ 答案　k1＋h1　k2＋h2‎ ‎8．已知向量a与b的夹角是45°，则－‎2a与3b的夹角是________．‎ 答案　135°‎ ‎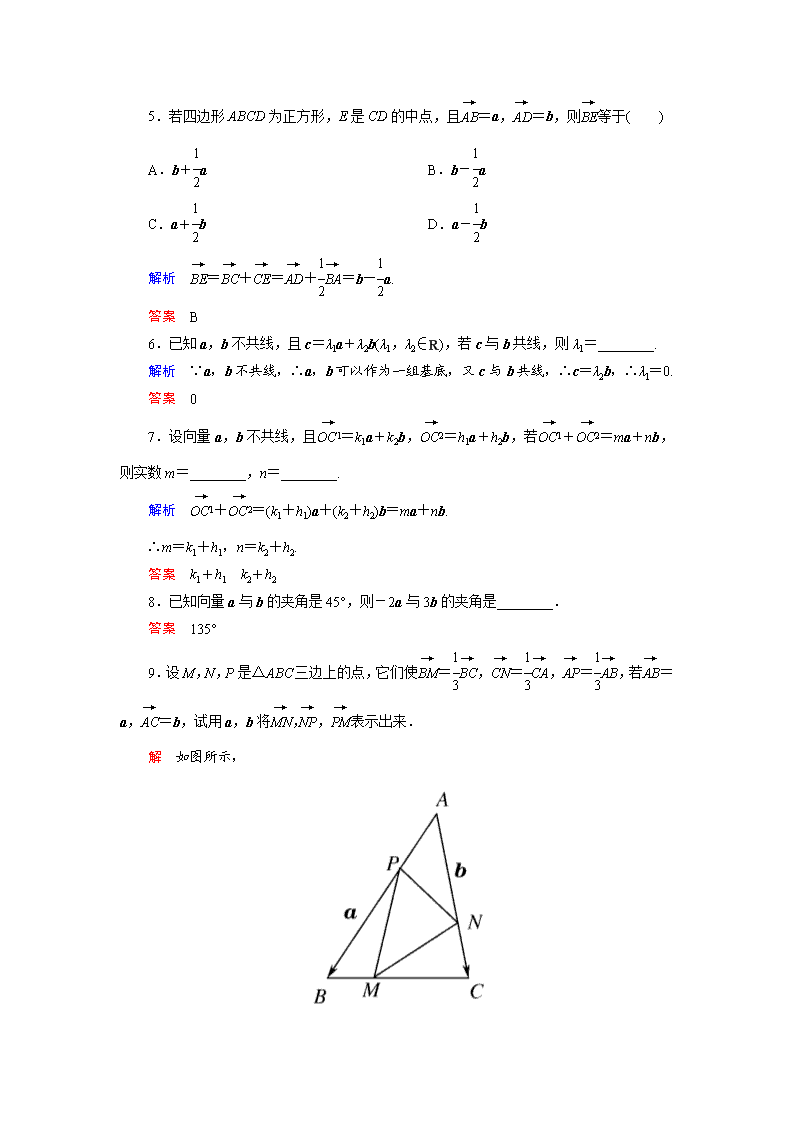9．设M，N，P是△ABC三边上的点，它们使＝，＝，＝，若＝a，＝b，试用a，b将，，表示出来．‎ 解　如图所示，‎ ＝－＝－－ ‎＝－－(－)‎ ‎＝－＝b－a.‎ 同理可得＝a－b，‎ ＝－＝－(＋)＝a＋b.‎ ‎10．如图所示，在▱ABCD中，M，N分别为DC，BC的中点．已知＝c，＝d，试用c，d表示和.‎ 解　设＝a，＝b.‎ 由M，N分别为DC，BC的中点，得＝b，＝a.‎ 在△ABN和△ADM中，‎ ‎①×2－②，得a＝(2d－c)．‎ ‎②×2－①，得b＝(‎2c－d)．‎ ‎∴＝(2d－c)，＝(‎2c－d).‎ 教师备课资源 ‎1.已知向量a＝e1－2e2，b＝2e1＋e2，其中e1，e2不共线，则a＋b与c＝6e1－2e2的关系为(　　)‎ A．不共线 B．共线 C．相等 D．不能确定 解析　a＋b＝3e1－e2＝c.故a＋b与c共线．‎ 答案　B ‎2．设平面向量a1，a2，a3的和a1＋a2＋a3＝0.如果平面向量b1，b2，b3满足|bi|＝2|ai ‎|，且ai顺时针旋转30°后与bi同向，其中i＝1,2,3，那么(　　)‎ A．－b1＋b2＋b3＝0 B．b1－b2＋b3＝0‎ C．b1＋b2－b3＝0 D．b1＋b2＋b3＝0‎ 解析　选用特例法 ‎∵a1＋a2＋a3＝0，‎ ‎∴a1，a2，a3构成三角形，不妨设其为正三角形．则bi实际上是将三角形顺时针旋转30°后再将其各边长度变为原来的2倍，仍为封闭图形——三角形．‎ ‎∴有b1＋b2＋b3＝0.‎ 答案　D ‎3．已知＝a＋2b，＝－‎4a－b，＝－‎5a－3b，试判断A，B，C，D四点构成的图形．‎ 解　∵＝＋＋＝－‎8a－2b，‎ ‎∴＝2，∴∥.‎ 若A，B，C三点共线，则存在实数λ，使＝λ，‎ 即a＋2b＝－4λa－λb，∴矛盾．‎ ‎∴A，B，C三点不共线，故A，B，C，D四点不共线．‎ 因而∥，又||＝2||≠||.‎ 故A，B，C，D四点构成梯形．‎ ‎4．已知：如图，点L，M，N分别为△ABC的边BC，CA，AB上的点，且＝l，＝m，＝n，若＋＋＝0.求证：l＝m＝n.‎ 证明　设＝a，＝b为基底．‎ 由已知＝la，＝mb.‎ ‎∵＝＋＝－a－b，‎ ‎∴＝n＝－na－nb.‎ ‎∴＝＋＝(l－1)a－b，①‎ ＝＋＝a＋mb，②‎ ＝＋＝－na＋(1－n)b.③‎ 将①②③代入＋＋＝0，得 ‎(l－n)a＋(m－n)b＝0，‎ ‎∵a与b不共线，‎ ‎∴l＝m＝n.‎ ‎5.‎ 在△ABC中，＝，DE∥BC，与边AC相交于点E，△ABC的中线AM与DE相交于点N，如图所示，设＝a，＝b，试用a和b表示.‎ 解　∵M为BC的中点，‎ ‎∴＝＝(－)＝(b－a)，‎ ＝(＋)＝(a＋b)．‎ ‎∵∥，与共线，‎ ‎∴存在实数λ和μ，使得＝λ＝λ(b－a)，‎ ＝μ＝μ(a＋b)＝μa＋μb.‎ ＝＋ ‎＝a＋λ(b－a)＝a＋b.‎ 根据平面向量基本定理，得 解得　λ＝μ＝.∴＝(b－a)．‎