高中数学选修2-2课件数学：3_3_1《数系的扩充与复数的概念》课件（人教A版选修2-2） 10页

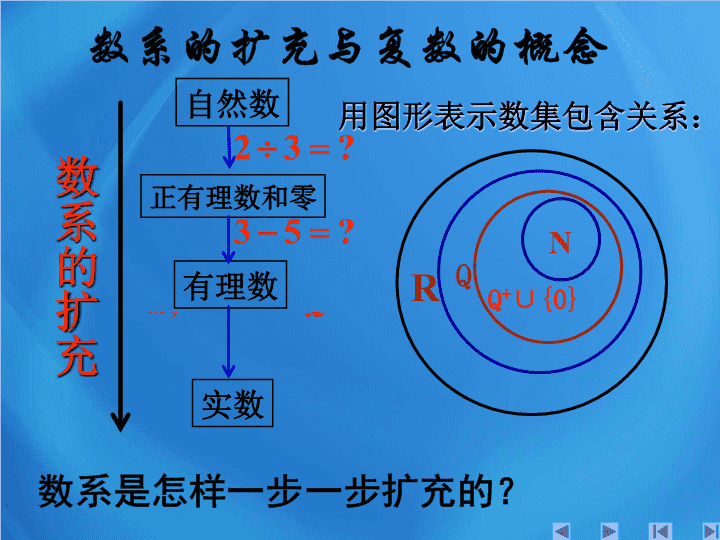
数系的扩充 自然数 正有理数和零 有理数 实数 N Q + ∪{0} Q R 用图形表示数集包含关系： 大胆假设 例题 1 与练习 1 回顾数系扩充 问题提出 代数形式 虚数 发展史 为了解决负数开平方问题， 数学家大胆引入 一个新数 i ，把 i 叫做虚数单位，并且规定： (1) i 2  1 ； (2) 实数可以与 i 进行四则运算 , 在进行四则运算时 , 原有的加法与乘法的运算律 ( 包括交换律、结合律和分配律 ) 仍然成立 . 问题解决 : 其中 a — 实部 , b — 虚部 , 复数的代数形式： 通常用字母 z 表示，即 称为 虚数单位 . 讨论 : 复数集 C 和实数集 R 之间有什么关系？ 规定 : 0 i = 0 ,0+ bi = bi, a +0 i = a 例 1 实数 m 取什么值时，复数 是（ 1 ）实数？ （ 2 ）虚数？ （ 3 ）纯虚数？ 解 : （ 1 ） 当 ，即 时，复数 z 是实数． （ 2 ） 当 ，即 时，复数 z 是虚数． （ 3 ） 当 即 时，复数 z 是 纯虚数． 练习 1: 当 m 为何实数时，复数 是 （ 1 ）实数 （ 2 ）虚数 （ 3 ）纯虚数 练习 2 2 答案 如果两个复数的 实部 和 虚部 分别相等，那么我们就说这两个 复数相等 ． 例 2 已知 ，其中 求 解：根据复数相等的定义，得方程组 解得 如果两个复数的 实部 和 虚部 分别相等，那么我们就说这两个 复数相等 ． 1. 虚数单位 i 的引入； 2. 复数有关概念： 复数的代数形式 : 复数的实部 、虚部 复数相等 虚数、纯虚数 3. 复数的分类： 学习小结