数学理卷·2019届山西省太原五中高二10月月考（2017-10） 6页

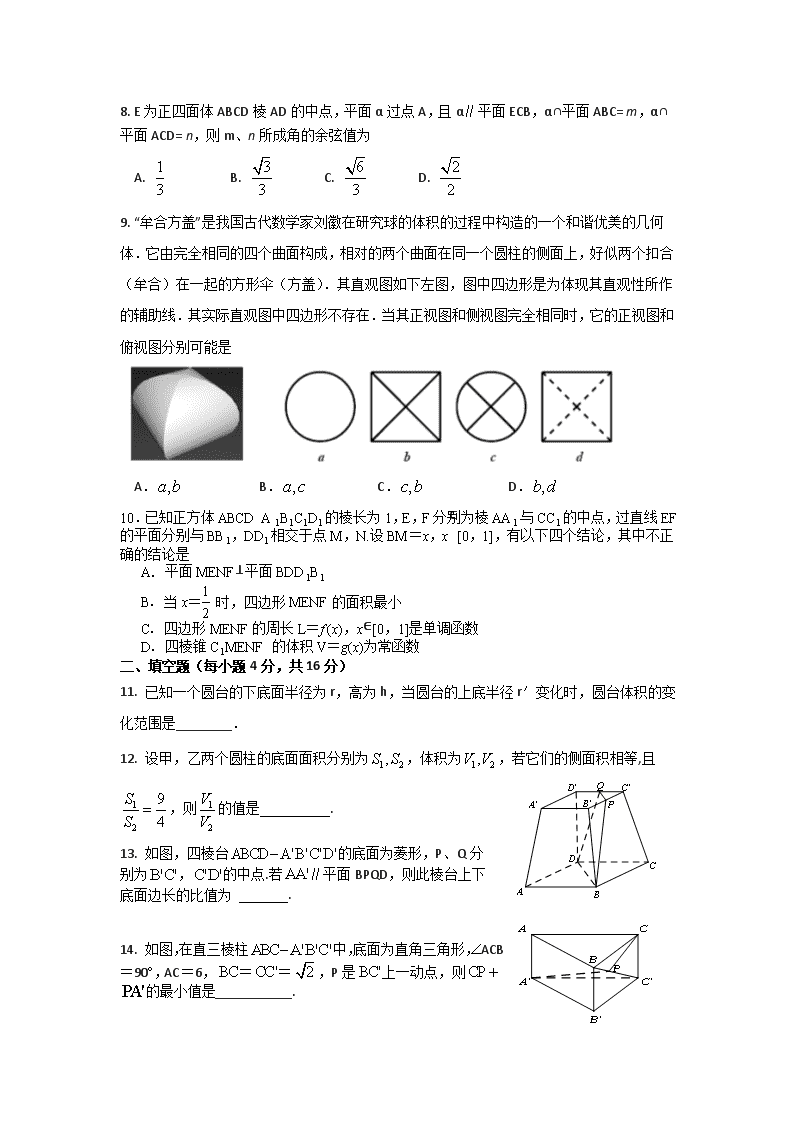
太原五中2017-2018学年度第一学期阶段性检测 高 二 数 学(理)‎ 出题人、校对人：张福兰 李小丽 王琪（2017年10月）‎ 一、选择题（每小题4分,共40分,每小题只有一个正确答案）‎ ‎1. 若一个圆锥的轴截面是等边三角形，其面积为，则这个圆锥的全面积为 A . 3 B. 3 C . 6 D. 9‎ ‎ 2.已知是两条不同直线，是三个不同平面，下列命题中正确的是 A. 若，则 B. 若，则 ‎ C. 若，则 D. 若，则 ‎3. 如图，格纸上小正方形的边长为1，用粗实线画出某几何体的三视图，则该几何体的体积为 A． B． C． D．‎ ‎4. 设是空间四个不同的点，在下列命题中，不正确的是 A．若与共面,则与共面 B．若与是异面直线,则与是异面直线 C．若,,则 D．若,,则 ‎5. 正四棱锥的体积为，底面对角线的长为，则侧面与底面所成的二面角的正切值等于 A． B． C． D．‎ ‎6. 《九章算术》是我国古代数学名著，它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形，且侧棱垂直于底面的三棱柱；阳马指底面为矩形，一侧棱垂直于底面的四棱锥.如图，在堑堵ABC-A1B1C1中，AC⊥BC，若A1A=AB=2 ，当阳马B-A1ACC1体积最大时，则堑堵ABC-A1B1C1的体积为 A. B. C. D. ‎7. 已知某几何体的三视图如右图所示，则该几何体的外接球表面积为 A. B. ‎32‎ C. D. ‎ ‎8. E为正四面体ABCD棱AD的中点，平面α过点A，且α∥平面ECB，α∩平面ABC= m，α∩平面ACD= n，则m、n所成角的余弦值为 A. B. C. D. ‎ ‎9. “牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体．它由完全相同的四个曲面构成，相对的两个曲面在同一个圆柱的侧面上，好似两个扣合（牟合）在一起的方形伞（方盖）．其直观图如下左图，图中四边形是为体现其直观性所作的辅助线．其实际直观图中四边形不存在．当其正视图和侧视图完全相同时，它的正视图和俯视图分别可能是 A． B． C． D．‎ ‎10．已知正方体ABCD A1B‎1C1D1的棱长为1，E，F分别为棱AA1与CC1的中点，过直线EF的平面分别与BB1，DD1相交于点M，N.设BM＝x，x∈[0，1]，有以下四个结论，其中不正确的结论是 A. 平面MENF⊥平面BDD1B1‎ B. 当x＝ 时，四边形MENF的面积最小 C. 四边形MENF的周长L＝f (x)，x∈[0，1]是单调函数 D. 四棱锥C1MENF的体积V＝g(x)为常函数 二、填空题（每小题4分，共16分）‎ ‎11. 已知一个圆台的下底面半径为r，高为h，当圆台的上底半径r′变化时，圆台体积的变化范围是________．‎ ‎12. 设甲，乙两个圆柱的底面面积分别为，体积为，若它们的侧面积相等,且，则的值是 . ‎ ‎13. 如图，四棱台的底面为菱形，P、Q分 别为，的中点.若∥平面BPQD，则此棱台上下 底面边长的比值为 .‎ ‎14. 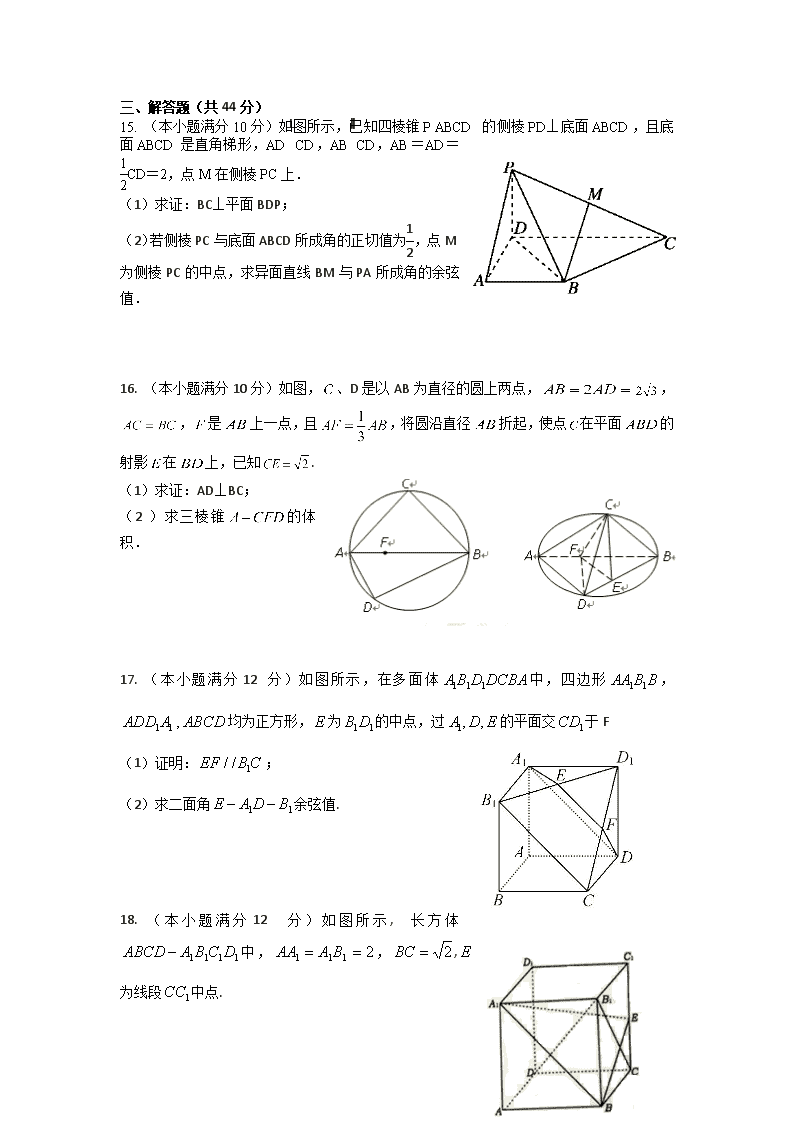如图，在直三棱柱中，底面为直角三角形，ÐACB＝90°，AC＝6，＝＝，P是上一动点，则＋的最小值是___________.‎ 三、解答题（共44分）‎ ‎15. （本小题满分10分）如图所示，已知四棱锥P ABCD的侧棱PD⊥底面ABCD，且底面ABCD是直角梯形，AD⊥CD，AB∥CD，AB＝AD＝CD＝2，点M在侧棱PC上．‎ ‎（1）求证：BC⊥平面BDP；‎ ‎（2）若侧棱PC与底面ABCD所成角的正切值为，点M为侧棱PC的中点，求异面直线BM与PA所成角的余弦值．‎ ‎16. （本小题满分10分）如图，、D是以AB为直径的圆上两点，，，是上一点，且，将圆沿直径折起，使点在平面的射影在上，已知.‎ ‎（1）求证：AD⊥BC；‎ ‎（2）求三棱锥的体积．‎ ‎17.（本小题满分12分）如图所示，在多面体中，四边形，均为正方形，为的中点，过的平面交于F ‎（1）证明：；‎ ‎（2）求二面角余弦值.‎ ‎18. （本小题满分12分）如图所示,长方体中，，,为线段中点.‎ ‎（1）求证：平面⊥平面；‎ ‎（2）若点为侧面（包含边界）内的一个动点，且平面,求线段长度的最小值.‎ 太原五中2017-2018学年度第一学期月考 高 二 数 学(理科)答案 一、选择题（每小题4分,共40分,每小题只有一个正确答案）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 A A D D B C C B A C 二、填空题（每小题4分，共16分）‎ ‎11.；12.；13.；14.；‎ 三、解答题（共44分）‎ ‎15．解：(1)证明：由已知可得BD＝BC＝2 ，∴BD2＋BC2＝16＝DC2，故BD⊥BC.‎ 又PD⊥平面ABCD，BC⊂平面ABCD，故PD⊥BC，‎ 又BD∩PD＝D，∴BC⊥平面BDP.‎ ‎(2)如图，取PD的中点N，并连接AN，MN，‎ BM∥AN，则∠PAN即为异面直线BM与PA所成的角．‎ 又PD⊥底面ABCD，∴∠PCD即为PC与底面ABCD所成的角，‎ 即tan∠PCD＝，∴PD＝CD＝2，即PN＝PD＝1，‎ AN＝，PA＝2 ，则在△PAN中，cos∠PAN＝＝，‎ 即异面直线BM与PA所成角的余弦值为.‎ ‎16. （1）证明：依题，平面 ∴‎ · ‎ ∴平面 ∴AD⊥BC ……5分 ‎（2）解： 到的距离等于∴．‎ · 平面 ‎∴． ‎ ‎17.解：（1）因为平面,平面，所以平面,又平面，平面平面=EF，所以EF//.‎ ‎(2)将几何体补成正方体知，BD1⊥平面，所以BD1⊥A1D ‎ AD1⊥平面，所以AD1⊥A1D，所以交线A1D⊥平面ABD1.二面角的平面角与∠AD1B相等，余弦值为 ‎ ‎18. 解：（Ⅰ）在长方体中，⊥平面 ‎∴‎ 又∵为线段的中点，由已知易得∽‎ ‎∴，∴,‎ 故，且，∴⊥平面 又平面，∴平面⊥平面 ‎（2）取线段A1B1的中点M，线段BB1的中点N，连接C1M，C1N，MN，则 C1N∥BE，MN∥A1B.‎ 又∵MN∩C1N=N，BA1∩BE=B，‎ ‎∴平面C1MN∥平面A1BE.‎ 要使得线段C1P长度最小，则C1P⊥MN,在⊿C1MN中，C1M=C1N= MN=，则C1P=‎