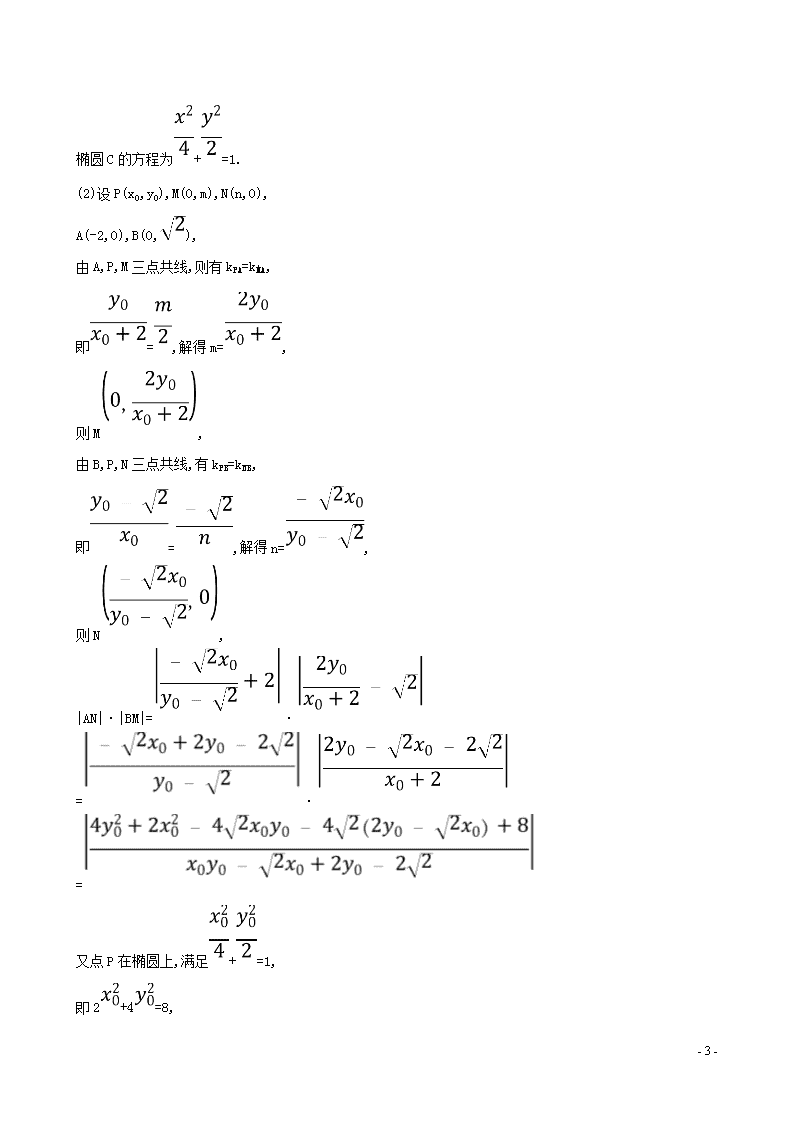2021版高考数学一轮复习核心素养测评六十三圆锥曲线中的定值与定点问题理北师大版 4页

核心素养测评六十三 圆锥曲线中的定值与定点问题 1. ‎(2020·北京模拟)已知椭圆C:+y2=1(a>1)的离心率为. ‎ ‎(1)求椭圆C的方程.‎ ‎(2)设直线l过点M(1,0)且与椭圆C相交于A,B两点.过点A作直线x=3的垂线,垂足为D.证明直线BD过x轴上的定点.‎ ‎【解析】(1)由题意可得, 解得a=,b=1,‎ 所以椭圆C的方程为+y2=1 .‎ ‎(2)直线BD恒过x轴上的定点(2,0).证明如下:‎ ‎①当直线l斜率不存在时,直线l的方程为x=1,‎ 不妨设A,B,D.‎ 此时,直线BD的方程为:y=(x-2),所以直线BD过定点(2,0).‎ ‎②当直线l的斜率存在时,设A(x1,y1),B(x2,y2),直线AB的方程为y=k(x-1),D(3,y1).‎ 由,得:(1+3k2)x2-6k2x+3k2-3=0.‎ 所以x1+x2=,x1x2=.……(*)‎ 直线BD的方程为:y-y1=(x-3),只需证明直线BD过点(2,0)即可.‎ - 4 -‎ 令y=0,得x-3=-,‎ 所以x==‎ ‎=‎ 即证=2,即证2-x1x2=3.‎ 将(*)代入可得2-x1x2=-==3.‎ 所以直线BD过点(2,0),‎ 综上所述,直线BD恒过x轴上的定点(2,0).‎ ‎2.(2020·上饶模拟)已知椭圆C:+=1(a>b>0),离心率e=,点G(,1)在椭圆上. ‎ ‎(1)求椭圆C的标准方程.‎ ‎(2)设点P是椭圆C上一点,左顶点为A,上顶点为B,直线PA与y轴交于点M,直线PB与x轴交于点N,求证:|AN|·|BM|为定值.‎ ‎【解析】(1)依题意得=,设c=t,则a=2t,b=t,‎ 由点G(,1)在椭圆上,有+=1,解得t=1,则a=2,b=,‎ - 4 -‎ 椭圆C的方程为+=1.‎ ‎(2)设P(x0,y0),M(0,m),N(n,0),‎ A(-2,0),B(0,),‎ 由A,P,M三点共线,则有kPA=kMA,‎ 即=,解得m=,‎ 则M,‎ 由B,P,N三点共线,有kPB=kNB,‎ 即=,解得n=,‎ 则N,‎ ‎|AN|·|BM|=·‎ ‎=·‎ ‎=‎ 又点P在椭圆上,满足+=1,‎ 即2+4=8,‎ - 4 -‎ 代入上式得 ‎|AN|·|BM|=‎ ‎==4,‎ 可知|AN|·|BM|为定值4.‎ - 4 -‎