2017-2018学年贵州省铜仁市西片区高中教育联盟高二下学期期末考试数学（文）试题-解析版 16页

绝密★启用前 贵州省铜仁市西片区高中教育联盟 2017-2018 学年高二下学 期期末考试数学（文）试题 评卷人 得分 一、单选题 1．已知全集 ，若 ， ，则 等于( ) A. B. C. D. 【答案】D 【解析】根据题意得到 ， = ，故得到 = . 故答案为：D. 2．若复数 (其中 为虚数单位)在复平面中对应的点位于( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 【答案】D 【解析】分析：利用复数的出发计算得到 ，即可得到结论. 详解： 故 在复平面中对应的点位于第四象限. 故选 D. 点睛：本题考查复数乘法运算及复数的几何意义，是基础题. 3．若双曲线 的焦距为 ，则实数 为( ) A. 2 B. 4 C. D. 【答案】A 【解析】双曲线 的焦距为 故答案为：A. 4．某公司某件产品的定价 与销量 之间的统计数据表如下，根据数据，用最小二乘法 得出 与 的线性回归直线方程为 ，则表格中 的值为( ) { }1,2,3,4U = { }1,3A = { }3B = ( ) ( )U UC A C B∩ { }1,2 { }1,4 { }2,3 { }2,4 { }2,4UC A = UC B { }1,2,4 ( ) ( )U UC A C B∩ { }2,4 2 2 2: 1( 0)6 x yC aa − = > 2 10 a 5 2 2 2 2: 1( 0)6 x yC aa − = > 22 6 2 10 2.a a+ = ⇒ = 1 3 4 5 7 10 20 35 45 A. 25 B. 30 C. 40 D. 45 【答案】C 【解析】 ，所以 ，得 故选：C． 5．已知 ， ， ， ，从 以上四个函数中任意取两个相乘得到新函数，那么所得新函数为奇函数的概率为( ) A. B. C. D. 【答案】C 【解析】两个奇函数相乘为奇函数，两个偶函数相乘为偶函数，一个奇函数一个偶函数 相乘得到奇函数. ， ， ，为奇函数， 为偶函数，任意两个相乘得到的函数个数有 6 种，得到奇函数的个数为 3 个，故概率为 故答案为：C. 6．设 是周期为 4 的奇函数，当 时， ，则 ( ) A. B. C. D. 【答案】D 【解析】 因为函数 是周期为 的奇函数，当 时， ， 所以 ，故选 D. 7．某几何体由上、下两部分组成，其三视图如图所示，其俯视图是由一个半圆与其直 径组成的图形，则该几何体上部分与下部分的体积之比为( ) ( )1f x x= ( )2 sinf x x= ( )3 cosf x x= ( ) ( )2 4 lg 1f x x x= + + 1 4 1 3 1 2 2 3 ( )1f x x= ( )2 sinf x x= ( ) ( )2 4 lg 1f x x x= + + ( )3 cosf x x= 3 1 .6 2 = A. B. C. D. 【答案】C 【解析】根据题意得到原图是半个圆锥和半个圆柱构成的图形，圆锥的地面半径为 2， 圆 柱 底 面 半 径 为 2 ， 故 得 到 圆 锥 的 体 积 为 ， 半 个 圆 柱 的 体 积 为 该几何体上部分与下部分的体积之比为 . 故答案为：C. 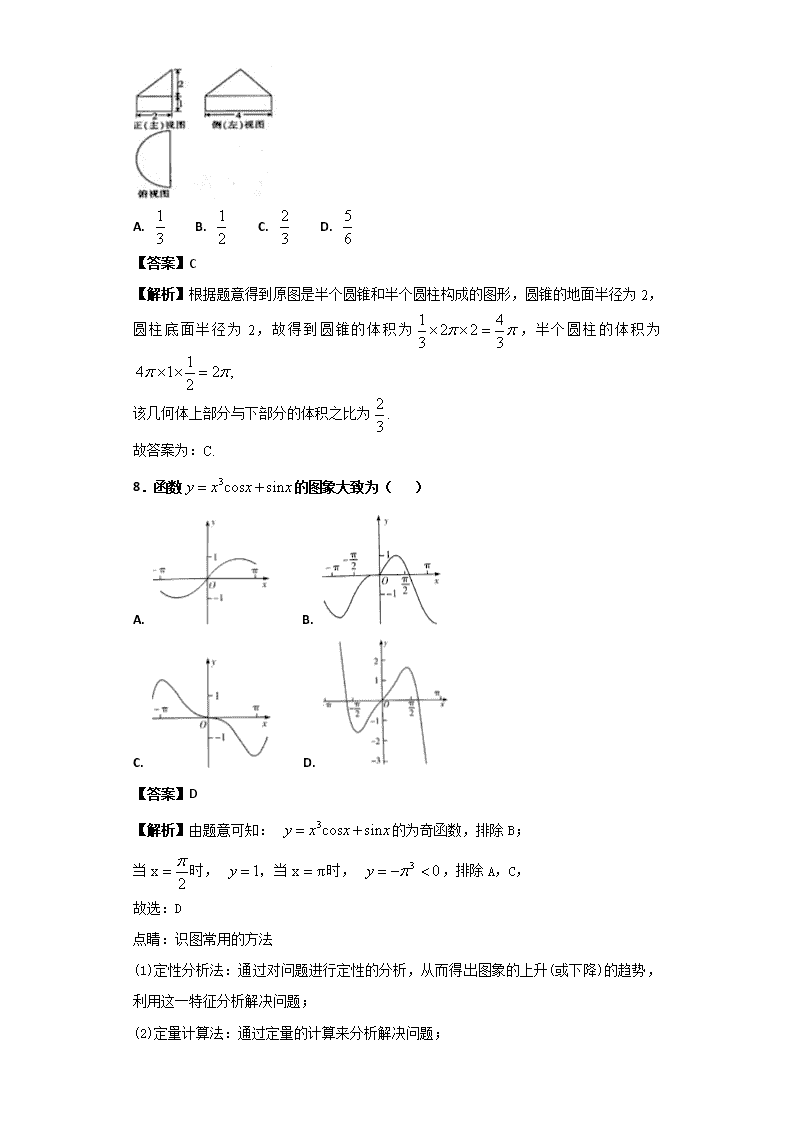8．函数 的图象大致为（ ） A. B. C. D. 【答案】D 【解析】由题意可知： 的为奇函数，排除 B； 当 时， ，当 时， ，排除 A，C， 故选：D 点睛：识图常用的方法 (1)定性分析法：通过对问题进行定性的分析，从而得出图象的上升(或下降)的趋势， 利用这一特征分析解决问题； (2)定量计算法：通过定量的计算来分析解决问题； 1 3 1 2 2 3 5 6 1 42 23 3 π π× × = 14 1 2 ,2 π π× × = 2 3 3cos siny x x x= + 3cos siny x x x= + x 2 π= 1y = x π= 3 0y π= − < (3)函数模型法：由所提供的图象特征，联想相关函数模型，利用这一函数模型来分析 解决问题． 9．已知函数 ，若 ， 的图象恒在直线 的上 方，则 的取值范围是( ) A. B. C. D. 【答案】C 【解析】分析：根据函数 的解析式，利用 的取值范围，结合题意求出 的取值范 围． 详 解 ： 函 数 函 数 ， 时 ， 又 的 图 象 恒 在 直 线 的 上 方 ， 解得 ； ∴ 的取值范围是 ． 故选：C． 点睛：本题考查了三角函数的图象与性质的应用问题，是基础题． 10．有编号依次为 1，2，3，4，5，6 的 6 名学生参加数学竞赛选拔赛，今有甲、乙、 丙、丁四位老师在猜谁将得第一名，甲猜不是 3 号就是 5 号；乙猜 6 号不可能；丙猜 2 号，3 号，4 号都不可能；丁猜是 1 号，2 号，4 号中的某一个.若以上四位老师中只有 一位老师猜驿，则猜对者是( ) A. 甲 B. 乙 C. 丙 D. 丁 【答案】C 【解析】若甲猜对，则乙也猜对，故不满足题意；若乙猜对则丁也可能猜对，故不正确； 若丁猜对，则乙也猜对，故也不满足条件.而如果丙猜对，其他老师都不会对. 故答案为：C. 11．抛物线 的焦点为 ，准线为 是 上一点，连接 并延长交抛物线 于点 ， 若 ，则 ( ) A. 3 B. 4 C. 5 D. 6 【答案】C 【解析】 设 Q 到 l 的距离为 d，则由抛物线的定义可得，|QF|=d， ∵|PF|= |PQ|，∴ ∴直线 PF 的斜率为 ， ∵F（2，0），∴直线 PF 的方程为 y=﹣2 （x﹣2）， 与 y2=8x 联立可得 x=3，（由于 Q 的横坐标大于 2） ∴|QF|=d=3+2=5， 故选：C 12．已知函数 ，若有且仅有一个整数 ，使得 ，则实数 的取值范围 是( ) A. B. C. D. 【答案】B 【解析】函数 ，若有且仅有一个整数 ，使得 ，不等式程 只有一个整数解，在同一坐标系中画出图像，可知这个整数解就是 3 ，故得到 ，解得不等式组解集为 . 故答案为： . 点睛：本题中涉及根据函数零点个数求参数取值，是高考经常涉及的重点问题，（1）利 用零点存在的判定定理构建不等式求解；（2）分离参数后转化为函数的值域（最值） 问题求解，如果涉及由几个零点时，还需考虑函数的图象与参数的交点个数；（3）转 化为两熟悉的函数图象的上、下关系问题，从而构建不等式求解. 第 II 卷（非选择题） 请点击修改第 II 卷的文字说明 评卷人 得分 二、填空题 13．已知 ， ， ，若 ，则实数 ______________. 【答案】7 【 解 析 】 根 据 题 意 得 到 - = 故答案为：7. 14．已知变量 ， 满足约束条件 ，则 的最大值为 ______________. 【答案】6 【解析】根据不等式组画出可行域是一个封闭的三角形区域，目标函数可化简为 截距越大目标函数值越大，故当目标函数过点 时，取得最大值，代入得到 6. 故答案为：6. 15．在 中，若 ，则 __________． 【答案】 【解析】由正弦定理可得： ， 不妨设 ， 则 . 16．已知数列 满足： ，数列 的前 项和为 ，则 ___________. ( )3, 2a m= − ( )1,2b m= − ( )2,1c = − ( )a c b− ⊥   m = a c ( ) ( ) ( )5, 2 1 , 1,2 , · 7 0 7.m b m a c b m m− − = − − = − = ⇒ =   x y 1 0 { 1 0 1 x y x y y − − ≤ + + ≥ ≤ 2 1z x y= + + 2 1y x z= − + − ( )2,1 【答案】 【解析】由 ①，得 ② ， ① ② 得 ， 即 ， 所 以 数 列 的 通 项 ，所以 故答案为： 点睛：裂项抵消法是一种常见的求和方法，其适用题型主要有： （1）已知数列的通项公式为 ，求前 项和： ； （2）已知数列的通项公式为 ，求前 项和： ； （3）已知数列的通项公式为 ，求前 项和:. 评卷人 得分 三、解答题 17．各项均为正数的等比数列 的前 项和为 .已知 ， . （Ⅰ）求数列 的通项公式； （Ⅱ）设数列 满足 ，求数列 的前 项和 . 【答案】(1) ;(2) . 【解析】试题分析：(Ⅰ)设 的公比为 ，由 ， ，解得 ，即可求解数列 的通项公式； (Ⅱ)由(Ⅰ)得 ，可得 ，利用等比数列的求和公式，即可求解数 列的前 项和． 试题解析： (Ⅰ)设 的公比为 ，由 ， 得 ， 于是 ，解得 （ 不符合题意，舍去） 故 ． (Ⅱ)由(Ⅰ)得 ，则 ， 则 … ． 18．某组织在某市征集志愿者参加志愿活动，现随机抽出 60 名男生和 40 名女生共 100 人进行调查，统计出 100 名市民中愿意参加志愿活动和不愿意参加志愿活动的男女生比 例情况，具体数据如图所示. (1)完成下列 列联表，并判断是否有 的把握认为愿意参与志愿活动与性别有关？ 愿意 不愿意 总计 男生 女生 总计 (2)现用分层抽样的方法从愿意参加志愿活动的市民中选取 7 名志愿者，再从中抽取 2 人作为队长，求抽取的 2 人至少有一名女生的概率. 参考数据及公式： . 【答案】(1)列联表见解析；没有 99%的把握认为愿意参与志愿活动与性别有关． (2) . 【解析】试题分析：（1）完善 列联表，求出 ，然后判断是否有 的把握认为愿 意参与志愿活动与性别有关； （2）分层抽样的方法从愿意参加志愿活动的市民中选取 7 名志愿者，则女生 4 人，男 生 3 人，分别编号为 从中任取两人的所有基本事件共 有 21 种情况，其中满足两人中至少有一人是女生的基本事件数有 18 个，从而求得抽取 的 2 人至少有一名女生的概率. 试题解析： （Ⅰ） 愿意 不愿意 总计 男生 15 45 60 女生 20 20 40 总计 35 65 100 计算 ， 所以没有 99%的把握认为愿意参与志愿活动与性别有关． （Ⅱ）用分层抽样的方法从愿意参加志愿活动的市民中选取 7 名志愿者，则女生 4 人， 男生 3 人，分别编号为 从中任取两人的所有基本事件 如下： ， ， ，共有 21 种情况，其中满足两人中至少有一人是女生的基本事件数 有 18 个，抽取的 2 人至少有一名女生的概率 ． 点睛：古典概型中基本事件数的探求方法 (1)列举法. (2)树状图法：适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与 “无序”区别的题目，常采用树状图法. (3)列表法：适用于多元素基本事件的求解问题，通过列表把复杂的题目简单化、抽象 的题目具体化. 19．已知正方形 的边长为 2，分别以 ， 为一边在空间中作正三角形 ， ，延长 到点 ，使 ，连接 ， . (1)证明： 平面 ； (2)求点 到平面 的距离. 【答案】（1）见解析；（2）1. 【解析】试题分析：（1）证线面垂直，先证线线垂直，做出辅助线，根据长度关系， 首先证得 ，再证得 ， ，根据线面垂直的判定定理得到 线面垂直；（2）根据条件可得到 平面 ，进而点 到平面 的距离等于 点到平面 的距离，取 的中点为 ，连接 ， 平面 ， 为 点 到平面 的距离. 解析： (1)连接 交 于点 ，并连接 ，则 ，又∵ ， ABCD AB BC PAB PBC CD E 2CE CD= AE PE AE ⊥ PAC B PAE PO BD⊥ PO AE⊥ AE AC⊥ BD  PAE B PAE O PAE AP F OF OF ⊥ PAE OF O PAE BD AC O OP OA OB OC= = PC PA= ∴ ，又∵ ，∴ ，∴ ， ∵ ，∴ 平面 ，∵ 平面 ，∴ ， ∵ ， ，∴ ，∴ ， 即 ，∵ ，∴ 平面 . (2) 由 题 知 ， ， 且 ， 可 得 四 边 形 为 平 行 四 边 形 ， ∴ ， 又∵ 平面 ，∴ 平面 ，∵点 ，∴点 到平面 的距 离等于 点到平面 的距离，取 的中点为 ，连接 ，则由(1)可得 . 在 中 ， ， 则 ， ∴ ，∴ 平面 ，即 为点 到平面 的距离. 在 中， ，得点 到平面 的距离为 1. 20．已知椭圆 的两个焦点分别为 ， ，且椭圆 过点 . (1)求椭圆 的标准方程； (2)若与直线 平行的直线交椭圆 于 ， 两点，当 时，求 的面积. 【答案】(1) (2) 【解析】试题分析：（1）布列方程组求得椭圆 的标准方程；（2）直线 方程为 ， ． 将 直 线 的 方 程 代 入 椭 圆 的 方 程 并 整 理 得 ，利用韦达定理及 可得 ，从而求得 . 试题解析： （Ⅰ）设椭圆 的方程为 ， PO AC⊥ POB POC ≌ 90POB POC∠ = ∠ = ° PO BD⊥ OB OC O∩ = PO ⊥ ABCD AE ⊂ ABCD PO AE⊥ AD CD⊥ AD DE CD= = 45EAD CAD∠ = ∠ = ° 90EAC∠ = ° AE AC⊥ PO AC O∩ = AE ⊥ PAC AB DE AB DE= ABDE BD AE BD ⊄ PAE BD  PAE O BD∈ B PAE O PAE AP F OF OF AE⊥ Rt ABC ( )22 2 22 2 2PO PB BO= − = − = PO AO= OF PA⊥ OF ⊥ PAE OF O PAE Rt POA 1 12OF PA= = B PAE 由题意可得 解得 故椭圆 的方程为 ． （Ⅱ）直线 的方程为 ， 设直线 方程为 ， ． 将直线 的方程代入椭圆 的方程并整理得 ， 由 ，得 ， ， 由 得， ， ， ， ， ， 得 ． 又 ， 到直线 的距离 ． 所以 ． 21．已知函数 ， ，其中 是自然常数. (1)判断函数 在 内零点的个数，并说明理由； (2) ， ，使得不等式 成立，试求实数 的取值范围. 【答案】(1) 存在 1 个零点；理由见解析. (2) . 【解析】分析：（1） 在 内零点的个数 1，求得 的导数，判断符号，可得 单调性，再由函数零点存在定理，即可得到结论； （2）由题意可得 ，即 ，分别求 得 在 上的单调性，可得最值，解 的不等式，即可得到所求范围． 详解： (1)函数 在 上的零点的个数为 1，理由如下： 因为 ，所以 ， 因为 ，所以 ，所以函数 在 上单调递增. 因为 ， ， 根据函数零点存在性定理得函数 在 上存在 1 个零点. (2)因为不等式 等价于 ， 所以 ， ，使得不等式 成立，等价于 ，即 ， 当 时， ，故 在区间 上单调递增， 所以当 时， 取得最小值 ，又 ， 当 时， ， ， ，所以 ， 故函数 在区间 上单调递减. 因此，当 时， 取得最大值 ，所以 ，所以 ， 所以实数 的取值范围为 . 点睛：本题考查导数的运用：求单调性和最值，考查函数零点存在定理的运用，存在性 和任意性问题解法，考查转化思想和运算化简能力，属于中档题． 22．选修 4-4：坐标系与参数方程 在 直 角 坐 标 系 中 ， 曲 线 的 参 数 方 程 为 （ 其 中 为 参 数 ），曲 线 ，以坐标原点 为极点，以 轴正半轴为极轴建立极坐标系. (Ⅰ)求曲线 的普通方程和曲线 的极坐标方程； (Ⅱ)若射线 与曲线 ， 分别交于 两点，求 . 【答案】(1) ； . (2) . 【解析】试题分析：（1）由 sin 2α+cos2α=1，能求出曲线 C1 的普通方程，由 x=ρcosθ，y=ρsinθ，能求出曲线 C2 的极坐标方程；（2）依题意设 A（ ）， B（ ），将 代入曲线 C1 的极坐标方程，求出 ρ1=3，将 （ρ＞ 0）代入曲线 C2 的极坐标方程求出 ，由此能求出|AB|． 解析： （Ⅰ）由 得 . 所以曲线 的普通方程为 . 把 ，代入 ，得到 ，化简得到曲线 的极坐标方程为 . （Ⅱ）依题意可设 ,曲线 的极坐标方程为 . 将 代入 的极坐标方程得 ，解得 . 将 代入 的极坐标方程得 . 所以 . 23．[选修 4-5：不等式选讲] 设函数 ，其中 . (Ⅰ)当 时，求不等式 的解集； (Ⅱ)若 时，恒有 ，求 的取值范围. 【答案】(1) . (2) . 【解析】试题分析：（1）当 时， ，化为 ，可得 或 ，从而可得不等式 的解集；（2）化简 ，因为 ，∴ 时， 恒成立，又 时，当 时， ，∴只需 即可， 所以 . 试题解析：（1）当 时， ， 所以 ，所以 或 ， 解集为 . （2） ，因为 ，∴ 时， 恒成立， 又 时，当 时， ，∴只需 即可， 所以 .