2020年浙江新高考数学二轮复习教师用书：专题五　4 高考解答题的审题与答题示范（五） 2页

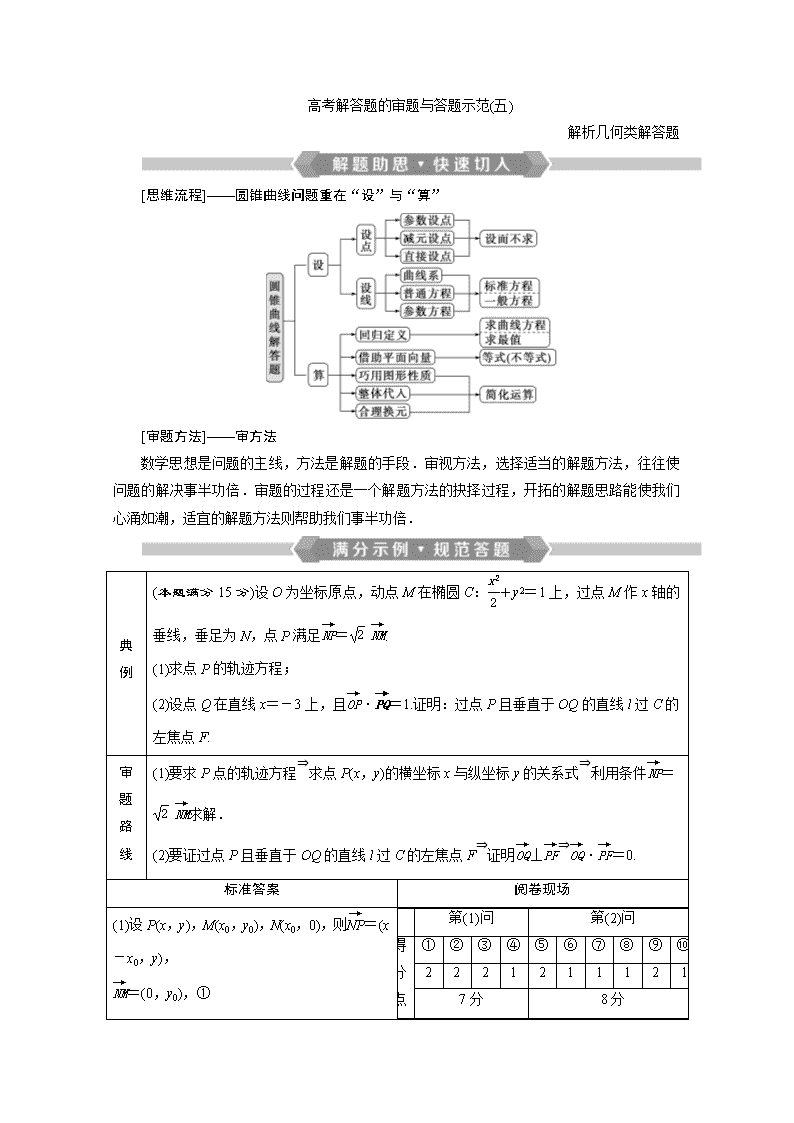
高考解答题的审题与答题示范(五)‎ 解析几何类解答题 ‎[思维流程]——圆锥曲线问题重在“设”与“算”‎ ‎[审题方法]——审方法 数学思想是问题的主线，方法是解题的手段．审视方法，选择适当的解题方法，往往使问题的解决事半功倍．审题的过程还是一个解题方法的抉择过程，开拓的解题思路能使我们心涌如潮，适宜的解题方法则帮助我们事半功倍．‎ 典例 ‎(本题满分15分)设O为坐标原点，动点M在椭圆C：＋y2＝1上，过点M作x轴的垂线，垂足为N，点P满足＝ .‎ ‎(1)求点P的轨迹方程；‎ ‎(2)设点Q在直线x＝－3上，且·＝1.证明：过点P且垂直于OQ的直线l过C的左焦点F.‎ 审题路线 ‎(1)要求P点的轨迹方程⇒求点P(x，y)的横坐标x与纵坐标y的关系式⇒利用条件＝ 求解．‎ ‎(2)要证过点P且垂直于OQ的直线l过C的左焦点F⇒证明⊥⇒·＝0.‎ 标准答案 阅卷现场 ‎(1)设P(x，y)，M(x0，y0)，N(x0，0)，则＝(x－x0，y)，‎ ＝(0，y0)，①‎ 第(1)问 第(2)问 得 分 点 ‎①‎ ‎②‎ ‎③‎ ‎④‎ ‎⑤‎ ‎⑥‎ ‎⑦‎ ‎⑧‎ ‎⑨‎ ‎⑩‎ ‎2‎ ‎2‎ ‎2‎ ‎1‎ ‎2‎ ‎1‎ ‎1‎ ‎1‎ ‎2‎ ‎1‎ ‎7分 ‎8分 由＝ ，‎ 得x0＝x，y0＝y，②‎ 因为M(x0，y0)在C上，‎ 所以＋＝1，③‎ 因此点P的轨迹方程为x2＋y2＝2.④‎ ‎(2)证明：由题意知F(－1，0)，‎ 设Q(－3，t)，P(m，n) ，‎ 设而不求 则＝(－3，t)，＝(－1－m，－n)，⑤‎ ·＝3＋3m－tn，⑥‎ ＝(m，n)，＝(－3－m，t－n)，⑦‎ 由·＝1得－3m－m2＋tn－n2＝1，⑧‎ 又由(1)知m2＋n2＝2，故3＋3m－tn＝0.‎ 所以·＝0，即⊥，⑨‎ 又过点P存在唯一直线垂直于OQ，所以过点P且垂直于OQ的直线l过C的左焦点F.⑩‎ 第(1)问踩点得分说明 ‎①设出点P、M、N的坐标，并求出和的坐标得2分；‎ ‎②由＝ ，正确求出x0＝x，y0＝y得2分；‎ ‎③代入法求出＋＝1得2分；‎ ‎④化简成x2＋y2＝2得1分．‎ 第(2)问踩点得分说明 ‎⑤求出和的坐标得2分；‎ ‎⑥正确求出·的值得1分；‎ ‎⑦正确求出和的坐标得1分；‎ ‎⑧由·＝1得出－3m－m2＋tn－n2＝1得1分；‎ ‎⑨得出⊥得2分；‎ ‎⑩写出结论得1分.‎