数学文卷·2018届河南省信阳市普通高中高三第二次教学质量检测（2018 7页

信阳市2017—2018学年普通高中高三第二次教学质量检测 数 学（文科）‎ ‎ 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。考生作答时，将答案答在答题卡上，在本试卷上答题无效。考试结束后，将本试卷和答题卡一并交回。‎ 注意事项：‎ ‎ 1．答题前，考生在答题卡上务必用直径0．5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，并帖好条形码。请认真核准条形码的准考证号、姓名和科目。‎ ‎ 2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，在试题卷上作答无效。 ‎ 第Ⅰ卷 （满分60分）‎ 一、选择题：本大题共12小题，每小题5分，满分60分。在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．复数z＝的实部与虚部分别为 ‎ A．7，－3 B．7，－3i C．－7，3 D．－7，3i ‎2．已知全集U＝R，集合A＝{x｜x＜－，或x＞1}，B＝{x｜－1≤x≤2，x∈Z}，则图1 ‎ 所示的阴影部分表示的集合等于 ‎ A．{－1，2} B．{－1，0}‎ ‎ C．{1，2} D．{0，1}‎ ‎3．已知命题p：∈R，－x－1≤0，则为 ‎ A．R，－x－1＞0 B．∈R，－x－1≥0‎ ‎ C．∈R，－x－1＞0 D．∈R，－x－1＞0‎ ‎4．已知双曲线（a＞0，b＞0）的一条渐近线经过点（3，），则双曲线的离心率为 ‎ A． B．2 C．或2 D．或2‎ ‎5．某同学先后投掷一枚骰子两次，第一次向上的点数记为x，第二次向上的点数记为y．在直角坐标系xOy中，以（x，y）为坐标的点落在直线2x－y＝1上的概率为 ‎ A． B． C． D．‎ ‎6．如果f（x）是定义在R上的奇函数，那么下列函数中，一定为偶函数的是 ‎ A．y＝x＋f（x） B．y＝＋f（x） C．y＝xf（x） D．y＝f（x）‎ ‎7．已知等比数列{}的前n项和为，a1＋a3＝，且a2＋a4＝，则等于 ‎ A．－1 B． C． D．‎ ‎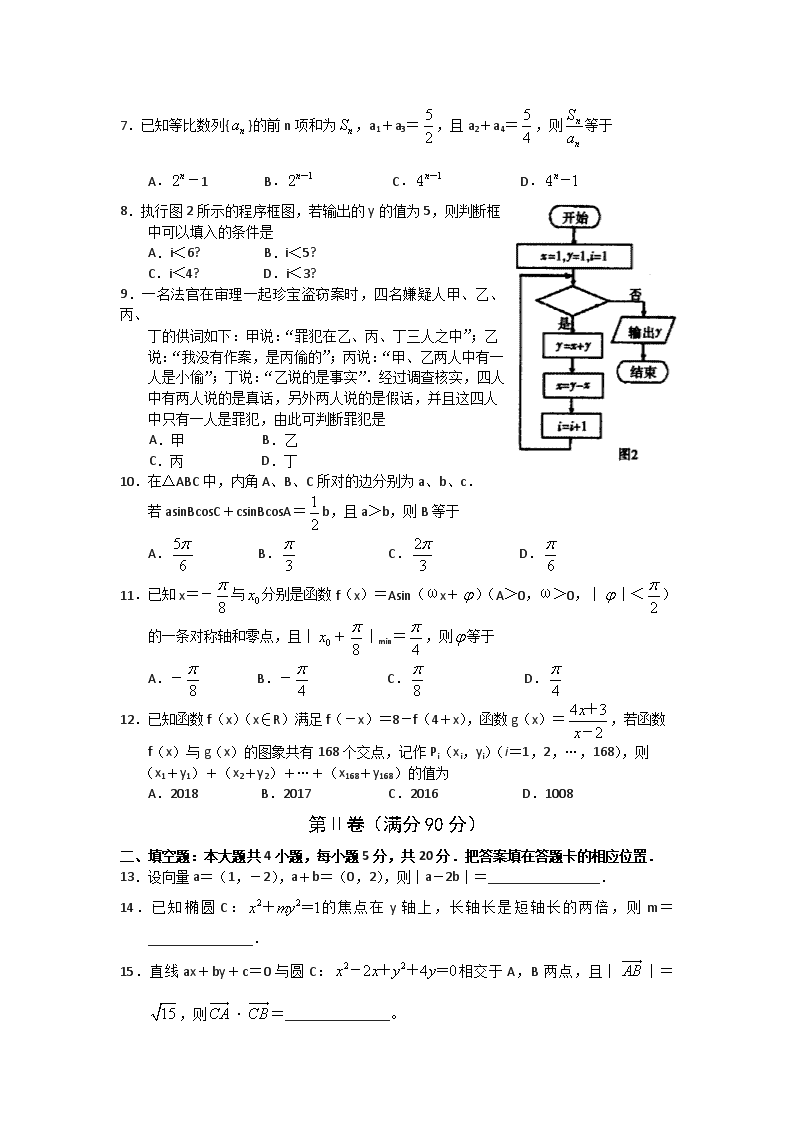8．执行图2所示的程序框图，若输出的y的值为5，则判断框 中可以填入的条件是 ‎ A．i＜6? B．i＜5? ‎ ‎ C．i＜4? D．i＜3?‎ ‎9．一名法官在审理一起珍宝盗窃案时，四名嫌疑人甲、乙、丙、‎ 丁的供词如下：甲说：“罪犯在乙、丙、丁三人之中”；乙 说：“我没有作案，是丙偷的”；丙说：“甲、乙两人中有一 人是小偷”；丁说：“乙说的是事实”．经过调查核实，四人 中有两人说的是真话，另外两人说的是假话，并且这四人 中只有一人是罪犯，由此可判断罪犯是 A．甲 B．乙 ‎ C．丙 D．丁 ‎10．在△ABC中，内角A、B、C所对的边分别为a、b、c．‎ 若asinBcosC＋csinBcosA＝b，且a＞b，则B等于 ‎ A． B． C． D．‎ ‎11．已知x＝－与分别是函数f（x）＝Asin（ωx＋）（A＞0，ω＞0，｜｜＜）的一条对称轴和零点，且｜＋｜min＝，则等于 ‎ A．－ B．－ C． D．‎ ‎12．已知函数f（x）（x∈R）满足f（－x）＝8－f（4＋x），函数g（x）＝，若函数 f（x）与g（x）的图象共有168个交点，记作Pi（xi，yi）（i＝1，2，…，168），则 ‎（x1＋y1）＋（x2＋y2）＋…＋（x168＋y168）的值为 ‎ A．2018 B．2017 C．2016 D．1008‎ 第Ⅱ卷（满分90分）‎ 二、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡的相应位置． ‎ ‎13．设向量a＝（1，－2），a＋b＝（0，2），则｜a－2b｜＝________________．‎ ‎14．已知椭圆C：的焦点在y轴上，长轴长是短轴长的两倍，则m＝_______________．‎ ‎15．直线ax＋by＋c＝0与圆C：相交于A，B两点，且｜｜＝‎ ‎，则·＝_______________。‎ ‎16．某化肥厂生产甲、乙两种肥料，生产一车皮甲肥料需要磷酸盐4吨、硝酸盐18吨；生产一车皮乙种肥料需要磷酸盐1吨、硝酸盐15吨．已知生产一车皮甲种肥料产生的利润是10万元，生产一车皮乙种肥料产生的利润是5万元．现库存磷酸盐10吨、硝酸盐66吨，如果该厂合理安排生产计划，则可以获得的最大利润是____________万元．‎ 三、解答题：本大题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。第17～21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎17．（本小题满分12分）‎ ‎ 已知△ABC的内角A，B，C的对边分别为a，b，c，且acosB＋bsinA＝0． ‎ ‎ （Ⅰ）求角B的大小；‎ ‎ （Ⅱ）若a＋c＝4，b＝，求△ABC的面积．‎ ‎18．（本小题满分12分）‎ 已知等差数列{}的前n和为，且S5＝45，S6＝60．‎ ‎（Ⅰ）求数列{}的通项公式；‎ ‎（Ⅱ）若数列{}满足－＝（n∈N﹡），且b1＝3，求数列{}的前n和为．‎ ‎19．（本小题满分12分）‎ ‎ 二手车经销商小王对其所经营的某一型号二手汽车的使用年数x（0＜x≤10）与销售价格y （单位：万元／辆）进行整理，得到如表的对应数据：‎ 使用年数 ‎2‎ ‎4‎ ‎6‎ ‎8‎ ‎10‎ 售价 ‎16‎ ‎13‎ ‎9.5‎ ‎7‎ ‎4.5‎ ‎ （Ⅰ）试求y关于x的回归直线方程；‎ ‎ （Ⅱ）已知每辆该型号汽车的收购价格为ω＝0．05－1．75x＋17．2（单位：万元），根据（Ⅰ）中所求的回归方程，预测x为何值时，小王销售一辆该型号汽车所获得的利润z（单位：万元）最大?‎ ‎20．（本小题满分12分）‎ ‎ 已知抛物线C：＝2py（p＞0）的焦点为F，过点F的直线l 交C于A，B两点，且以AB为直径的圆M与直线y＝－1相切于点N．‎ ‎ （Ⅰ）求抛物线C的方程；‎ ‎ （Ⅱ）若圆M与直线x＝－相切于点Q，求直线l的方程和圆M的方程．‎ ‎21．（本小题满分12分）‎ 已知函数f（x）＝＋－a，g（x）＝f（x）＋b，其中a，b为常数．‎ ‎（Ⅰ）若x＝1是函数y＝xf（x）的一个极值点，求曲线y＝f（x）在点（1，f（1））处的切线方程；‎ ‎（Ⅱ）若函数f（x）有2个零点，f（g（x））有6个零点，求a＋b的取值范围．‎ ‎ ‎ 选考题：共10分。请考生从第22、23题中任选一题作答，并用2B铅笔将答题卡上所选题目对应的题号右侧方框涂黑，按所涂题号进行评分；多涂、多答，按所涂的首题进行评分；不涂，按本选考题的首题进行评分。‎ ‎22．（本小题满分10分）选修4—4：坐标系与参数方程 已知直线l的参数方程为（其中t为参数），曲线C1：＋－3＝0，以坐标原点为极点，x轴正半轴为极轴，建立极坐标系，两种坐标系中取相同长度单位．‎ ‎ （Ⅰ）求直线l的普通方程及曲线C1的直角坐标方程；‎ ‎ （Ⅱ）在曲线C1上是否存在一点P，使点P到直线l的距离最大?若存在，求出距离的最大值及点P的直角坐标；若不存在，请说明理由．‎ ‎23．（本小题满分10分）选修4—5：不等式选讲 已知函数f（x）＝｜x－5｜—｜x－2｜．‎ ‎（Ⅰ）若∈R，使得f（x）≤m成立，求实数m的取值范围；‎ ‎（Ⅱ）解不等式－8x＋15＋f（x）≤0．‎