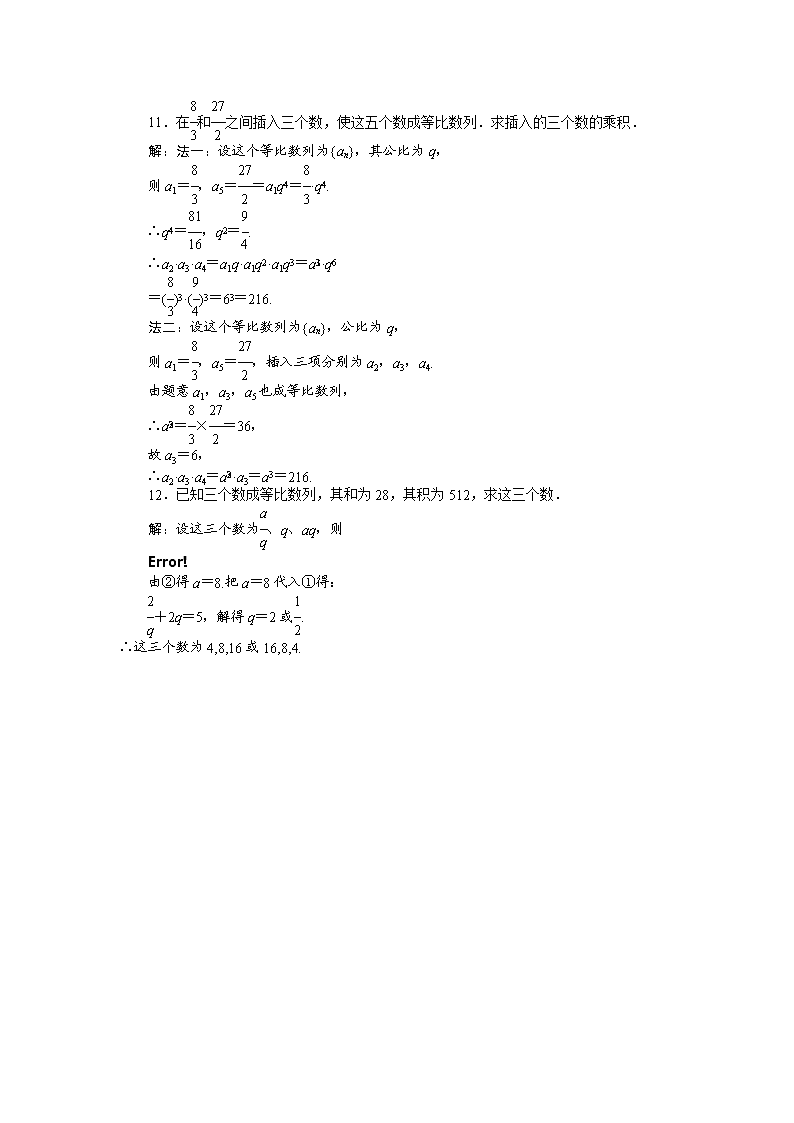高中数学必修5第2章2_4_2同步训练及解析 3页

人教A高中数学必修5同步训练 ‎1．在等比数列{an}中，a1＝5，a‎9a10＝100，则a18＝(　　)‎ A．18　　　　　　　　　　 B．19‎ C．20 D．21‎ 答案：C ‎2．在等比数列{an}中，a1＝1，公比|q|≠1.若am＝a‎1a2a3a4a5，则m＝(　　)‎ A．9 B．10‎ C．11 D．12‎ 解析：选C.在等比数列{an}中，‎ ‎∵a1＝1，∴am＝a‎1a2a3a4a5＝aq10＝q10.‎ 又∵am＝qm－1，∴m－1＝10，∴m＝11.‎ ‎3．各项均为实数的等比数列{an}中，a2＝1，a4＝9，则a3＝________.‎ 答案：±3‎ ‎4．已知等比数列{an}中，a‎2a6a10＝1，求a‎3a9.‎ 解：法一：∵a‎2a10＝a，∴a‎2a6a10＝a＝1.‎ ‎∴a6＝1.∴a‎3a9＝a＝1.‎ 法二：设公比为q，‎ 则a‎2a6a10＝a1q·a1q5·a1q9＝aq15＝1，‎ ‎∴a1q5＝1.‎ ‎∴a‎3a9＝a1q2·a1q8＝(a1q5)2＝1.‎ 一、选择题 ‎1．已知{an}是等比数列，a6＝2，a3＝，则公比q等于(　　)‎ A．－ B．－2‎ C．2 D. 解析：选C.∵{an}是等比数列，∴＝q3＝8.∴q＝2.‎ ‎2．已知等比数列{an}中，a3＝－4，a6＝54，则a9等于(　　)‎ A．54 B．－81‎ C．－729 D．729‎ 解析：选C.∵a3·a9＝a，∴－‎4a9＝542，∴a9＝－729.‎ ‎3．将公比为q的等比数列{an}依次取相邻两项的乘积组成新的数列a‎1a2，a‎2a3，a‎3a4，….则此数列(　　)‎ A．是公比为q的等比数列 B．是公比为q2的等比数列 C．是公比为q3的等比数列 D．不一定是等比数列 解析：选B.设新数列为{bn}，则{bn}的通项公式为bn＝anan＋1.所以＝＝q2，数列{bn}是公比为q2的等比数列．‎ ‎4．在等比数列{an}中，an＞0，若a‎1a2a3…a2012＝22012，则a‎2a2011＝(　　)‎ A．2 B．4‎ C．21005 D．21006‎ 解析：选B.a‎1a2a3…a2012＝22012，∴(a‎1a2012)1006＝22012＝41006，∴a‎1a2012＝4，∴a‎2a2011＝4.‎ ‎5．在等比数列{an}中，a‎3a4a5＝3，a‎6a7a8＝24，则a‎9a10a11＝(　　)‎ A．48 B．72‎ C．144 D．192‎ 解析：选D.∵＝q9＝8(q为公比)，‎ ‎∴a‎9a10a11＝a‎6a7a8·q9＝24×8＝192.‎ ‎6．在等比数列{an}中，首项a1<0，要使数列{an}对任意正整数n都有an＋1>an，则公比q应满足(　　)‎ A．q>1 B．00对任意正整数n都成立，而a1<0，只能00，若a‎1a5＝16，a4＝8，则a5＝________.‎ 解析：∵an>0，a‎1a5＝16，∴a3＝4.‎ 又∵a＝a‎3a5，∴a5＝16.‎ 答案：16‎ ‎9．在等比数列{an}中，a‎7a11＝6，a4＋a14＝5，则＝________.‎ 解析：因为a‎7a11＝a‎4a14＝6，又a4＋a14＝5，所以或.所以＝q10＝，所以＝或＝.‎ 答案：或 三、解答题 ‎10．已知数列{an}为等比数列．‎ ‎(1)若a1＋a2＋a3＝21，a‎1a2a3＝216，求an；‎ ‎(2)若a‎3a5＝18，a‎4a8＝72，求公比q.‎ 解：(1)∵a‎1a2a3＝a＝216，∴a2＝6，‎ ‎∴a‎1a3＝36且a1＋a3＝21－a2＝15.‎ ‎∴a1，a3是方程x2－15x＋36＝0的两根3和12.‎ 当a1＝3时，q＝＝2，an＝3·2n－1；‎ 当a1＝12时，q＝，an＝12·()n－1＝3·23－n.‎ ‎(2)∵a‎4a8＝a3q·a5q3＝a‎3a5q4＝18q4＝72，‎ ‎∴q4＝4，∴q＝±.‎ ‎11．在和之间插入三个数，使这五个数成等比数列．求插入的三个数的乘积．‎ 解：法一：设这个等比数列为{an}，其公比为q，‎ 则a1＝，a5＝＝a1q4＝·q4.‎ ‎∴q4＝，q2＝.‎ ‎∴a2·a3·a4＝a1q·a1q2·a1q3＝a·q6‎ ‎＝()3·()3＝63＝216.‎ 法二：设这个等比数列为{an}，公比为q，‎ 则a1＝，a5＝，插入三项分别为a2，a3，a4.‎ 由题意a1，a3，a5也成等比数列，‎ ‎∴a＝×＝36，‎ 故a3＝6，‎ ‎∴a2·a3·a4＝a·a3＝a＝216.‎ ‎12．已知三个数成等比数列，其和为28，其积为512，求这三个数．‎ 解：设这三个数为、q、aq，则 由②得a＝8.把a＝8代入①得：‎ ＋2q＝5，解得q＝2或.‎ ‎∴这三个数为4,8,16或16,8,4. ‎