河北省衡水中学2018届高三上学期一调考试数学（理）试题+Word版 9页

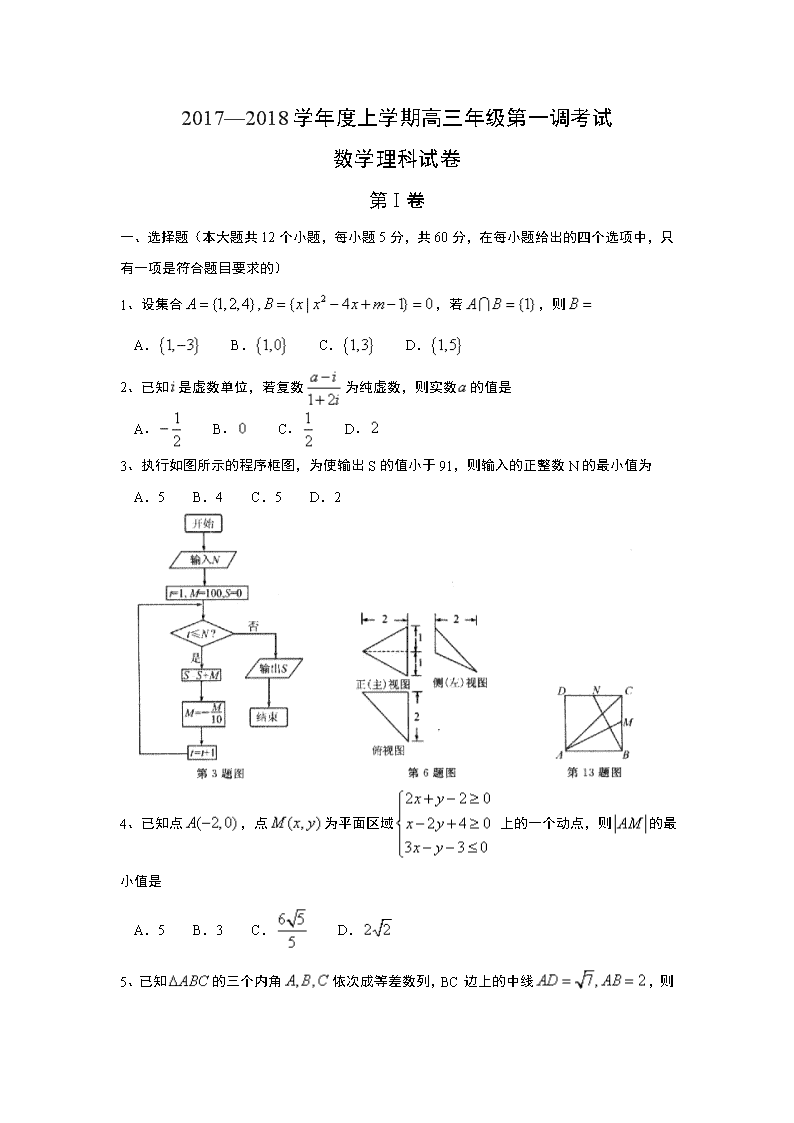
2017—2018 学年度上学期高三年级第一调考试 数学理科试卷 第Ⅰ卷 一、选择题（本大题共 12 个小题，每小题 5 分，共 60 分，在每小题给出的四个选项中，只 有一项是符合题目要求的） 1、设集合 ，若 ，则 A． B． C． D． 2、已知 是虚数单位，若复数 为纯虚数，则实数 的值是 A． B． C． D． 3、执行如图所示的程序框图，为使输出 S 的值小于 91，则输入的正整数 N 的最小值为 A．5 B．4 C．5 D．2 4、已知点 ，点 为平面区域 上的一个动点，则 的最 小值是 A．5 B．3 C． D． 5、已知 的三个内角 依次成等差数列，BC 边上的中线 ，则 2{1,2,4}, { | 4 1} 0A B x x x m= = − + − = {1}A B = B = { }1, 3− { }1,0 { }1,3 { }1,5 i 1 2 a i i − + a 1 2 − 0 1 2 2 ( 2,0)A − ( , )M x y 2 2 0 2 4 0 3 3 0 x y x y x y + − ≥  − + ≥  − − ≤ AM 6 5 5 2 2 ABC∆ , ,A B C 7, 2AD AB= = A．3 B． C． D． 6、一个几何体的三视图如图所示，则该几何体的所有棱中，最长的棱长为 A．3 B． C． D． 7、已知数列 满足 ，则 A．0 B． C． D． 8、已知 ，函数 在 内单调递减，则 的取值范围是 A． B． C． D． 9、设函数 ，其中 ，若 ， 且 的最小正周期大于 ，则 A ． B ． C ． D． 10、已知函数 ，若实数 满足 ，则实数 的取值范围是 A． B． C． D． 11、已知函数 的图象的一对称中心的横坐标为 ，且 有 三个零点，则实数 的取值范围是 A． B． C． D． 12、定义在内的函数满足：①当 时， ；② （ 为正常数），若函数的所有极大值点都在同一直线上，则常数 的值是 A．1 B． C． 或 3 D．1 或 2 ABCS∆ = 2 3 3 3 6 2 3 2 2 5 { }na 1 1 31, 3 1 n n n aa a a+ −= = + 20a = 3− 3 3 2 0w > ( ) sin( )3f x wx π= − ( , )3 2 π π w 11(0, ]3 5 11[ , ]2 3 1(0, ]2 1 3[ , ]2 4 ( ) 2sin( ),f x wx x Rϕ= + ∈ 0,w ϕ π> < 5 11( ) 2, ( ) 08 8f f π π= = ( )f x 2π 1 7,3 24w πϕ= = 2 11,3 12w πϕ= = − 1 7,3 24w πϕ= = − 2 ,3 12w πϕ= = − ( ) 31( )x xf x e xe = − a ( )2 0.5(log ) (log ) 2 1f a f a f+ ≤ a 1( , ) (2, )2 −∞ +∞ 1( , ] [2, )2 −∞ +∞ 1[ ,2]2 1( ,2)2 ( ) 3 2 1f x x ax= + + 0 0( 0)x x > ( )f x a ( ,0)−∞ 3 2( , )2 −∞ − (0, )+∞ ( , 1)−∞ − 2 4x≤ ≤ ( ) 1 3f x x= − − ( ) ( )2f x cf x= c c 2± 1 2 第Ⅱ卷 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分，把答案填在答题卷的横线上。. 13、如图，正方形 ABCD 中，M、N 分别是 BC、CD 的中点，若 ，则 14、已知定义在实数集 R 上的函数 满足 ，且 的导函数 ， 则不等式 的解集为 15、已知数列 的前 n 项和 ，且成等比数列， 成等差数列，则 等于 16 、 已 知 函 数 是 定 义 域 为 R 的 偶 函 数 ， 当 时 ， 若关于 的方程 有且仅有 6 个不同的实数根，则实数 的取值范围是 三、解答题：本大题共 6 小题，满分 70 分，解答应写出文字说明、证明过程或演算步骤 （一）必考题：共 60 分 17、（本小题满分 10 分） 在 中，角 的对边分别是 ，且 。 （1）求角 A 的大小； （2）求 的取值范围。 18、（本小题满分 12 分） 高三某班 12 月月考语文成绩服从正态分布 ，数学成绩的频率分布直方图如 图，如果成绩大于 135 分，则认为特别优秀。 （1）这 500 名学生中本次考试语文、数学特别优秀的大约各多少人？ （2）如果语文和数学两科都特别优秀的共有 6 人，从（1）中的这些同学随机抽取 3 人， AC AM BNλ µ= +   λ µ+ = ( )f x ( )1 4f = ( )f x ( ) 3f x′ < (ln ) 3ln 1f x x> + { }na 1 2, 6, 4, 0n nS S S S= = > 2 1 2 2 2 1, ,n n nS S S− + − 2016a ( )y f x= 0x ≥ ( ) 5 sin( ),0 14 2 1( ) 1, 14 x x x f x x π ≤ ≤=   + > x ( )25[ ( )] (5 6) 6 0( )f x a f x a a R− + + = ∈ a ABC∆ , ,A B C , ,a b c 3 cos (2 3 )cosa C b c A= − 25cos( ) 2sin2 2 CB π − − 2(100,17.5 )N 设三人中两科都特别优秀的有 X 人，求 X 的分布列和数学期望。 参 考 数 据 ： 若 ， 则 。 19、（本小题满分 12 分） 如图①，在平行四边形 中， 分别为 的中点，现把平行四边形 沿折起，如图②所示，连接 。 （1）求证： ； （2）若 ，求二面角 的余弦值。 20、（本小题满分 12 分） 已知曲线 在点 处的切线是 。 （1）求实数 的值； （2）若 对任意 恒成立，求实数 的最大值。 21、（本小题满分 12 分） 2( , )X N µ σ ( ) 0.68, ( 2 2 ) 0.96P X P Xµ σ µ σ µ σ µ σ− < < + = − < < + = 1 1ABB A 0 1 1 160 , 4, 2, ,ABB AB AA C C∠ = = = 1,AB A B 1 1AAC C 1 1 1 1, ,B C B A B A 1 1AB CC⊥ 1 6AB = 1 1C AB A− − ( ) 2 lnf x ax bx x= + (1, (1))f 2 1y x= − ,a b ( ) 2 ( 1)f x kx k x≥ + − (0, )x∈ +∞ k 已知函数 为常数， ） （1）当 时，求函数 在 处的切线方程； （2）当 在 处取得极值时，若关于 的方程 在 上恰有两 个不同的相等的实数根，求实数 的取值范围； （3）若对任意的 ，总存在 ，使不等式 成立， 求实数 的取值范围。 请考生在第（22）、（23）题中任选一题作答，如果多做，则按所做的第一题记分，作答时用 2B 铅笔在答题卡上把所选题目的题号涂黑，把答案填在答题卡上． 22、（本小题满分 10 分） 选修 4-4 坐标系与参数方程 已知极坐标系的极点在直角坐标系的原点处，极轴与 x 轴非负半轴重合，直线 的参数方 程为 为参数），曲线 C 的极坐标方程为 。 （1）写出曲线 C 的直角坐标方程和直线 的普通方程； （2）设直线 与曲线 C 相交于 两点，求 的值。 23、（本小题满分 10 分））选修 4-5 不等式选讲 已知函数 。 （1）解不等式 ； （2）若对于任意 ，都有 ，使得成立，求实数 的取值范围。 ( ) 21 1ln( ) (2 2f x ax x ax a= + − − 0a > 1a = ( )f x 1x = ( )y f x= 1 2x = x ( ) 0f x b− = [0,2] b (1,2)a∈ 1[ ,1]2x∈ 2 0( ) ( 2 3)f x m a a> + − m l 31 2 ( 1 2 x t t y t  = − +  = 4cosρ θ= l l ,P Q PQ ( ) ( )2 2 3 , 1 2f x x a x g x x= − − + = − + ( ) 5g x < x R∈ ( ) ( )1 2f x g x= a