专题14 空间向量与立体几何（仿真押题）-2017年高考数学（理）命题猜想与仿真押题 24页

专题14 空间向量与立体几何（仿真押题）‎ ‎2017年高考数学（理）命题猜想与仿真押题 ‎1．有以下命题：‎ ‎①如果向量a，b与任何向量不能构成空间向量的一个基底，那么a，b的关系是不共线；‎ ‎②O，A，B，C为空间四点，且向量，，不构成空间的一个基底，那么点O，A，B，C一定共面；‎ ‎③已知向量a，b，c是空间的一个基底，则向量a＋b，a－b，c也是空间的一个基底．‎ 其中正确的命题是(　　)‎ A．①② B．①③ C．②③ D．①②③‎ ‎2．已知a＝(2，－1，3)，b＝(－1，4，－2)，c＝(7，5，λ)，若a，b，c三向量共面，则实数λ等于(　　)‎ A. B. C. D. 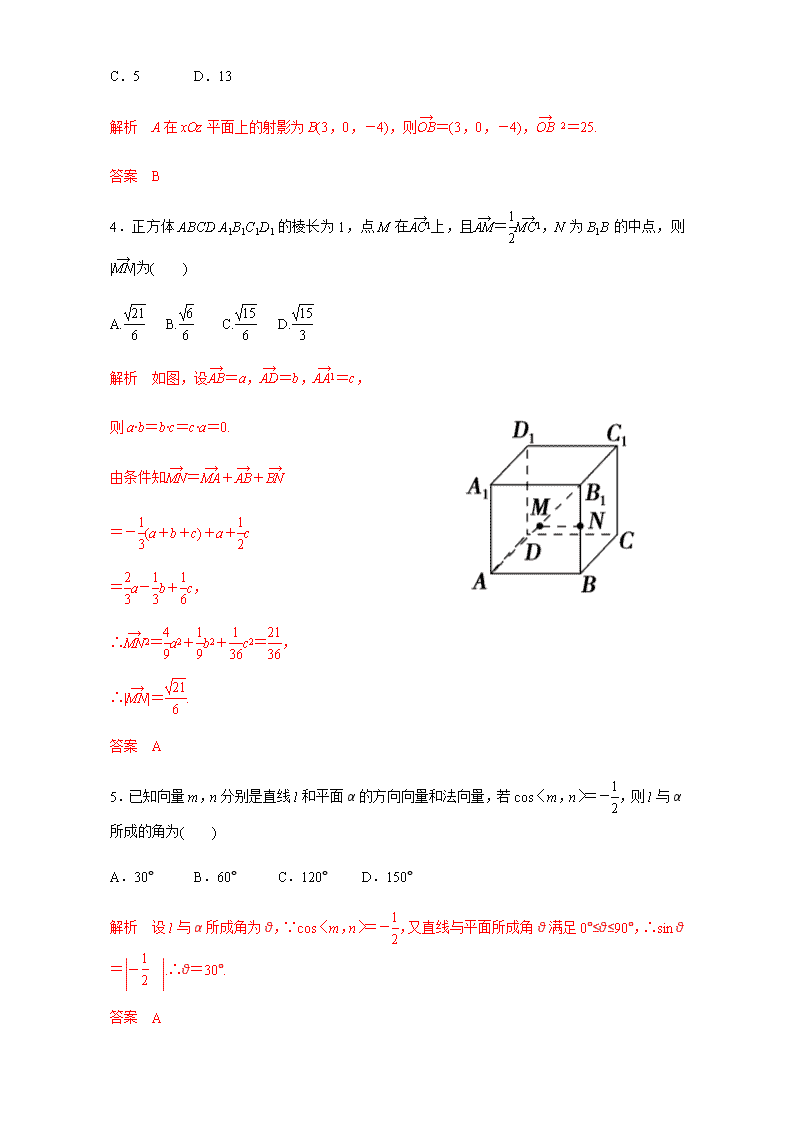解析　由题意得c＝ta＋μb＝(2t－μ，－t＋4μ，3t－2μ)，‎ ‎∴解得 答案　D ‎3．已知点B是点A(3，7，－4)在xOz平面上的射影，则2等于(　　)‎ A．(9，0，16) B．25 ‎ C．5 D．13‎ 解析　A在xOz平面上的射影为B(3，0，－4)，则＝(3，0，－4)， 2＝25.‎ 答案　B ‎4．正方体ABCDA1B1C1D1的棱长为1，点M在上，且＝，N为B1B的中点，则||为(　　)‎ A. B. C. D. 解析　如图，设＝a，＝b，＝c，‎ 则a·b＝b·c＝c·a＝0.‎ 由条件知＝＋＋ ‎＝－(a＋b＋c)＋a＋c ‎＝a－b＋c，‎ ‎∴2＝a2＋b2＋c2＝，‎ ‎∴||＝.‎ 答案　A ‎5．已知向量m，n分别是直线l和平面α的方向向量和法向量，若cos〈m，n〉＝－，则l与α所成的角为(　　)‎ A．30° B．60° C．120° D．150°‎ 解析　设l与α所成角为θ，∵cos〈m，n〉＝－，又直线与平面所成角θ满足0°≤θ≤90°，∴sin θ＝.∴θ＝30°.‎ 答案　A ‎6．在正方体ABCD－A1B1C1D1中，M，N分别为棱AA1和BB1的中点，则sin〈，〉的值为(　　)‎ A. B. C. D. 答案　B ‎7．设正方体ABCDA1B1C1D1的棱长为2，则点D1到平面A1BD的距离是(　　)‎ A. B. C. D. 解析　如图，建立空间直角坐标系，则D1(0，0，2)，A1(2，0，2)，D(0，0，0)，B(2，2，0)，‎ ‎∴＝(2，0，0)，＝(2，0，2)，＝(2，2，0)，‎ 设平面A1BD的法向量n＝(x，y，z)，‎ 则令x＝1，则n＝(1，－1，－1)．‎ ‎∴点D1到平面A1BD的距离 d＝＝＝.‎ 答案　D ‎8．二面角αlβ等于120°，A、B是棱l上两点，AC、BD分别在半平面α、β内，AC⊥l，BD⊥l，且AB＝AC＝BD＝1，则CD的长等于(　　)‎ A. B. C．2 D. ‎9.如图所示，已知空间四边形OABC，OB＝OC，且∠AOB＝∠AOC＝，则cos〈，〉的值为(　　)‎ A．0　　　 B.　　　 C.　　　 D. 解析　设＝a，＝b，＝c，由已知条件〈a，b〉＝〈a，c〉＝，且|b|＝|c|，‎ ·＝a·(c－b)＝a·c－a·b ‎＝|a||c|－|a||b|＝0，‎ ‎∴cos〈，〉＝0.‎ 答案　A ‎10．若两点的坐标是A(3cos α，3sin α，1)，B(2cos β，2sin β，1)，则|AB|的取值范围是(　　)‎ A．0，5] B．1，5] ‎ C．(0，5) D．1，25]‎ ‎11．已知空间三点A(0，2，3)，B(－2，1，6)，C(1，－1，5)．则以，为边的平行四边形的面积为________．‎ 解析　由题意可得：‎ ＝(－2，－1，3)，＝(1，－3，2)，‎ ‎∴cos〈，〉＝ ‎＝＝＝.∴sin〈，〉＝.‎ ‎∴以，为边的平行四边形的面积 S＝2×||·||·sin〈，〉＝14×＝7.‎ 答案　7 ‎12．将锐角A为60°，边长为a的菱形ABCD沿BD折成60°的二面角，则A与C之间的距离为________．‎ 解析　设折叠后点A到达A1点的位置，取BD的中点E，连接A1E、CE.‎ ‎∴BD⊥CE，BD⊥A1E. ‎ ‎∴∠A1EC为二面角A1BDC的平面角．‎ ‎∴∠A1EC＝60°，又A1E＝CE，‎ ‎∴△A1EC是等边三角形．‎ ‎∴A1E＝CE＝A1C＝a.‎ 即折叠后点A与C之间的距离为a.‎ 答案　a ‎13.如图，△ABC是以∠ABC为直角的三角形，SA⊥平面ABC，SA＝BC＝2，AB＝4.M，N，D分别是SC，AB，BC的中点．‎ ‎(1)求证：MN⊥AB；‎ ‎(2)求二面角SNDA的余弦值；‎ ‎(3)求点A到平面SND的距离．‎ 解　以B为坐标原点，BC，BA为x，y轴的正方向，垂直于平面ABC的直线为z轴，建立空间直角坐标系(如图)．‎ ‎ (1)证明　由题意得A(0，4，0)，B(0，0，0)，M(1，2，1)，N(0，2，0)，S(0，4，2)，D(1，0，0)．‎ 所以：＝(－1，0，－1)，＝(0，－4，0)，·＝0，∴MN⊥AB.‎ ‎ ‎ ‎(3)∵＝(0，－2，0)，‎ ‎∴点A到平面SND的距离 d＝＝.‎ ‎14．如图，将长为4，宽为1的长方形折叠成长方体ABCD－A1B1C1D1的四个侧面，记底面上一边AB＝t(00)，P是侧棱AA1上的动点．‎ ‎(1)当AA1＝AB＝AC时，求证：A1C⊥平面ABC1；‎ ‎(2)试求三棱锥PBCC1的体积V取得最大值时的t值；‎ ‎(3)若二面角ABC1C的平面角的余弦值为，试求实数t的值．‎ ‎(1)证明　连接A1C.‎ ‎∵AA1⊥平面ABC，AB、AC⊂平面ABC，‎ ‎∴AA1⊥AC，AA1⊥AB.‎ 又AB⊥AC，‎ ‎∴以A为原点，分别以AB，AC，AA1所在直线为x轴，y轴，z轴建立如图所示的空间直角坐标系．‎ 则A(0，0，0)，C1(0，1，1)，‎ B(1，0，0)，C(0，1，0)，A1(0，0，1)，＝(0，1，－1)，＝(0，1，1)，＝(1，0，0)．‎ 设平面ABC1的法向量n＝(x，y，z)，‎ 则解得 令z＝1，则n＝(0，－1，1)．‎ ‎∵＝－n，∴A1C⊥平面ABC1.‎ ‎(2)解　∵AA1∥平面BB1C1C，‎ ‎∴点P到平面BB1C1C的距离等于点A到平面BB1C1C的距离．‎ ‎∴‎ ‎＝t2(3－2t)＝t2－t3(0