2019-2020学年江西省吉安市重点高中高二上学期第一次联考数学（理）试题 word版 8页

吉安市重点高中2020届高二年级联考 数学（理）试卷 命题人： ‎ 一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1.“”是“”的（ ）‎ ‎ A. 充分而不必要条件 B. 必要而不充分条件 ‎ ‎ C. 充分必要条件 D. 既不充分也不必要条件 ‎2．已知复数（是虚数单位），则的实部为（ ）‎ ‎ A. B． C. D． ‎ ‎3.在的展开式中，的系数是（ ）‎ ‎ A. -80 B. -10 C.5 D. 40‎ ‎4. 已知向量，，且，则实数（ ）‎ ‎ A. B. C. D. ‎ ‎5.已知函数的导函数为，且满足关系式，则 的值等于（ ）‎ ‎ A. B. C. D.‎ ‎6.空气质量指数AQI是一种反映和评价空气质量的方法，AQI指数与空气质量对应如下表所示：‎ AQI ‎0～50‎ ‎51～100‎ ‎101～150‎ ‎151～200‎ ‎201～300‎ ‎300以上 空气质量 优 良 轻度污染 中度污染 重度污染 严重污染 如图是某城市2018年12月全月的指AQI数变化统计图.‎ 根据统计图判断，下列结论正确的是（ ）‎ ‎ A. 整体上看，这个月的空气质量越来越差 ‎ B. 整体上看，前半月的空气质量好于后半月的空气质量 ‎ C. 从AQI数据看，前半月的方差大于后半月的方差 ‎ D. 从AQI数据看，前半月的平均值小于后半月的平均值 ‎ ‎7．用数学归纳法证明时，由时的假设到证明时，等式左边应添加的式子是（ ）‎ ‎ A． B．‎ ‎ C． D．‎ ‎8. 篮子里装有2个红球，3个白球和4个黑球。某人从篮子中随机取出两个球，记事件A=“‎ 取出的两个球颜色不同”，事件B=“取出一个红球，一个白球”，则( )‎ ‎ A. B. C. D.‎ ‎9. 若，，则的值为（ ）‎ ‎ A． B． C． D．‎ ‎10.“幻方”最早记载于我国公元前500年的春秋时期《大戴礼》中．“n阶幻方（n≥3，n∈N*）”是由前n2个正整数组成的—个n阶方阵，其各行各列及两条对角线所含的n个数之和（简称幻和）相等，例如“3阶幻方”的幻和为15(如图所示)．则“5阶幻方”的幻和为（ ）‎ A. 75 B. 65 C.55 D. 45‎ ‎11.双曲线的左焦点为，点A的坐标为，点P为双曲线右支上的动点，且周长的最小值为8，则双曲线的离心率为（ ）‎ ‎ A. B. C. 2 D. ‎ ‎12.己知函数与的图像上存在关于x轴对称的点，则实数a的取值范围为（ ）‎ ‎ A． B． C． D．‎ 二、填空题：本题共4小题，每小题5分，共20分。‎ ‎13. 已知，则a的值为  ．‎ ‎14. 学校要安排7位行政人员在10月1日至10月7日值班，每人值班一天，其中甲、乙二人都不安排在10月1日和2日. 不同的安排方法共有 种.（用数字作答）‎ ‎15.甲、乙、丙三位同学，其中一位是班长，一位是团支书，一位是学习委员，已知丙比学习委员的年龄大，甲与团支书的年龄不同，团支书比乙的年龄小，据此推断班长是 .‎ ‎16.把不超过实数的最大整数记为，则函数称作取整函数，又叫高斯函数，在，上任取，则的概率为 ‎ 三、解答题：(共70分。解答应写出文字说明、证明过程或演算步骤。)‎ ‎17. 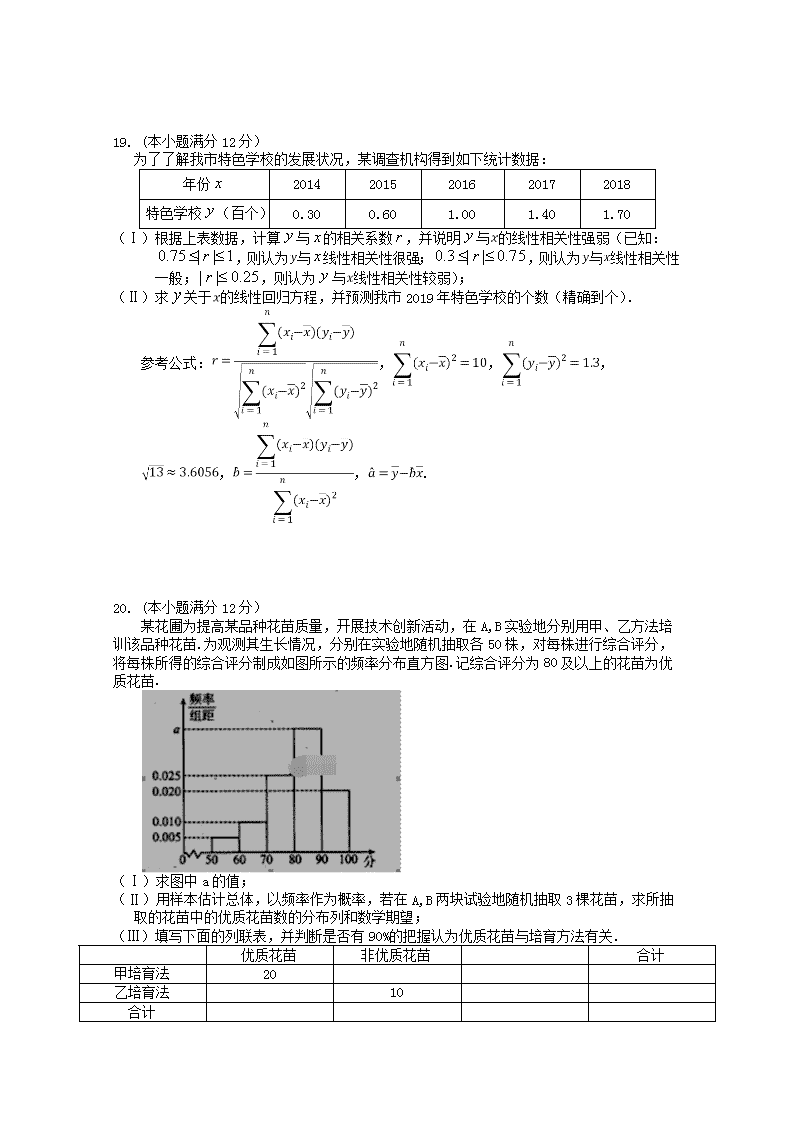(本小题满分10分）‎ 在斜中，角所对边成等差数列，且 ，‎ ‎（Ⅰ）求的大小；‎ ‎（Ⅱ）已知，求的面积．‎ ‎18.(本小题满分12分）‎ 设函数f (x) =x3 – 3ax2 + 3bx 的图象与直线12x + y –1 =0 相切于点（1,－11）．‎ ‎（Ⅰ）求a, b的值；‎ ‎（Ⅱ）讨论函数f（x）的单调性．‎ ‎19. (本小题满分12分）‎ 为了了解我市特色学校的发展状况，某调查机构得到如下统计数据：‎ 年份 ‎2014‎ ‎2015‎ ‎2016‎ ‎2017‎ ‎2018‎ 特色学校（百个）‎ ‎0.30‎ ‎0.60‎ ‎1.00‎ ‎1.40‎ ‎1.70‎ ‎（Ⅰ）根据上表数据，计算与的相关系数，并说明与的线性相关性强弱（已知：，则认为与线性相关性很强；，则认为与线性相关性一般；，则认为与线性相关性较弱）；‎ ‎（Ⅱ）求关于的线性回归方程，并预测我市2019年特色学校的个数（精确到个）．‎ 参考公式：，，，，，.‎ ‎20. (本小题满分12分）‎ 某花圃为提高某品种花苗质量，开展技术创新活动，在A,B实验地分别用甲、乙方法培训该品种花苗.为观测其生长情况，分别在实验地随机抽取各50株，对每株进行综合评分，将每株所得的综合评分制成如图所示的频率分布直方图.记综合评分为80及以上的花苗为优质花苗. ‎ ‎（Ⅰ）求图中a的值；‎ ‎（Ⅱ）用样本估计总体，以频率作为概率，若在A,B两块试验地随机抽取3棵花苗，求所抽取的花苗中的优质花苗数的分布列和数学期望；‎ ‎（Ⅲ）填写下面的列联表，并判断是否有90%的把握认为优质花苗与培育方法有关.‎ 优质花苗 非优质花苗 合计 甲培育法 ‎20‎ 乙培育法 ‎10‎ 合计 附：下面的临界值表仅供参考.‎ ‎（参考公式：，其中.）‎ ‎21. (本小题满分12分）‎ 如图，平面平面，，四边形为平行四边形，，，为线段的中点，点满足.‎ ‎（Ⅰ）求证：直线平面；‎ ‎（Ⅱ）若平面平面，求直线与平面所成角的正弦值．‎ ‎22.（本小题满分12分）‎ 已知函数.‎ ‎（Ⅰ）若在内单调递减，求实数的取值范围；‎ ‎(Ⅱ)若函数有两个极值点分别为，证明：.‎ 吉安市重点高中2020届高二年级联考 数学（理）参考答案 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 A B A D D C B B D B D C ‎13. 14. 2400 15.乙 16. ‎ ‎17.解：由 得，………2分 所以或（舍），………3分 因为，所以或，故是锐角，……………5分 （1） 成等差数列，且，所以……………6分 由余弦定理得：，所以,，……8分…………10分 ‎18.解：（Ⅰ）求导得 …………2分 ‎ 由于的图象与直线相切于点（1，－11）‎ ‎ 所以，即 …………5分 ‎ 解得 .………6分 ‎ （Ⅱ）由得 ‎ ‎ 令，解得；又令，解得………9分 ‎ 所以当时，是增函数；当时，也是增函数；但 ‎ 时，是减函数. …………12分 ‎19.解：（Ⅰ），， ………2分 ‎，…5分 ‎∴与线性相关性很强. ………6分 ‎（Ⅱ），………8分 ‎，‎ ‎∴关于的线性回归方程是. ………10分 ‎ 当时，（=0.363+1=2.08）（百个），‎ 即我市2019年特色学校的个数约为208个. ………12分 ‎20.由，‎ 解得 ………2分 由与频率分布直，优质花苗的频率为，即概率为，………3分 设所抽取的花苗为优质花苗的颗数为，则，于是，‎ 其分布列为： ………7分 所以，所抽取的花苗为优质花苗的数学期望………8分 结合与频率分布直方图，优质花苗的频率为，则样本种，优质花苗的颗数为棵，列联表如下表所示：‎ ‎………10分 可得 所以，有的把握认为优质花苗与培育方法有关系. ………12分 ‎21.（Ⅰ）证明：连接，交于点，连接 在平行四边形中，因为，‎ 所以，‎ 又因为，即，‎ 所以，‎ 又因为平面，平面，‎ 所以直线平面. ……………5分 ‎（Ⅱ）证明：因为，为线段的中点，‎ 所以，又因为平面平面于，平面 所以平面 在平行四边形中，因为，，所以 如图，以为原点，分别以所在直线为轴，轴，建立空间直角坐标系，‎ 则，因为平面 ………7分 设， 因为，‎ 设为平面的一个法向量 则不妨设 因为，‎ 设为平面的一个法向量 则不妨设 因为平面平面，所以，所以以为 所以 ………9分 所以，，‎ 所以 所以直线与平面所成角的正弦值为. ……………12分