2018届二轮复习（理）规范答题示例2　导数与不等式的恒成立问题课件（全国通用） 13页

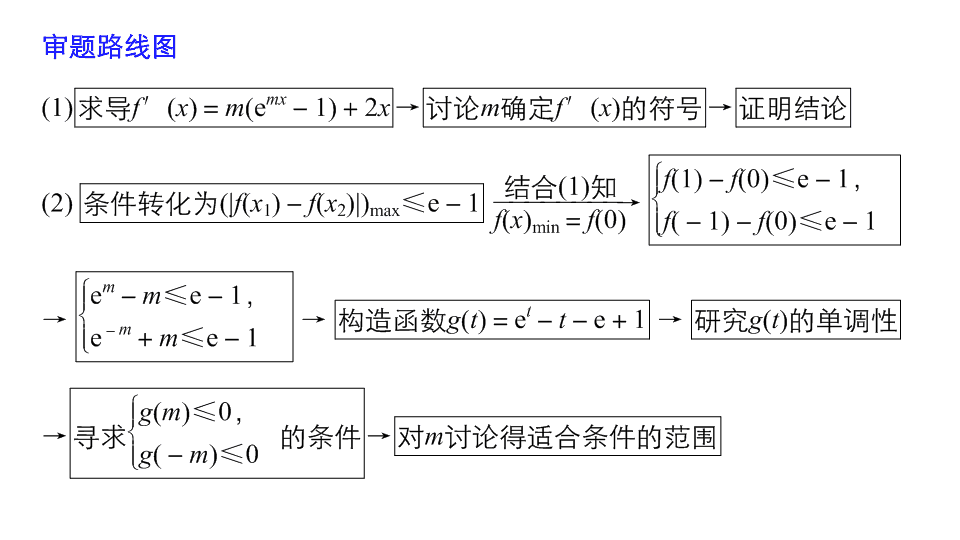
规范答题 示例 2 　 导数与不等式的恒成立问题 典例 2 　 (12 分 ) 设函数 f ( x ) ＝ e mx ＋ x 2 － mx . (1) 证明： f ( x ) 在 ( － ∞ ， 0) 上单调递减，在 (0 ，＋ ∞ ) 上单调递增； (2) 若对于任意 x 1 ， x 2 ∈ [ － 1,1] ，都有 | f ( x 1 ) － f ( x 2 )| ≤ e － 1 ，求 m 的取值 范围 . 规 范 解 答 · 分 步 得 分 (1) 证明　 f ′ ( x ) ＝ m (e mx － 1) ＋ 2 x . 1 分 若 m ≥ 0 ，则当 x ∈ ( － ∞ ， 0) 时， e mx － 1 ≤ 0 ， f ′ ( x ) ＜ 0 ； 当 x ∈ (0 ，＋ ∞ ) 时， e mx － 1 ≥ 0 ， f ′ ( x ) ＞ 0. 若 m ＜ 0 ，则当 x ∈ ( － ∞ ， 0) 时， e mx － 1 ＞ 0 ， f ′ ( x ) ＜ 0 ； 当 x ∈ (0 ，＋ ∞ ) 时， e mx － 1 ＜ 0 ， f ′ ( x ) ＞ 0 . 4 分 所以， f ( x ) 在 ( － ∞ ， 0) 上单调递减，在 (0 ，＋ ∞ ) 上单调递增 . 6 分 (2) 解　 由 (1) 知，对任意的 m ， f ( x ) 在 [ － 1,0] 上单调递减，在 [0,1] 上单调递增， 故 f ( x ) 在 x ＝ 0 处取得最小值． 所以对于任意 x 1 ， x 2 ∈ [ － 1,1] ， | f ( x 1 ) － f ( x 2 )| ≤ e － 1 的充要条件 是 设函数 g ( t ) ＝ e t － t － e ＋ 1 ，则 g ′ ( t ) ＝ e t － 1 . 9 分 当 t ＜ 0 时， g ′ ( t ) ＜ 0 ；当 t ＞ 0 时， g ′ ( t ) ＞ 0. 故 g ( t ) 在 ( － ∞ ， 0) 上单调递减，在 (0 ，＋ ∞ ) 上单调递增 . 又 g (1) ＝ 0 ， g ( － 1) ＝ e － 1 ＋ 2 － e ＜ 0 ，故当 t ∈ [ － 1,1 ] 时， g ( t ) ≤ 0. 当 m ∈ [ － 1,1] 时， g ( m ) ≤ 0 ， g ( － m ) ≤ 0 ，即 ① 式成立 ； 10 分 当 m ＞ 1 时，由 g ( t ) 的单调性，得 g ( m ) ＞ 0 ，即 e m － m ＞ e － 1 ； 当 m ＜－ 1 时， g ( － m ) ＞ 0 ，即 e － m ＋ m ＞ e － 1 . 11 分 综上， m 的取值范围是 [ － 1,1 ] . 12 分 构 建 答 题 模 板 第一步 求导数： 一般先确定函数的定义域，再求 f ′ ( x ) ． 第二步 定区间： 根据 f ′ ( x ) 的符号确定函数的单调区间． 第三步 寻条件： 一般将恒成立问题转化为函数的最值问题． 第四步 写步骤： 通过函数单调性探求函数最值，对于最值可能在两点取到的恒成立问题，可转化为不等式组恒成立． 第五步 再反思： 查看是否注意定义域、区间的写法、最值点的探求是否合理等 . 评分细则　 (1) 求出导数给 1 分； (2) 讨论时漏掉 m ＝ 0 扣 1 分；两种情况只讨论正确一种给 2 分； (3) 确定 f ′ ( x ) 符号时只有结论无中间过程扣 1 分； (4) 写出 f ( x ) 在 x ＝ 0 处取得最小值给 1 分； (5) 无最后结论扣 1 分； (6) 其他方法构造函数同样给分． 解答 (1) 求函数 f ( x ) 的单调区间和极值； x (0,1) 1 (1 ，＋ ∞ ) f ′ ( x ) ＋ 0 － f ( x ) 单调递增 极大值 单调递减 因此函数 f ( x ) 的增区间为 (0,1) ，减区间为 (1 ，＋ ∞ ) ， 极大值为 f (1) ＝ 1 ，无 极小值 . 解答 (2) 若对任意的 x >1 ，恒有 ln( x － 1) ＋ k ＋ 1 ≤ kx 成立，求 k 的取值范围 ； 解　 因为 x >1 ， 所以 f ( x － 1) max ≤ k ，所以 k ≥ 1. 证明 当且仅当 x ＝ 1 时取等号． 令 x ＝ n 2 ( n ∈ N * ， n ≥ 2) ．