高考理科数学专题复习练习10.2用样本估计总体 4页

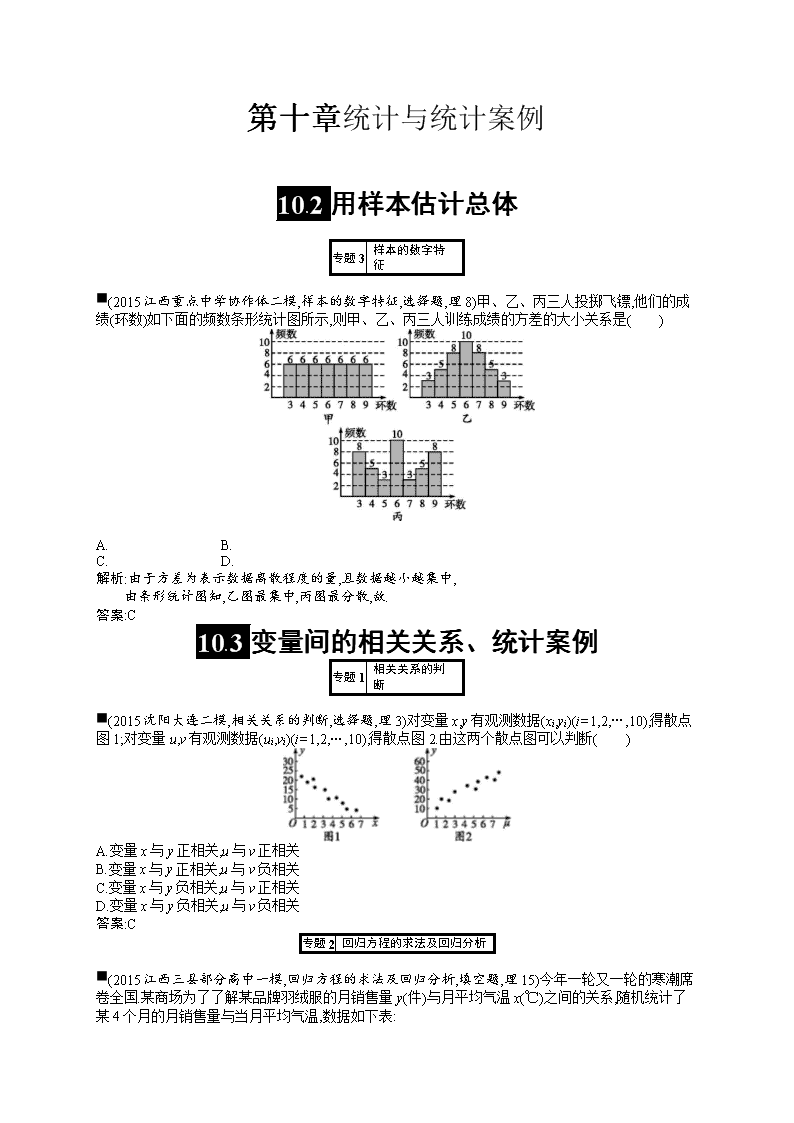
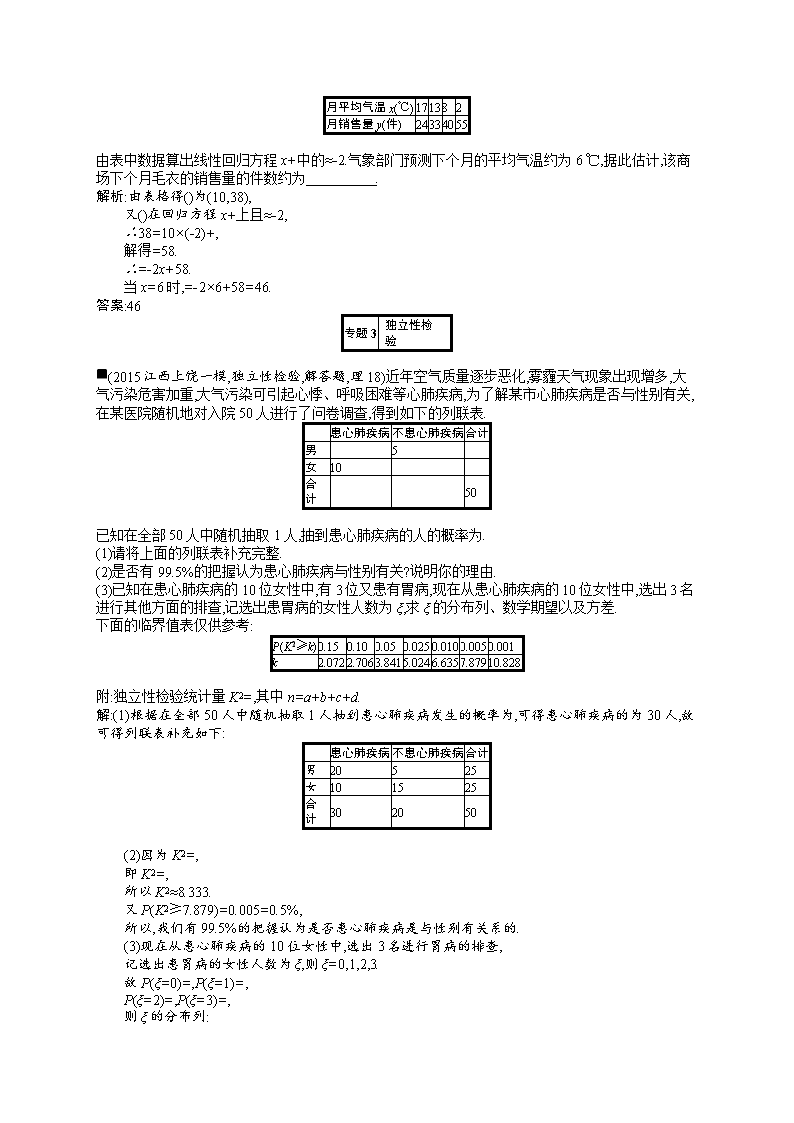
第十章统计与统计案例 ‎10.2用样本估计总体 专题3‎ 样本的数字特征 ‎■(2015江西重点中学协作体二模,样本的数字特征,选择题,理8)甲、乙、丙三人投掷飞镖,他们的成绩(环数)如下面的频数条形统计图所示,则甲、乙、丙三人训练成绩的方差的大小关系是(　　)‎ ‎　　　　　　　　　　　　　　　　‎ A. B.‎ C. D.‎ 解析:由于方差为表示数据离散程度的量,且数据越小越集中,‎ 由条形统计图知,乙图最集中,丙图最分散,故.‎ 答案:C ‎10.3变量间的相关关系、统计案例 专题1‎ 相关关系的判断 ‎■(2015沈阳大连二模,相关关系的判断,选择题,理3)对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图1;对变量u,v有观测数据(ui,vi)(i=1,2,…,10),得散点图2.由这两个散点图可以判断(　　)‎ A.变量x与y正相关,u与v正相关 B.变量x与y正相关,u与v负相关 C.变量x与y负相关,u与v正相关 D.变量x与y负相关,u与v负相关 答案:C 专题2‎ 回归方程的求法及回归分析 ‎■(2015江西三县部分高中一模,回归方程的求法及回归分析,填空题,理15)今年一轮又一轮的寒潮席卷全国.某商场为了了解某品牌羽绒服的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,数据如下表:‎ 月平均气温x(℃)‎ ‎17‎ ‎13‎ ‎8‎ ‎2‎ 月销售量y(件)‎ ‎24‎ ‎33‎ ‎40‎ ‎55‎ 由表中数据算出线性回归方程x+中的≈-2.气象部门预测下个月的平均气温约为6 ℃,据此估计,该商场下个月毛衣的销售量的件数约为　　　　　. ‎ 解析:由表格得()为(10,38),‎ 又()在回归方程x+上且≈-2,‎ ‎∴38=10×(-2)+,‎ 解得=58.‎ ‎∴=-2x+58.‎ 当x=6时,=-2×6+58=46.‎ 答案:46‎ 专题3‎ 独立性检验 ‎■(2015江西上饶一模,独立性检验,解答题,理18)近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重,大气污染可引起心悸、呼吸困难等心肺疾病,为了解某市心肺疾病是否与性别有关,在某医院随机地对入院50人进行了问卷调查,得到如下的列联表.‎ 患心肺疾病 不患心肺疾病 合计 男 ‎5‎ 女 ‎10‎ 合计 ‎50‎ 已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为.‎ ‎(1)请将上面的列联表补充完整.‎ ‎(2)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由.‎ ‎(3)已知在患心肺疾病的10位女性中,有3位又患有胃病,现在从患心肺疾病的10位女性中,选出3名进行其他方面的排查,记选出患胃病的女性人数为ξ,求ξ的分布列、数学期望以及方差.‎ 下面的临界值表仅供参考:‎ P(K2≥k)‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 附:独立性检验统计量K2=,其中n=a+b+c+d.‎ 解:(1)根据在全部50人中随机抽取1人抽到患心肺疾病发生的概率为,可得患心肺疾病的为30人,故可得列联表补充如下:‎ 患心肺疾病 不患心肺疾病 合计 男 ‎20‎ ‎5‎ ‎25‎ 女 ‎10‎ ‎15‎ ‎25‎ 合计 ‎30‎ ‎20‎ ‎50‎ ‎(2)因为K2=,‎ 即K2=,‎ 所以K2≈8.333.‎ 又P(K2≥7.879)=0.005=0.5%,‎ 所以,我们有99.5%的把握认为是否患心肺疾病是与性别有关系的.‎ ‎(3)现在从患心肺疾病的10位女性中,选出3名进行胃病的排查,‎ 记选出患胃病的女性人数为ξ,则ξ=0,1,2,3.‎ 故P(ξ=0)=,P(ξ=1)=,‎ P(ξ=2)=,P(ξ=3)=,‎ 则ξ的分布列:‎ ξ ‎0‎ ‎1‎ ‎2‎ ‎3‎ P 则Eξ=1×+2×+3×=0.9,‎ Dξ=×(0-0.9)2+×(1-0.9)2+×(2-0.9)2+×(3-0.9)2=0.49.‎ ‎■(2015江西师大附中、鹰潭一中模拟,独立性检验,解答题,理18)某大学的一个社会实践调查小组,在对大学生的良好“光盘习惯”的调査中,随机发放了120份问卷.对收回的100份有效问卷进行统计,得到如下2×2列联表:‎ 做不到光盘 能做到光盘 合计 男 ‎45‎ ‎10‎ ‎55‎ 女 ‎30‎ ‎15‎ ‎45‎ 合计 ‎75‎ ‎25‎ ‎100‎ ‎(1)现已按是否能做到光盘分层从45份女生问卷中抽取了9份问卷,若从这9份问卷中随机抽取4份,并记其中能做到光盘的问卷的份数为ξ,试求随机变量ξ的分布列和数学期望.‎ ‎(2)如果认为良好“光盘习惯”与性别有关犯错误的概率不超过P,那么根据临界值表最精确的P的值应为多少?请说明理由.‎ 附:独立性检验统计量K2=,其中n=a+b+c+d,‎ 独立性检验临界表:‎ P(K2≥k0)‎ ‎0.25‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ k0‎ ‎1.323‎ ‎2.072‎ ‎2.706‎ ‎3.840‎ ‎5.024‎ 解:(1)因为9份女生问卷是用分层抽样取到的,所以这9份问卷中有6份做不到光盘,3份能做到光盘.‎ 因为ξ表示从这9份问卷中随机抽取的4份中能做到光盘的问卷份数,所以ξ有0,1,2,3的可能取值,‎ 所以P(ξ=0)=,P(ξ=1)=,P(ξ=2)=,P(ξ=3)=.‎ ξ的分布列如下 ξ ‎0‎ ‎1‎ ‎2‎ ‎3‎ P 所以Eξ=0×+1×+2×+3×.‎ ‎(2)K2=≈3.03.‎ 因为2.706<3.03<3.840,‎ 所以能在犯错误的概率不超过0.10的前提下认为良好“光盘习惯”与性别有关,即P=0.1.‎ ‎■(2015沈阳大连二模,独立性检验,解答题,理18)某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出500件,量其内径尺寸,结果如下表:‎ 甲厂:‎ 分组 ‎[29.86,‎ ‎29.90)‎ ‎[29.90,‎ ‎29.94)‎ ‎[29.94,‎ ‎29.98)‎ ‎[29.98,‎ ‎30.02)‎ ‎[30.02,‎ ‎30.06)‎ ‎[30.06,‎ ‎30.10)‎ ‎[30.10,‎ ‎30.14)‎ 频数 ‎15‎ ‎30‎ ‎125‎ ‎198‎ ‎77‎ ‎35‎ ‎20‎ 乙厂:‎ 分组 ‎[29.86,‎ ‎29.90)‎ ‎[29.90,‎ ‎29.94)‎ ‎[29.94,‎ ‎29.98)‎ ‎[29.98,‎ ‎30.02)‎ ‎[30.02,‎ ‎30.06)‎ ‎[30.06,‎ ‎30.10)‎ ‎[30.10,‎ ‎30.14)‎ 频数 ‎40‎ ‎70‎ ‎79‎ ‎162‎ ‎59‎ ‎55‎ ‎35‎ ‎(1)由以上统计数据填下面2×2列联表,并问是否有99.9%的把握认为“生产的零件是否为优质品与不同的分厂有关”.‎ 甲厂 乙厂 合计 优质品 非优质品 合计 附:K2=‎ P(K2≥k0)‎ ‎0.100‎ ‎0.050‎ ‎0.025‎ ‎0.010‎ ‎0.001‎ k0‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎10.828‎ ‎(2)现用分层抽样方法(按优质品和非优质品分两层).从两厂中各抽取五件零件,然后从每个厂的五件产品中各抽取两件,将这四件产品中的优质品数记为X,求X的分布列.‎ 解:(1)列联表如下:‎ 甲厂 乙厂 合计 优质品 ‎400‎ ‎300‎ ‎700‎ 非优质品 ‎100‎ ‎200‎ ‎300‎ 合计 ‎500‎ ‎500‎ ‎1000‎ K2=≈47.619>10.828.‎ 所以有99.9%的把握认为“生产的零件是否为优质品与不同的分厂有关”.‎ ‎(2)甲厂有4件优质品,1件非优质品;乙厂有3件优质品,2件非优质品.‎ 从两个厂各抽取2件产品,优质品数X的取值为1,2,3,4.‎ P(X=1)=;‎ P(X=2)=;‎ P(X=4)=,‎ 所以P(X=3)=1-.‎ 所以X的分布列为 X ‎1‎ ‎2‎ ‎3‎ ‎4‎ P