广东省惠州市惠东县惠东高级中学2018-2019学年高二10月月考数学试题（答案不全） Word版含答案 6页

惠东高级中学高二年级上学期第一学段考试 数学试卷2018.10‎ 说明：‎ （1） 本卷共22题，满分150分，考试时间120分钟。‎ （2） 请看清楚各题答题位置，未在相应位置答题不得分，务必用黑色字迹的签字笔或钢笔答题。‎ （3） 请大家遵守考试规则，考出自己的真实水平，给自己、给老师做教学参考。‎ 一、选择题（每小题5分，共60分）‎ ‎1．某校数学教研组为了解学生学习数学的情况，采用分层抽样的方法从高一600人、高二780人、高三人中，抽取35人进行问卷调查，已知从高二年级抽取了13人，则＝(　　)‎ A．660　　　 B．720 C．780　　 D．800‎ ‎2.△ABC中，若c=，则角C的度数是( )‎ ‎ A.60° B.120° C.60°或120° D.45°‎ ‎3．先后抛掷质地均匀的硬币三次,则至少一次正面朝上的概率是 ( )‎ A. B. C. D. ‎ ‎4．设,则下列不等式中恒成立的是 ( )‎ ‎ A． B． C． D． ‎ ‎5.下列各数中最小的数是（ ）‎ A. B C D ‎ ‎6.在中，三边长，，，则的值等于（ ）‎ ‎ A． B． C． D．‎ ‎7.对某同学的6次数学测试成绩(满分100分)进行统计，作出的茎叶图如图所示，给出关于该同学数学成绩的以下说法：①中位数为84； ②众数为85；③平均数为85； ④极差为12.其中，正确说法的序号是（ ）‎ A. ①② B.③④ C. 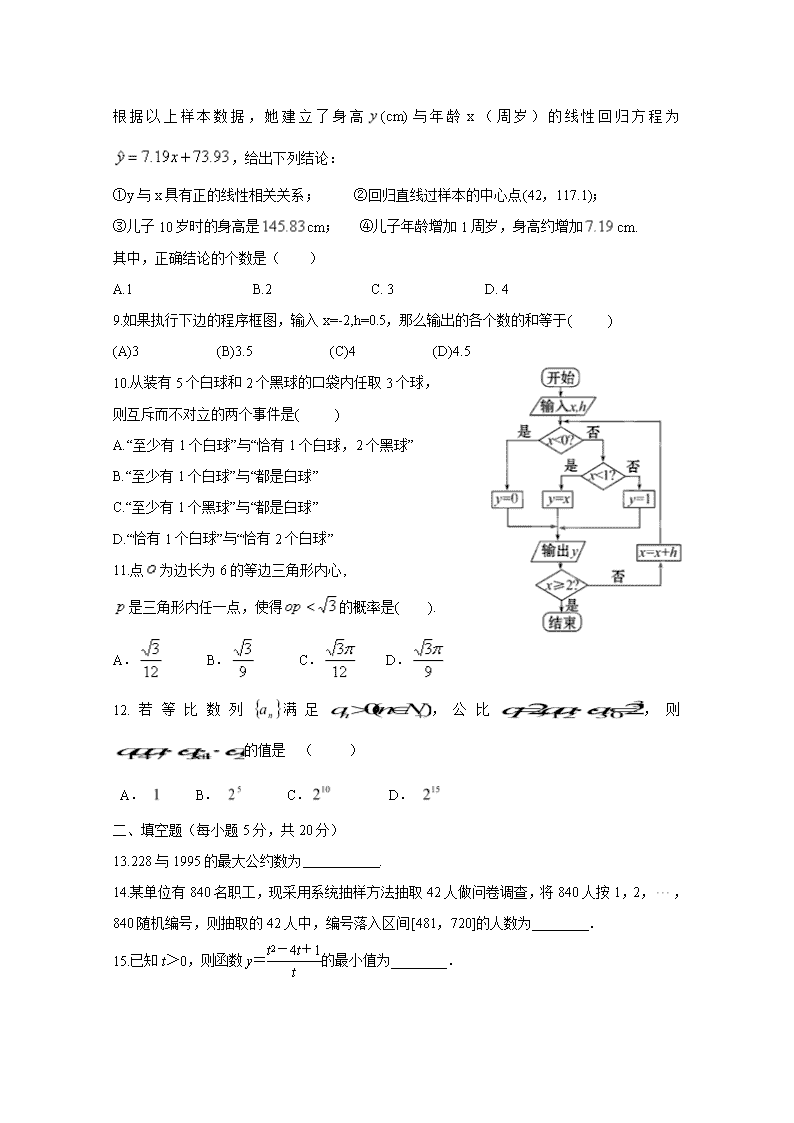②④ D.①③‎ ‎8．下表是一位母亲给儿子作的成长记录：‎ 年龄/周岁 ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ 身高/cm ‎94.8‎ ‎104.2‎ ‎108.7‎ ‎117.8‎ ‎124.3‎ ‎130.8‎ ‎139.1‎ 根据以上样本数据，她建立了身高(cm)与年龄x（周岁）的线性回归方程为，给出下列结论：‎ ‎①y与x具有正的线性相关关系； ②回归直线过样本的中心点(42，117.1)；‎ ‎③儿子10岁时的身高是cm； ④儿子年龄增加1周岁，身高约增加cm.‎ 其中，正确结论的个数是（ ）‎ A.1 B.2 C. 3 D. 4‎ ‎9.如果执行下边的程序框图，输入x=-2,h=0.5，那么输出的各个数的和等于( )‎ ‎(A)3 (B)3.5 (C)4 (D)4.5‎ ‎10.从装有5个白球和2个黑球的口袋内任取3个球，‎ 则互斥而不对立的两个事件是( )‎ A. ‎“至少有1个白球”与“恰有1个白球，2个黑球”‎ B. ‎“至少有1个白球”与“都是白球”‎ C. ‎“至少有1个黑球”与“都是白球”‎ D.“恰有1个白球”与“恰有2个白球”‎ ‎11.点为边长为6的等边三角形内心,‎ 是三角形内任一点，使得的概率是( ).‎ A． B． C． D．‎ ‎12.若等比数列满足，公比，则的值是 （ ）‎ ‎ A． B． C． D． ‎ 二、填空题（每小题5分，共20分）‎ ‎13.228与1995的最大公约数为 .‎ ‎14.某单位有840名职工，现采用系统抽样方法抽取42人做问卷调查，将840人按1，2，，840随机编号，则抽取的42人中，编号落入区间[481，720]的人数为 ． ‎ ‎15.已知t＞0，则函数y＝的最小值为________．‎ ‎16.已知数列满足，则=_____________．‎ 三、解答题（本大题共6小题，满分70分．解答应写出文字说明、证明过程或演算步骤）‎ ‎17.（本题满分10分）在锐角中，边、是方程的两根，、满足，解答下列问题：‎ ‎ （1）求角的度数；‎ ‎ （2）求边的长度；‎ ‎ （3）求的面积.‎ ‎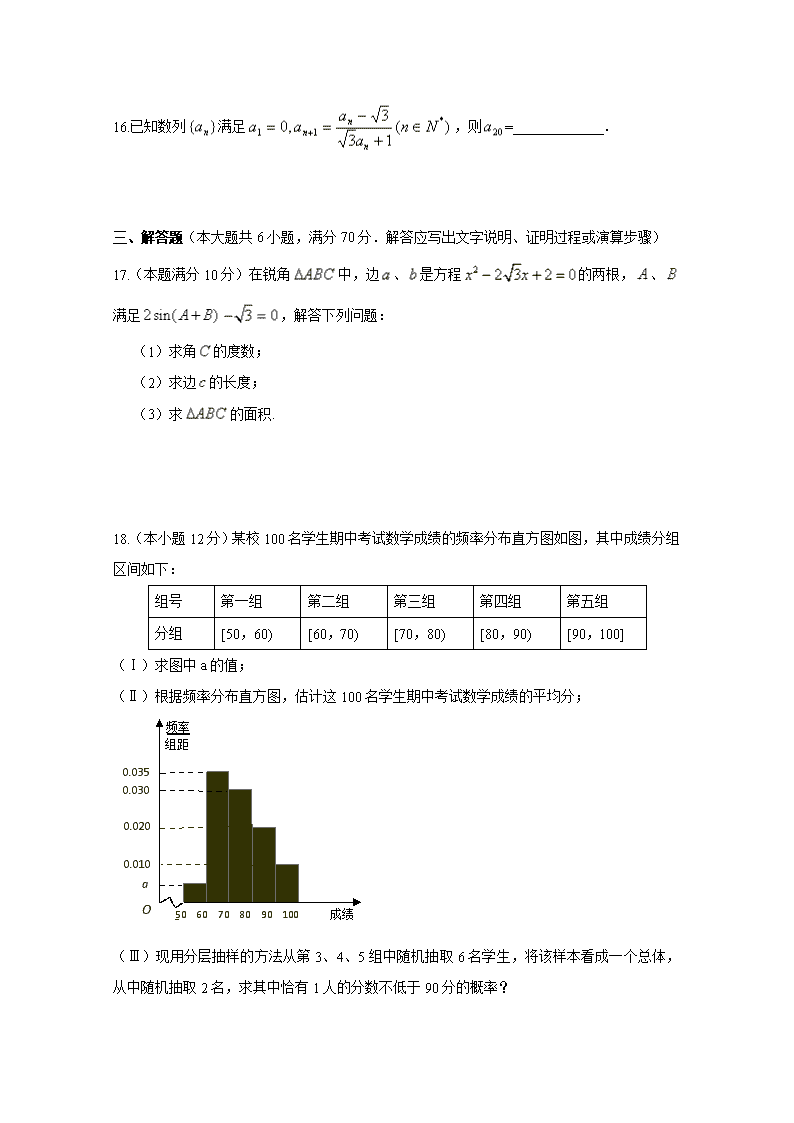18.（本小题12分）某校100名学生期中考试数学成绩的频率分布直方图如图，其中成绩分组区间如下：‎ 组号 第一组 第二组 第三组 第四组 第五组 分组 ‎[50，60)‎ ‎[60，70)‎ ‎[70，80)‎ ‎[80，90)‎ ‎[90，100]‎ ‎（Ⅰ）求图中a的值；‎ ‎（Ⅱ）根据频率分布直方图，估计这100名学生期中考试数学成绩的平均分；‎ 频率 组距 成绩 ‎_‎ ‎50 60 70 80 90 100‎ ‎0.035‎ ‎0.030‎ ‎0.020‎ ‎0.010‎ a O ‎（Ⅲ）现用分层抽样的方法从第3、4、5组中随机抽取6名学生，将该样本看成一个总体，从中随机抽取2名，求其中恰有1人的分数不低于90分的概率？‎ ‎19．（本小题12分）甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取5次，记录如下：‎ 甲 88 89 92 90 91 乙 84 88 96 89 93‎ ‎（Ⅰ）用茎叶图表示这两组数据；‎ ‎（Ⅱ）现要从中选派一人参加数学竞赛，你认为选派哪位学生参加合适？请说明理由.（用样本数据特征来说明.）‎ ‎20.（本小题12分）东海水晶制品厂去年的年产量为10万件，每件水晶产品的销售价格为100元，固定成本为80元．从今年起，工厂投入100万元科技成本．并计划以后每年比上一年多投入100万元科技成本．预计产量每年递增1万件，每件水晶产品的固定成本g(n)与科技成本的投入次数n的关系是g(n)＝.若水晶产品的销售价格不变，第 n次投入后的年利润为f(n)万元．‎ ‎(1)求出f(n)的表达式；‎ ‎(2)求从今年算起第几年利润最高？最高利润为多少万元？‎ ‎21.（本小题12分）随着我国经济的发展，居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款（年底余额）如下表：‎ 年份 ‎2010‎ ‎2011‎ ‎2012‎ ‎2013‎ ‎2014‎ 时间代号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 储蓄存款（千亿元）‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎10‎ ‎ (Ⅰ)求关于的回归方程.‎ ‎(Ⅱ)用所求回归方程预测该地区2015年（）的人民币储蓄存款.‎ 附：回归方程中 ‎22.（本题满分12分）已知函数.无穷数列满足.‎ ‎(1)若,求,,;‎ ‎(2)若,且,,成等比数列,求的值;‎ ‎(3)是否存在,使得,,,,成等差数列?若存在,求出所有这样的;若不存在,说明理由.‎ 单选1‎ B 单选2‎ B 单选3‎ D 单选4‎ C 单选5‎ A 单选6‎ D 单选7‎ D 单选8‎ B 单选9‎ B 单选10‎ D 单选11‎ D 单选12‎ A