贵州省遵义第二十一中学2018-2019高二下学期第一次月考数学（文）试卷+缺答案 4页

遵义市第二十一中学2018-2019-2第一次月考 高二数学文科试题 一、选择题（本大题共12小题，每小题5分，共计60分）‎ ‎1、已知样本，则它们的平均数为（ ）‎ A、 B、‎ C、 D、‎ ‎2、在用样本频率估计总体分布的过程中，下列说法中正确的是（ ）‎ A.总体容量越大，估计越精确 B.总体容量越小，估计越精确 C.样本容量越大，估计越精确 D.样本容量越小，估计越精确 ‎3、是的导函数，则的值是（ ）‎ A. 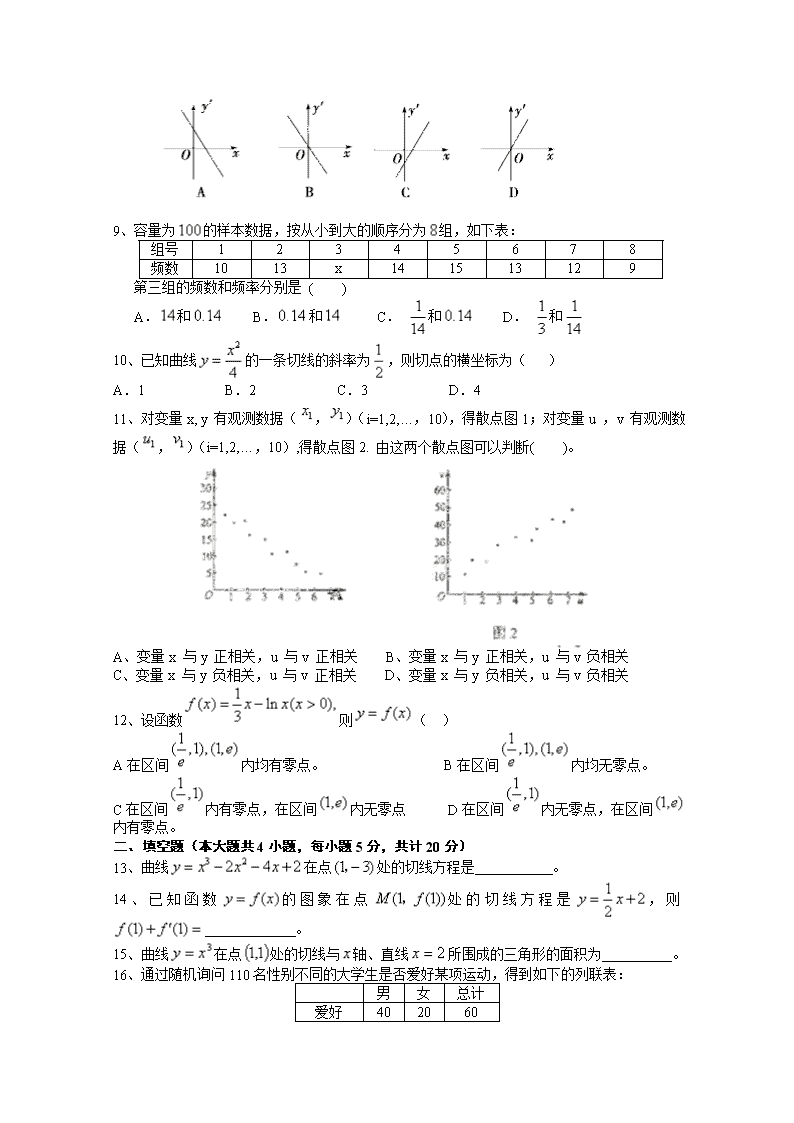B． C．3 D．4‎ ‎4、若满足，则（ ）‎ A． B． C．2 D．4‎ ‎5、函数f(x)的定义域为开区间(a，b)，导函数f′(x)在(a，b)内的图象如图所示，则函数f(x)在开区间(a，b)内有极小值点的个数为 A．1　　　B．2 C．3 D．4‎ ‎6、函数的递增区间是（ ）‎ A． B． C． D．‎ ‎7、曲线在点（1，－1）处的切线方程为 （ ）‎ ‎ A． B． C． D．‎ 8、 已知二次函数f(x)的图象如图所示，则其导函数f′(x)的图象大致形状是 ‎ ‎9、容量为的样本数据，按从小到大的顺序分为组，如下表：‎ 组号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 频数 ‎10‎ ‎13‎ x ‎14‎ ‎15‎ ‎13‎ ‎12‎ ‎9‎ 第三组的频数和频率分别是 ( )‎ A． 和 B．和 C． 和 D． 和 ‎10、已知曲线的一条切线的斜率为，则切点的横坐标为（ ）‎ A．1 B．2 C．3 D．4‎ ‎11、对变量x, y 有观测数据（，）（i=1,2,…，10），得散点图1；对变量u ，v 有观测数据（，）（i=1,2,…，10）,得散点图2. 由这两个散点图可以判断( )。‎ A、变量x 与y 正相关，u 与v 正相关 B、变量x 与y 正相关，u 与v 负相关 C、变量x 与y 负相关，u 与v 正相关 D、变量x 与y 负相关，u 与v 负相关 ‎12、设函数则（ ）‎ A在区间内均有零点。 B在区间内均无零点。‎ C在区间内有零点，在区间内无零点 D在区间内无零点，在区间内有零点。‎ 二、填空题（本大题共4小题，每小题5分，共计20分）‎ ‎13、曲线在点处的切线方程是 。‎ ‎14、已知函数的图象在点处的切线方程是，则 。‎ ‎15、曲线在点处的切线与轴、直线所围成的三角形的面积为__________。‎ ‎16、通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：‎ 男 女 总计 爱好 ‎40‎ ‎20‎ ‎60‎ 不爱好 ‎20‎ ‎30‎ ‎50‎ 总计 ‎60‎ ‎50‎ ‎110‎ 由χ2＝算得，‎ χ2＝≈7.8.‎ 附表：‎ P(χ2≥k)‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ k ‎3.841‎ ‎6.635‎ ‎10.828‎ 参照附表，得到的正确结论是________．‎ ‎①在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”；‎ ‎②在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”；‎ ‎③有99%以上的把握认为“爱好该项运动与性别有关”；‎ ‎④有99%以上的把握认为“爱好该项运动与性别无关”‎ 三、解答题（本大题共6小题，第17小题10分，其余每小题12分，共70分。解答应写出文字说明、证明过程或演算步骤）‎ ‎17、设，函数，是函数的极值点．‎ ‎（Ⅰ）求的值；（Ⅱ）求函数在区间上的最值．‎ ‎18、某城市100户居民的月平均用电量(单位：度)，以[160,180)，[180,200)，[200,220)，[220,240)，[240,260)，[260,280)，[280,300]分组的频率分布直方图如下图．‎ ‎（1）求直方图中x的值；‎ ‎（2）在月平均用电量为[220,240)，[240,260)，[260,280)，[280,300]的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在[220,240)的用户中应抽取多少户？‎ 19、 已知函数满足满足；‎ ‎（1）求的解析式（2）求的单调区间；‎ ‎20、某地区2007年至2013年农村居民家庭人均纯收入y(单位：千元)的数据如下表：‎ 年份 ‎2007‎ ‎2008‎ ‎2009‎ ‎2010‎ ‎2011‎ ‎2012‎ ‎2013‎ 年份代号t ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ 人均纯收入y ‎2.9‎ ‎3.3‎ ‎3.6‎ ‎4.4‎ ‎4.8‎ ‎5.2‎ ‎5.9‎ ‎(1)已知=0.5，求y关于t的线性回归方程 y≒t+；‎ ‎(2)利用(1)中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入．‎ 附：回归直线的斜率和截距的最小二乘估计公式分别为：‎ ‎21、为调查某地区老人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老年人，结果如下：‎ 是否需要志愿 性别 男 女 需要 ‎40‎ ‎30‎ 不需要 ‎160‎ ‎270‎ （1） 估计该地区老年人中，需要志愿者提供帮助的老年人的比例；‎ （2） 能否有99％的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？‎ 参考数据：‎ P(K2≥k)‎ ‎0.5‎ ‎0.4‎ ‎0.25‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k ‎0.455‎ ‎0.708‎ ‎1.323‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 参考公式：K2＝ ‎22.已知函数 ‎（1）求的单调减区间；（2）若在区间[－2，2].上的最大值为20，求它在该区间上的最小值.‎