高中数学第四章 3_2 简单几何体的体积 课件 15页

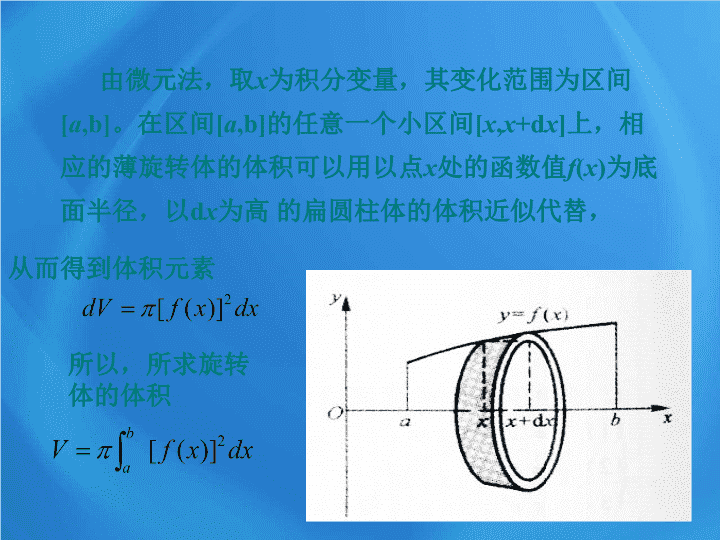
第四章 定积分 3.2 简单几何体的体积 一个平面图形绕平面内的一条定直线旋 转一周所成的立体叫 旋转体 ，这条定直线叫 做旋转轴。圆柱、圆锥、圆台、球体、球冠 都是 旋转体 。 计算由区间 [ a 、 b] 上的连续曲线 、 两直线 x = a 与 x =b 及 x 轴所围成的曲边梯形 绕 x 轴旋转一周所成的旋转体的体积 。 旋转体的体积 复习回顾   由微元法，取 x 为积分变量，其变化范围为区间 [ a ,b] 。在区间 [ a ,b] 的任意一个小区间 [ x , x +d x ] 上，相 应的薄旋转体的体积可以用以点 x 处的函数值 f ( x ) 为底 面半径，以 d x 为高 的扁圆柱体的体积近似代替，   从而得到体积元素 所以，所求旋转 体的体积     类似地可得，由区间 [c,d] 上的连续曲线 , 两直线 y=c 与 y=d 及 y 轴所围成的曲边梯形绕 y 轴旋 转一周所成的旋转体的体积为     例 1 给定直角边为 1 的等腰直角三角形，绕一条直 角边旋转一周，得到一个圆锥体 . 求它的体积 . 分析 在直角坐标系中，直角边为 1 的等腰直角三 角形可以看成是由直线 y=x ， x=1 以及 x 轴所围成的 平面图形 . 在区间 [0,1] 内插入 n-1 个分点，使 把这个三角形分割成 n 个垂直于 x 轴的小梯形，设第 I 个小梯形的宽是△ x i =x i -x i-1 ， i=1,2 ， …n ，这个小梯形 绕 x 轴旋转一周就得到一个厚度是△ x i 的小圆台当△ x i 很小时，第 i 个小圆台近似于底面半径为 x i 的小圆柱， 因此，第 i 个小圆台的体积近似为 解 圆锥的体积为 圆锥的体积就等于所有小圆台的体积和， 这个问题就是定积分问题 . 例 2 、 求由曲线 所围成的图形绕 轴旋转所得旋转体的体积。 x y o x= 1 分析： （ 1 ）分割 ; (2) 以直代曲； （ 3 ）求和； (4) 逼近。 求曲线 ，直线 ， 与 轴围成的平面图形绕 轴旋转一周所得旋 转 体的体积。 答案： 1. 练习 例 3 　求由椭圆 解 　利用图形的对称性 , 只需考虑第一象限内 ( 一 ) 绕 x 轴：选取积分变量为 x  [ 0, a ] ， 所围图形分别绕 x 轴和 y 轴旋转所成的旋转体的体积 . 任取一个子区间 [ x , x + d x ]  [ 0, a ] ， 的曲边梯形绕坐标轴旋转一周所成的旋转体的体积 ， 所求体积为该体积的 2 倍 。 在子区间 [ x , x + d x ] 上旋转体的微元为： 于是 d V 1 = p y 2 d x ， y x O x x + d x 　　 ( 二 ) 绕 y 轴： 选积分变量 y  [ 0, b ] ，任取子区间 [ y , y + d y ]  [ 0, b ]. 　　　　　　　　 　 在子区间 [ y , y + d y ] 上体积的微元为 则 y x O y + d y y x x 　　 2. 　求 y = x 2 与 y 2 = x 所围图形绕 x 轴旋转所成的旋转体体积 . 　　 解 　选积分变量 x  [ 0, 1 ] ( 两曲线的交点为 ( 0, 0 ) 和 ( 1, 1 )) ， 　任取子区间 [ x , x + d x ]  [ 0, 1 ] ， 其上的体积的微元为 x x + d x (1, 1) y 2 = x 2 y x O 练习 3. 曲线 与直线 所成的图形 的面积为 （ ） 4. 将第一象限内由 x 轴和曲线 与直线 所围成的平面图形绕 x 轴旋转一周所得旋转体的体积 等于 ( ) 练习 D C 课堂小结： 求体积的过程就是对定积分概念的进一步理解过程，总结求旋转体体积公式步骤如下： 1 ．先求出 的表达式； 2 ．代入公式 ， 即可求旋转体体积的值。