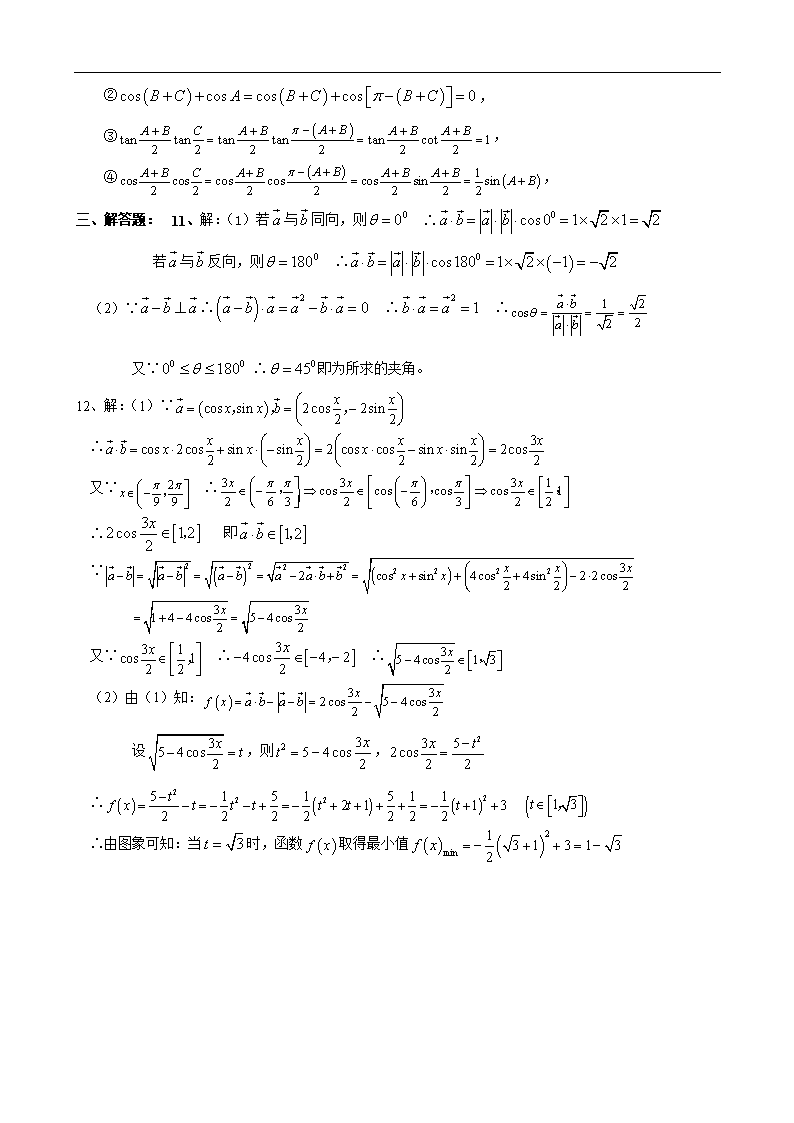高一数学必修4模块训练9答案 3页

高一数学必修4模块训练9‎ 一.选择题：‎ ‎1、的值等于( )‎ A、 B、 C、 D、‎ ‎2、在半径为的圆中，长度为2的弧所对圆心角的弧度数为( )‎ A、 B、 C、 D、 ‎ ‎3、终边落在轴上的所有角的集合可以表示为( )‎ A、 B、 ‎ C、 D、‎ ‎4、以下结论：①若，则；②若，则存在实数，使；‎ ‎③若是非零向量，，那么；④平面内任意两个非零向量都可以作为表示平面内任意一个向量的一组基底。其中正确结论的个数是( )‎ A、 B、 C、 D、‎ ‎5、若向量为两个非零向量，且，则向量与的夹角为( )‎ A、 B、 C、 D、‎ ‎6、已知A、B、C三点共线，且A、B、C三点的纵坐标分别为2、5、10，则点A分所成的比为( )‎ A、 B、 C、 D、‎ ‎7、O是平面上一定点，A、、B、C是平面上不共线的三点，动点P满足：，‎ ‎，则P的轨迹一定通过的 ( )‎ A、外心 B、内心 C、重心 D、垂心 ‎8、将函数的图象F沿轴向左平移3个单位，再沿轴向上平移2的单位后得的图象，则 ( ) ‎ A、 B、 C、 D、 ‎ 二.填空题：‎ ‎9、已知，且，则向量的坐标为_______.‎ ‎10、在中，下列三角表达式：①，②，‎ ‎③，④，其中恒为定值的有_____________（请将你认为正确的式子的序号都填上）.‎ 三．解答题：‎ ‎ 11、已知，（1）若，求；（2）若与垂直，求与的夹角。‎ ‎12. 已知向量，且，‎ ‎ 求：（1）和的取值范围；‎ ‎ （2）函数的最小值。‎ 参考答案 一、选择题：‎ CCCBBCBD ‎ 二、填空题：‎ ‎9、解：取O点为坐标原点，则由，得D点为：‎ ‎，又知故向量 ‎10、解：在中由知其中恒为定值的有：②、③‎ ‎①，‎ ‎②，‎ ‎③，‎ ‎④，‎ 三、解答题： 11、解：（1）若与同向，则 ∴‎ ‎ 若与反向，则 ∴‎ ‎ （2）∵∴ ∴ ∴‎ 又∵ ∴即为所求的夹角。‎ ‎12、解：（1）∵‎ ‎∴‎ 又∵ ∴‎ ‎∴ 即 ‎∵‎ 又∵ ∴ ∴‎ ‎（2）由（1）知：‎ 设，则，‎ ‎∴ ‎ ‎∴由图象可知：当时，函数取得最小值 ‎ ‎