【数学】2019届一轮复习人教A版 概率与统计 学案 10页

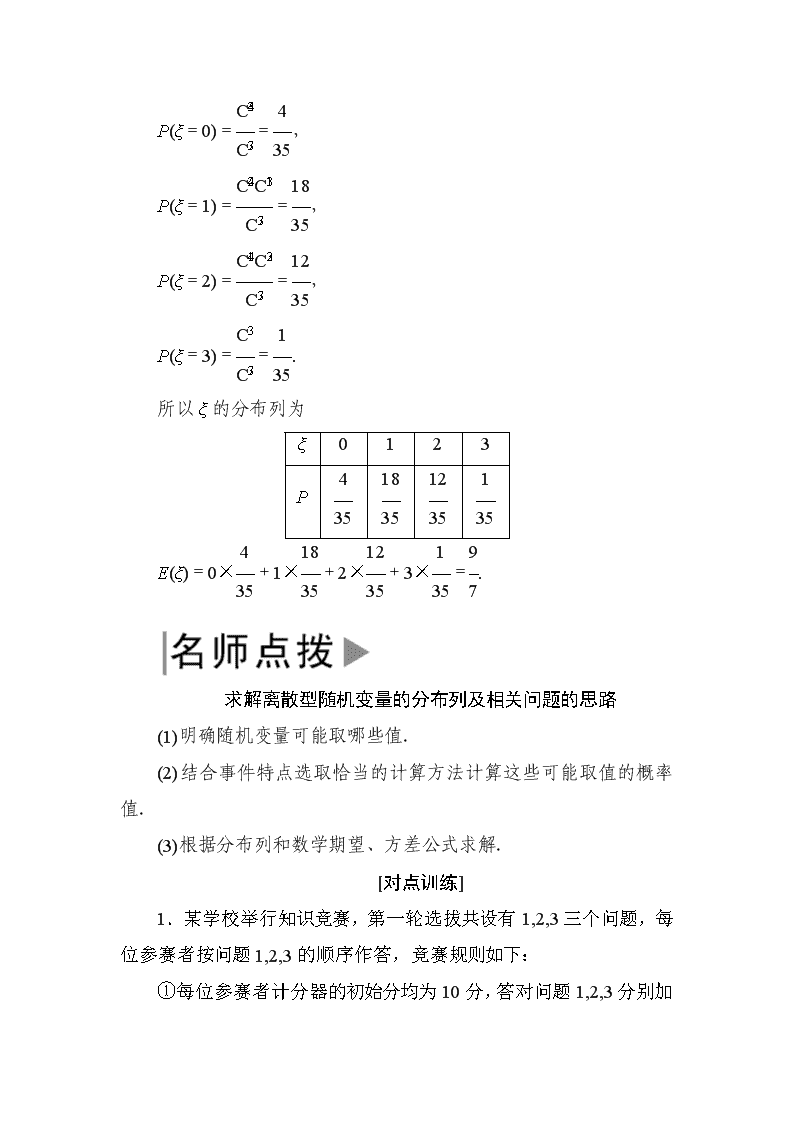
专题六 概率与统计、算法、复数、推理与证明 高考解答题专讲(六) 概率与统计 一、离散型随机变量的均值与方差 ‎ 在解决离散型随机变量的均值与方差的问题时，要善于将复杂事件分解为较简单事件，对照相关概率类型，如互斥事件类型、相互独立事件类型、古典概型等，然后用相关公式求解．‎ ‎[思维流程] ‎ ‎(1)→―→ ‎(2)→→→ ‎[解] (1)记“这3类节目各被抽到1个”为事件A，‎ 由分步乘法计数原理可得，3类节目各抽取1个的事件数为CCC＝12，事件总数为C＝35，则P(A)＝.‎ ‎(2)ξ的所有可能取值为0,1,2,3，‎ P(ξ＝0)＝＝，‎ P(ξ＝1)＝＝，‎ P(ξ＝2)＝＝，‎ P(ξ＝3)＝＝.‎ 所以ξ的分布列为 ξ ‎0‎ ‎1‎ ‎2‎ ‎3‎ P E(ξ)＝0×＋1×＋2×＋3×＝.‎ ‎ 求解离散型随机变量的分布列及相关问题的思路 ‎(1)明确随机变量可能取哪些值．‎ ‎(2)结合事件特点选取恰当的计算方法计算这些可能取值的概率值．‎ ‎(3)根据分布列和数学期望、方差公式求解．‎ ‎ [对点训练]‎ ‎1．某学校举行知识竞赛，第一轮选拔共设有1,2,3三个问题，每位参赛者按问题1,2,3的顺序作答，竞赛规则如下：‎ ‎①每位参赛者计分器的初始分均为10分，答对问题1,2,3分别加1分，2分，3分，答错任一题减2分；‎ ‎②‎ 每回答一题，积分器显示累计分数，当累计分数小于8分时，答题结束，淘汰出局；当累计分数大于或等于12分时，答题结束，进入下一轮；当答完三题，累计分数仍不足12分时，答题结束，淘汰出局．‎ 已知甲同学回答1,2,3三个问题正确的概率依次为，，，且各题回答正确与否相互之间没有影响．‎ ‎(1)求甲同学能进入下一轮的概率；‎ ‎(2)用X表示甲同学本轮答题结束时的累计分数，求X的分布列和数学期望．‎ ‎[解] (1)设事件A表示“甲同学问题1回答正确”，事件B表示“甲同学问题2回答正确”，事件C表示“甲同学问题3回答正确”，依题意得P(A)＝，P(B)＝，P(C)＝.‎ 记“甲同学能进入下一轮”为事件D，则 P(D)＝P(AC＋AB＋BC)‎ ‎＝P(AC)＋P(AB)＋P(BC)‎ ‎＝P(A)P()P(C)＋P(A)P(B)＋P()P(B)P(C)‎ ‎＝××＋×＋××＝.‎ ‎(2)X可能的取值是6,7,8,12,13.‎ P(X＝6)＝P()＝×＝，‎ P(X＝7)＝P(A)＝××＝，‎ P(X＝8)＝P(B)＝××＝，‎ P(X＝12)＝P(AC)＝××＝，‎ P(X＝13)＝P(AB＋BC)＝P(AB)＋P(BC)＝×＋××＝.‎ 所以X的分布列为 X ‎6‎ ‎7‎ ‎8‎ ‎12‎ ‎13‎ P X的数学期望E(X)＝6×＋7×＋8×＋12×＋13×＝.‎ 二、线性回归分析与独立性检验 ‎1．在分析两个变量的相关关系时，可根据样本数据作出散点图来确定两个变量之间是否具有相关关系，若具有线性相关关系，则可通过线性回归方程估计和预测变量的值．‎ ‎2．独立性检验的关键是根据2×2列联表准确计算出K2，再做判断．‎ ‎[思维流程] →→→ ‎[解] (1)记“至少有一个大于600”为事件A，‎ 则P(A)＝1－＝.‎ ‎(2)由题中表格可知，＝＝556，＝＝600.‎ ‎∴＝‎ ‎＝＝0.3，‎ ＝－＝600－0.3×556＝433.2，‎ ‎∴线性回归方程为＝0.3x＋433.2.‎ 当x＝570时，＝0.3×570＋433.2＝604.2，‎ 故特征量x为570时，特征量y的估计值为604.2.‎ ‎ 线性回归分析与独立性检验的计算 ‎(1)由回归方程分析得出的数据只是预测值不是精确值，此类问题的易错点是方程中的计算，代入公式计算要细心．‎ ‎(2)独立性检验是指利用2×2列联表，通过计算随机变量K2来确定在多大程度上两个分类变量有关系的方法．‎ ‎ [对点训练]‎ ‎2．(2017·内蒙古包头十校联考)‎‎2016年1月1日 起全国统一实施全面的两孩政策，为了解适龄民众对放开生育二胎政策的态度，某市选取70后80后作为调查对象，随机调查了100人并对调查结果进行统计，70后不打算生二胎的占全部调查人数的15 ,80后打算生二胎的占全部被调查人数的45 ,100人中共有75人打算生二胎．‎ ‎(1)根据调查数据，判断是否有90 以上把握认为“生二胎与年龄有关”，并说明理由；‎ ‎(2)以这100人的样本数据估计该市的总体数据，且以频率估计概率，若从该市70后公民中(人数很多)随机抽取3位，记其中打算生二胎的人数为X，求随机变量X的分布列，数学期望E(X)和方差D(X)．‎ 参考公式：‎ P(K2≥k)‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎(K2＝，其中n＝a＋b＋c＋d)‎ ‎[解] (1)由题意得年龄与生二胎的列联表为：‎ 生二胎 不生二胎 总计 ‎70后 ‎30‎ ‎15‎ ‎45‎ ‎80后 ‎45‎ ‎10‎ ‎55‎ 总计 ‎75‎ ‎25‎ ‎100‎ 所以K2＝＝>2.706，‎ 所以有90 以上把握认为“生二胎与年龄有关”．‎ ‎(2)由已知得该市70后“生二胎”的概率为＝，且X～B，‎ 所以P(X＝k)＝Ck3－k(k＝0,1,2,3)．‎ 故X的分布列为：‎ X ‎0‎ ‎1‎ ‎2‎ ‎3‎ P 所以E(X)＝3×＝2，方差D(X)＝3××＝.‎ 热点课题25 概率与统计的交汇问题 ‎ [感悟体验]‎ ‎ (2017·福州质检)某学校为鼓励家校互动，与某手机通讯商合作，为教师办理流量套餐．为了解该校教师手机流量使用情况，通过抽样，得到100位教师近2年每人手机月平均使用流量L(单位：M)的数据，其频率分布直方图如下：‎ 若将每位教师的手机月平均使用流量分别视为其手机月使用流量，并将频率视为概率，回答以下问题．‎ ‎(1)从该校教师中随机抽取3人，求这3人中至多有1人手机月使用流量不超过300M的概率；‎ ‎(2)现该通讯商推出三款流量套餐，详情如下：‎ 套餐名称 月套餐费/元 月套餐流量/M A ‎20‎ ‎300‎ B ‎30‎ ‎500‎ C ‎38‎ ‎700‎ 这三款套餐都有如下附加条款：套餐费月初一次性收取，手机使用流量一旦超出套餐流量，系统就自动帮用户充值200 M流量，资费20元；如果又超出充值流量，系统就再次自动帮用户充值200 M流量，资费20元，以此类推，如果当月流量有剩余，系统将自动清零，无法转入次月使用．‎ 学校欲订购其中一款流量套餐，为教师支付月套餐费，并承担系统自动充值的流量资费的75 ，其余部分由教师个人承担，问学校订购哪一款套餐最经济？说明理由．‎ ‎[解] (1)记“从该校随机抽取1位教师，该教师手机月使用流量不超过300 M”为事件D.依题意，P(D)＝(0.0008＋0.0022)×100＝0.3.‎ 从该校教师中随机抽取3人，设这3人中手机月使用流量不超过300 M的人数为X，‎ 则X～B(3,0.3)，‎ 所以从该校教师中随机抽取3人，至多有1人手机月使用流量不超过300 M的概率为P(X＝0)＋P(X＝1)＝C×0.30×(1－0.3)3＋C×0.3×(1－0.3)2＝0.343＋0.441＝0.784.‎ ‎(2)依题意，从该校随机抽取1位教师，该教师手机月使用流量L∈(300,500]的概率为(0.0025＋0.0035)×100＝0.6，L∈(500,700]的概率为(0.0008＋0.0002)×100＝0.1.‎ 当学校订购A套餐时，设学校为1位教师承担的月费用为X1元，则X1的所有可能取值为20,35,50，且P(X1＝20)＝0.3，P(X＝35)＝0.6，P(X1＝50)＝0.1，‎ 所以X1的分布列为 X1‎ ‎20‎ ‎35‎ ‎50‎ P ‎0.3‎ ‎0.6‎ ‎0.1‎ 所以E(X1)＝20×0.3＋35×0.6＋50×0.1＝32(元)．‎ 当学校订购B套餐时，设学校为1位教师承担的月费用为X2元，‎ 则X2的所有可能取值为30,45，且P(X2＝30)＝0.3＋0.6＝0.9，P(X2＝45)＝0.1，‎ 所以X2的分布列为 X2‎ ‎30‎ ‎45‎ P ‎0.9‎ ‎0.1‎ 所以E(X2)＝30×0.9＋45×0.1＝31.5(元)．‎ 当学校订购C套餐时，设学校为1位教师承担的月费用为X3元，‎ 当X3的所有可能取值为38，且P(X3＝38)＝1，所以E(X3)＝38×1＝38(元)．‎ 因为E(X2)